《 管理信息系统》| “朝闻道”知识分享大赛

[Thomas Wade]

这是我参加朝闻道知识分享大赛的第 40 篇文章

专家系统与决策支持系统的区别

区别 ：DSS强调在大范围内支持决策者工作，它可按照人的思维规律引导用户解决问题，强调的是通用性；ES强调在某较窄范围内代替决策者工作，强调专业性； DSS不可能将解决问题的过程完全自动化，即在解决问题的过程中对某些不能解决的仍需要人脑解决，人机是密切配合的;专家系统除了要求用户回答问题、提供必要数据外，基本是自动独立工作的。

知识库与推理机

规则知识集 ：描述和解决各种不同的灵活的实际问题； 把规则知识集中的所有规则连成一棵“与或”推理树（知识树），即这些规则知识集之间是有关联的。

推理树： 按逆向推理思想把知识库所含的总目标（它是某些规则的结论）作为根结点，按规则的前提和结论展开成一棵树的形式。这棵树一般称为推理树或知识树，它把知识库中的所有规则都连接起来。

专家系统的应用

医疗诊断系统MYCIN ： 医疗诊断系统MYCIN是一个用于诊断和治疗细菌感染血液病的专家咨询系统，该系统包含约450条关于细菌血液感染的诊疗规则，可以识别大约100种细菌。系统可以根据事先提供的数据和向内科医生询问得到的数据，利用系统中的诊断规则，给出诊断和治疗方面的咨询性建议。经测评，它的表现被评价为等同于人类专家，该系统足以作为临床医生的实际助手，同时被应用到医学教学上。

（三）遗传算法

将遗传算法类比“鲨鱼繁衍”案例

通过一个简单的类比“鲨鱼繁衍”的例子迁移介绍遗传算法

遗传算法的特点 ：

遗传算法是计算过程系列，概念上遵循生物进化过程的步骤。该方法通过产生后代（新的可行解决方案收集）来改善解决方案，使用当代最好的解决方案作为“父母”；

遗传算法是人工智能领域中机器学习方法的一部分，因为它们不能保证真正的最优解，遗传算法被认为是启发式方法；

遗传算法展示以多种方式自我组织和适应，生物有机体遵循进化规则——适者生存。

遗传算法的术语

染色体 ：基因串描述备选的方案

适应函数： 衡量目标（最大或最小）

交叉

父	0	3	0	6	7
母	8	6	9	3	2
子	0	3	0	3	2

交叉： 交叉的过程需要从上一代的染色体中寻找两条染色体，一条是父亲，一条是母亲。然后将这两条染色体的某一个位置切断，并拼接在一起，从而生成一条新的染色体。

突变： 突变是一个在染色体中任意的（最小）变化。它通常是用来防止算法陷入局部最优。

遗传算法的工作流程

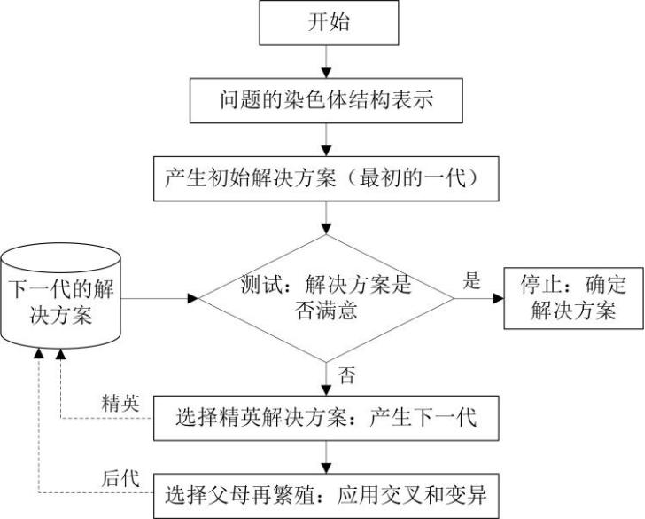
 初态用一串1和0用于表示决策变量，代表潜在解决问题办法的集合； 接下来，决策变量数学和/或象征性地汇集成一个适应度函数； 应用适应度函数和所有决策变量的约束，计算是否一个解决方案是可行的； 通过交叉和变异，生成新的染色体； 重复第三步直至解决方案满达到意。

遗传算法的优缺点

优点： 遗传算法是以决策变量的编码作为运算对象，可以直接对集合、序列、矩阵、树、图等结构对象进行操作； 仅使用适应度函数值来度量个体的优良程度，不涉及目标函数值求导求微分的过程； 具有群体搜索的特性； 遗传算法基于概率规则，而不是确定性规则； 可扩展性强。

缺点： 不具有普适性； 遗传算法的开发和结果解释需要个具有在使用遗传算法所要求的统计/编程和数学技能方面的专家； 人口聚集时，遗传算法继续寻找更好解决方案的能力实际被消除； 大多数遗传算法依赖于随机数发生器，每次运行模型产生不同的结果 为一个特定的问题定位好变量是困难的工作，同样需要获得数据来填充变量。

（四）智能代理（Intelligent Agents，IA）

智能代理的特点

知识、目标和能力是Agent本身具有的三个要素 知识是Agent对其周围环境和要求解的问题的某种描述； 目标是Agent解决问题所能达到的程度； 能力是Agent自身具有的解决问题的技能。

Agent的研究主要有智能型Agent研究、多Agent研究和面向Agent的程序设计研究三个方面。

（五）神经网络

---神经网络的概念 ---

神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆； 网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

---神经网络的功能 ---

联想记忆功能 ：神经网络通过预先存储信息和学习机制进行自适应训练，可以从不完整的信息和噪声干扰中恢复原始的完整的信息。

分类与识别功能

优化计算功能： 优化计算是指在已知的约束条件下，寻找一组参数组合，使该组合确定的目标函数达到最小。

非线性映射功能： 设计合理的神经网络通过对系统输入输出样本进行训练学习，从理论上讲，能够以任意精度逼近任意复杂的非线性函数。神经网络的这一优良性能使其可以作为多维非线性函数的通用数学模型。