北航计算机学院面向对象 2025 第一单元总结博客

赵骥远-23371524 2025-03-20 17:01:46

北航计算机学院面向对象 2025 第一单元总结博客

本篇博客是对面向对象第一单元整体的回顾与总结，旨在客观评价自己的代码架构、在作业中的表现、需要改进增强的地方等，以发挥作业的锻炼作用，更好的提升自己的代码能力。本篇博客均为个人原创，如有不足欢迎大家斧正。

1. 基于度量来分析自己的程序结构

通过度量程序类的个数、属性个数、方法个数、方法规模、分支个数等标准，可以有效反映程序设计的优良好坏，自检代码风格，明确哪些部分是值得保留的，哪些部分是冗余的，进而打磨代码经验，增强设计能力。

1.1 作业类图

类个数：经过三次作业迭代后，程序共含有17个类、1个接口。其UML大致框架如下：

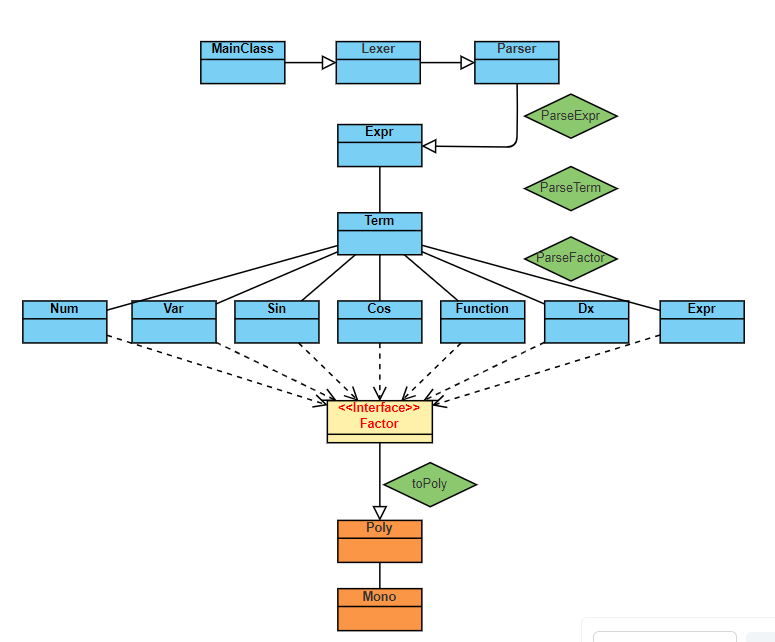
整体流程为：通过 MainClass 读入输入，利用 Lexer 根据词法解析输入，最后把解析好的 Tokens 交给 Parser 去进行语法解析。Parser 调用 ParseExpr() 方法最终返回 Expr；Expr 由 Term 构成，通过调用 ParseTerm() 方法返回 Term；Term 又由 Factor 组成（包括Num，Var，Sin，Cos，Function，Dx，Expr），通过调用 ParseFactor() 方法返回 Factor；这些因子都调用了 Factor 接口，并实现了 ToPoly() 方法。最终计算时，需要把整个表达式都转成多项式，这里依然用到递归转换。 Factor 调用 ToPoly() 方法即可转多项式；Term 需要把其中的 Factor 都转成多项式并相乘，即可得到自己的多项式；Expr 需要把其中的 Term 都转多项式并相加，即可得到表达式的多项式。最后调用 toString() 方法输出。除此以外，还有 FunctionDefiner 类，用来预处理自定义函数；Preprocessing 类，用来预处理输入字符串；Simplification 类，用来化简最后的输出；以及 Token 类，用来配合 Lexer 进行词法解析。

每个类的设计考虑：

MainClass：处理程序主要流程，依次进行输入、预处理、词法分析、语法分析、转多项式、化简、输出。
Lexer：用来从输入中按词法提取出 Token，便于后于语法分析。
Token：用来规定最小词法分割单元，作为 Lexer 的最小处理单元。
Parser：语法解析器，用来将 Lexer 分割的 Token 解析成表达式、项、因子结构。
Expr：表达式兼子表达式类，用来表示表达式结构，内部包含 Term，具有 ToPoly() 方法。
Term：项类，用来表示项结构，内部包含 Factor，具有 ToPoly() 方法。
Factor：Factor 接口，用来行为层次抽象因子，内部具有抽象的 ToPoly() 方法，方便统一管理因子。
Num：数字因子，用 BigInteger 存储数字大小。
Var：幂函数因子，存储 x 和它的幂指数。
Sin：正弦函数因子，存储内部因子和它的幂指数。
Cos：余弦函数因子，存储内部因子和它的幂指数。
Function：自定义函数因子，接受实参，并根据函数类型进行参数替换，最后解析返回Expr。
Dx：求导因子，接受表达式并解析。
Poly：多项式类，用来保存一个由多个单项式组成的多项式，可以进行乘法、加法、乘方运算。有 toString() 方法，用来输出。
Mono：单项式类，用来保存一个由常熟系数、幂函数、正弦函数、余弦函数组成的单项式。有 toString() 方法，用来输出。
FunctionDefiner：函数构建类，用来预处理构建函数，支持替换形参，保存原函数。
Preprocessing：输入预处理类，用来预处理输入字符串，去掉空白符，处理连续符号等。
Simplification：化简类，用来实现三角函数化简，简化输出。

优点：

‘1. 解析结构清晰：表达式——项——因子结构清晰，有层次条理，递归下降时方便解析。同时因子接口通过行为抽象聚合了很多不同的因子，使得程序在增加更多因子时可迭代性强，只需要新增特定因子的解析方式和 toPoly() 方法即可，整体框架无需调整。

‘2. 统一计算方法：在解析完成后，程序的所有计算过程都是基于多项式 Poly 的计算过程。因此只需要设计两部分即可。第一部分是Expr、Term、Factor 如何转换成 Poly 的方法，第二部分是 Poly 之间做乘法、加法、乘方运算的方法。这两部分相对独立，互不影响。如果有新增因子，只需要针对新因子设计 toPoly() 方法即可，无需更改 Poly 的运算方法，这有效分割了代码的各部分功能，彼此不干扰，增强了代码的可迭代性和可维护性。

‘3. 化简性能较高：在最后的化简阶段，我采用了在 Expr 调用 toPoly() 方法的时候进行化简。具体方法为：在对表达式底数进行 toPoly 操作后，先去除系数为0的单项式，之后进行一次化简操作；然后根据表达式指数进行乘方运算，并对计算结果再次重复上述操作。这样做的好处是可以保证每一处Expr转成的Poly都是最简形式，从而方便后续运算、比较、求导、输出等等。同时对于三角函数化简，我也采用了多种常见的化简方式，例如：sin(0)=0，cos(0)=1，sin((-x))=-sin(x)，cos((-x))=cos(x)，sin(x)^2+cos(x)^2=1，cos(x)^2-sin(x)^2=cos((2*x))，sin(x)*cos(x^2)+cos(x)*sin(x^2)=sin((x+x^2))等，这些化简可以有效减少多项式的项数，从而进行轻量化。

’4. 函数处理简便：函数处理采用了在原函数字符串中，通过形参的比对，来进行字符串替换实参，最终得到字符串并进行解析的方案。这种方案的好处是处理复杂度仅与原函数字符串长度有关，是O(n)的复杂度，与遍历表达式树相比不会因为内部结构的复杂而增量。

缺点：

‘1. 幂函数不支持扩展：在我的架构中，幂函数默认是 x，该类中有一个指数因子，该因子默认是 x 的指数。这种做法在幂函数仅有 x 的时候是很方便的，但是一旦幂函数不只有 x，比如扩展到 x、y、z等，就需要重构。因此这个架构可迭代性很差，在一开始设计的时候没有考虑好，是需要避免的问题。

’2. 自定义函数传参使用字符串：在实参很简单的时候，这样做是比较省时省力的方式，因为对简单的实参进行 toPoly 和 toString 操作都很容易，字符串替换后整体长度也不会很长。但是如果实参很复杂，本身就是一个很长的表达式或因子，如果采取字符串替换的方式，需要先对实参进行 toPoly，然后再对这个很长的 Poly 进行 toString 操作，替换后整个函数表达式会变得特别长，再解析会浪费很多时间；而如果将实参整体以一个因子的形式进行因子层级的替换，则时间开销是稳定的，无论这个因子有多庞大。同时以因子为单位去替换也符合程序设计的思想，并非所有情况都能用字符串解决。

'3. 多项式比较操作复杂：在比较两个 Poly 是否相同时，我采用了逐项比较的方式，这种方式虽然保证了正确性，但是因为方式很暴力很冗余，导致平均复杂度是 O(n^2)。可以采用效率更高的 Hash 方法来进行比较，通过重写 Hashcode 和 equals 方法，可以高效比较两个单项式或多项式是否相等。但这种方式要求对 Hashcode 和 equals 方法有较深的理解，有做错的风险。

1.2 作业度量

作业度量将从类代码行数、类代码复杂度、类方法复杂度等方面度量代码的可读性、可维护性、可迭代性，从而总结值得保留的方面，规避不好的设计，为今后的代码设计优化思路。

本次作业所有类的总代码行数如下图所示：

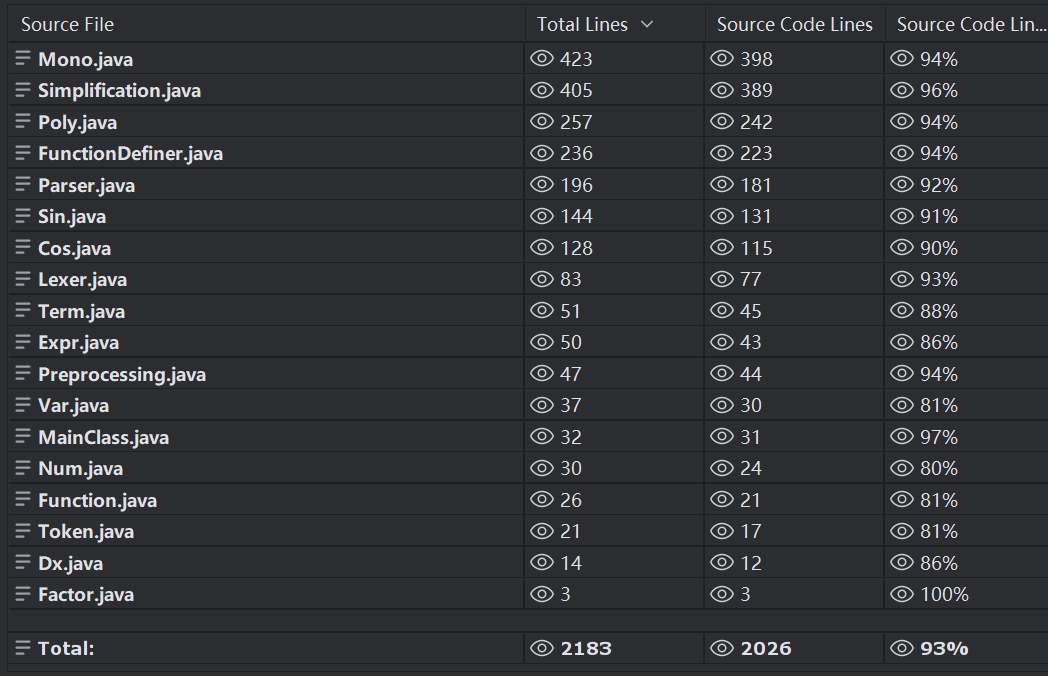
可以看出，代码总行数为2183行，代码量整体适中稍微偏多。各个类代码行数整体分为三档：较少、适中、较多。代码行数较少的类平均为50行，主要为 Factor 类，用来定义 Factor 的成员变量和 toPoly 方法。代码行数适中的类平均为200行，一般为具有一定功能和复杂方法的类，例如 Parser 类、Sin 类、Cos 类、FunctionDefiner 类、Poly 类等。代码行数较多的类平均为400行，一般为具有强大功能重要作用的类，具有很多复杂方法，例如 Mono 类、Simplification 类。代码行数分配整体较为平均合理，有详略之分。

除了代码行数，还可以通过方法复杂度、类复杂度来度量代码，如下图所示：

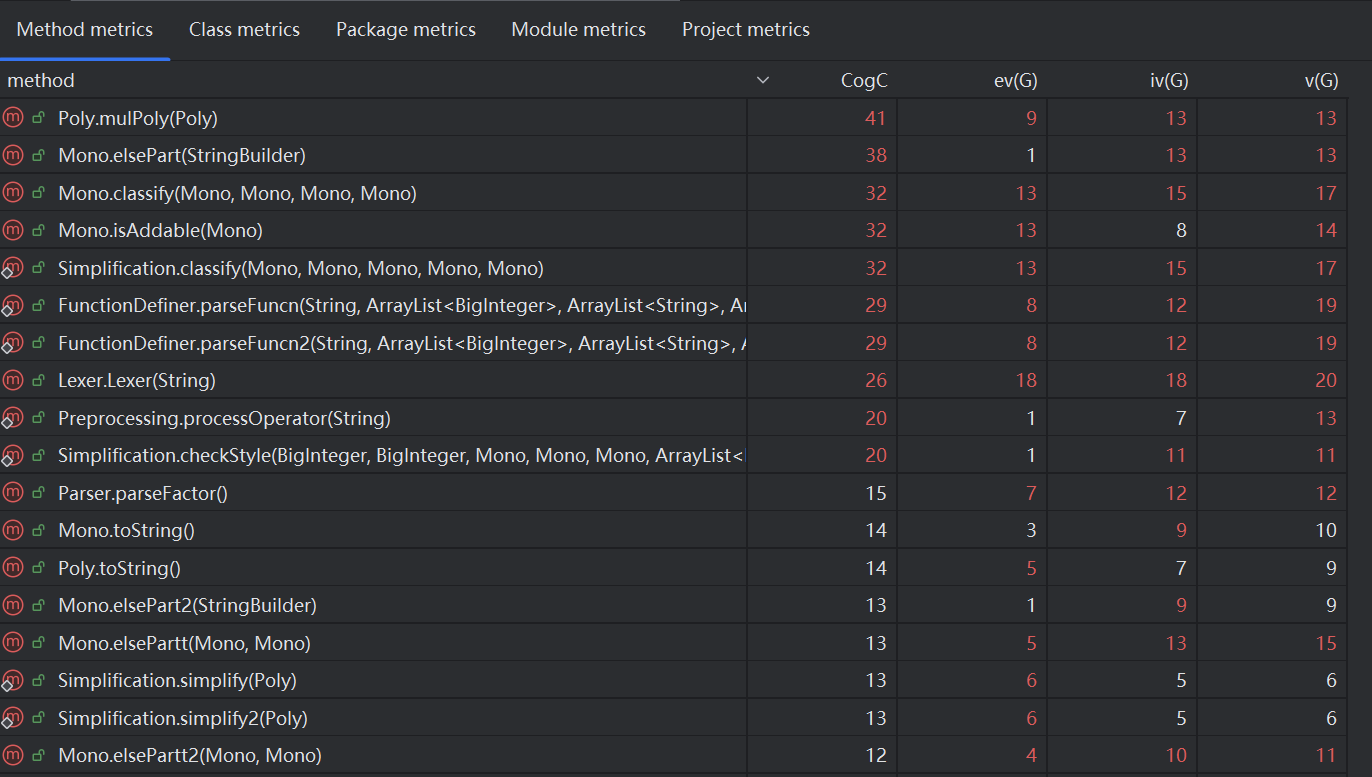
从图中能看出，我绝大部分方法的 Cognition Complexity（认知复杂度）是较低的，处于 0 ~ 15 的范围内，这代表这些方法复杂度较低，容易读懂。但是也存在少部分代码的复杂度极高，处于 20 ~ 40 的区间内，这部分方法很难让人读懂，说明在书写时考虑不周，采用了一些不好的框架思路，这是我需要反思和摒弃的。例如 Poly.mulPoly() 方法的复杂度高达41 ，我在书写这部分代码的时候将大部分内容都堆砌到了一起，而不是功能拆分和独立，这使得很多复杂方法聚合成一个方法，复杂度过高。经过反思后，我认为应当把一部分核心代码分离出去，从而降低方法整体的复杂度，这样有利于之后的维护和阅读。

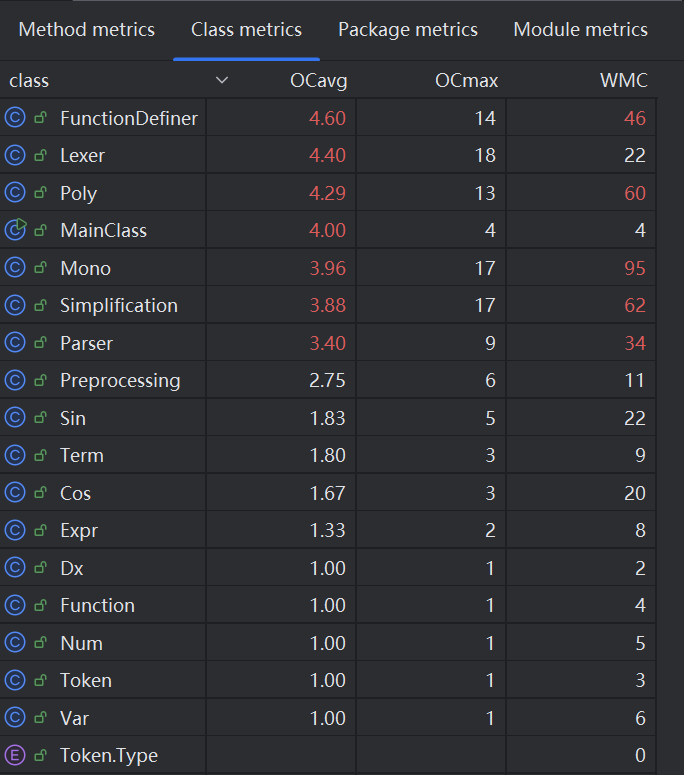
上图展示了我的类复杂度，可以看出两极分化较为严重，一半的类的平均操作复杂度和类方法加权数处于较低水平，说明这些类易于更改操作，方法复杂度较低。但是另一半的类的平均操作复杂度和类加权方法数严重过高，这部分类集成了大部分的核心复杂方法，致使更改困难，不易维护。我认为这种情况情有可原，毕竟这些类的作用本来就很强大和重要，他们就是要包含大部分的核心代码。例如 Simplification 类负责化简，这个类必然承担了所有的化简任务，而化简任务通常是复杂而繁重的，因此方法复杂度本身就很高，这部分代价很难降低。我们要做的不是强行降低算法的难度，毕竟有些算法就是很难；我们要做的是尽可能减少用到高难度算法，尽量用简单朴素的方式完成任务，这样可以规避高难度算法带来的高复杂度和潜在的难维护性。

2. 架构设计体验

本部分将会结合三次作业迭代的过程阐述我的架构如何逐步成型。

2.1 第一次作业

在第一次作业中，我就已经决定了程序的总体结构，并按照结构去填补框架与代码实现。我将程序结构分为两部分：解析和计算。前者是指将输入的字符串按照 Expr---Term---Factor 层次解析出来，并最终返回一个 Expr 类对象，存储整个输入表达式的信息。这部分操作主要是将原来平整的输入解析成有层次的组成部分，方便后续计算利用。后者是利用刚刚解析出的层次去计算表达式的展开，其核心是把 Expr、Term、Factor都转成由Mono组成的Poly，并利用Poly去计算。这部分操作是为了将表达式展开合并成最终的最简版本。这两部分彼此分离，各司其职，互不干涉。而针对作业，只需要分别设计这两部分的实现即可。

对于表达式解析，我采用了递归下降的方式，通过语法递归解析表达式并存储，形成层次化结构。其核心代码是：

 public Expr parseExpr() {
    Expr expr = new Expr();
    expr.addTerm(parseTerm());
    while (!lexer.isEnd() && (lexer.getCurToken().getType() == Token.Type.ADD
        || lexer.getCurToken().getType() == Token.Type.SUB)) {
        lexer.nextToken();
        expr.addTerm(parseTerm());
    }
    return expr;
}

 public Term parseTerm() {
    Term term = new Term();
    term.addFactor(parseFactor());
    while (!lexer.isEnd() && lexer.getCurToken().getType() == Token.Type.MUL) {
        lexer.nextToken();
        term.addFactor(parseFactor());
    }
    return term;
}

对于ParseFactor() 方法，需要先判断当前 Factor 的类型，例如是有符号整数还是幂函数，然后再去调用对应的 Parse 方法，返回一个Factor对象。

对于表达式计算，我采用了自底向上的方法。首先底层的 Factor 都要实现 toPoly() 方法，并且 Poly 类要具备：多项式乘法、多项式加法、多项式乘方这三种计算方法；对于 Term，需要对其中的每个 Factor 调用 toPoly() 方法并进行多项式相乘，从而将 Term 转成 Poly；对于 Expr，需要对其中的每个 Term 调用 toPoly() 方法并进行多项式加法，从而将 Expr 转成 Poly。这样就完成了表达式的计算。最后只需要将 Poly 输出即可。

在第一次作业中，我针对有符号整数和幂函数，设计了对应的 ParseNum() 方法和 ParseVar() 方法，并实现了各自的 toPoly() 方法。此时的Mono由系数和幂函数组成，形如：a*x^b。

2.2 第二次作业

在第二次作业中，新增了三角函数因子和自定义函数因子。整体程序架构延续了第一次作业的结构，还是两部分，因此只需要单独考虑新增部分如何实现同样的方法即可。

对于三角函数，需要新开一个类，并应用 Factor 接口，实现 ParseSin() 和 ParseCos() 方法，以及 toPoly() 方法。但是由于新增了三角函数，所以单项式Mono的组成发生了变化，变成了由系数、幂函数、正弦函数、余弦函数组成的单元，形如：ax^bsin(f1)^c…cos(f2)^d*…。这就需要重新设计多项式乘法、加法。考虑到合并的问题，我们还要设计多项式比较方法，而这依靠单项式比较方法。单项式比较方法里会比较三角函数是否相等，而这又要用到多项式比较方法，因此这是一个递归比较的过程。需要注意的是在进行操作的时候要注意深浅拷贝的问题，有时候我们需要根据现有的单项式返回一个全新的单项式，而不是直接在现有的单项式上做修改，因为这可能会影响之后的计算。

对于自定义递推函数，我新开了两个类，分别是Function类和FunctionDefiner类。前者用来作为自定义递推函数因子存储Expr，实现Factor接口，具备toPoly方法；后者用来做输入处理，预处理函数原表达式，并具有实参替换方法。具体流程为：在读入阶段，先读入f{0}，f{1}，f{n}的表达式，并去除空白符和连续符号。之后调用FunctionDefiner.addFunc() 方法并传入处理后的字符串。先找到f{0}和f{1}的表达式，直接作为原始表达式进行存储，并解析出参数列表存储。之后通过f{n}的递推式和已经算出的原始表达式进行实参替换，分别算出f{2}、f{3}、f{4}、f{5}的原始表达式。在解析自定义递推函数因子时，读入 f 的层数和实参，然后在原始字符串中进行实参替换，最后解析替换后的表达式并返回 Expr 对象，在toPoly的时候直接调用 expr.toPoly() 并返回即可。

通过以上处理，可以实现新增的三角函数因子和自定义递推函数因子的解析方法，满足了第一结构；同时实现了两个因子的toPoly方法，满足了第二结构。并根据变化改进了Poly的乘法、加法运算方式。这样就可以延续第一次作业的程序架构。

2.3 第三次作业

在第三次作业中，新增了求导因子和自定义普通函数。照样可以类比第二次作业的处理方式，延用一开始的作业架构，只针对性的新增底层接口，不改变整体核心代码。

对于求导因子，需要先对要求导的表达式进行解析，得到一个Expr对象。这时有两种选择：对 Expr --- Term --- Factor 层次求导，或者对 Poly --- Mono 层次求导。我选择了后者，因为我在对Expr进行toPoly的时候会有一些化简操作，这会简化Poly的复杂度，使得求导相对来说更简单。对Poly求导的方式是，对每个Mono求导返回Poly对象，之后进行多项式加法，因此需要实现Mono的求导方法。对Mono求导需要用到求导法则，分别对单项式中每一个单元求导乘上其他单元并相加。所以需要对常数因子、幂函数因子、三角函数因子实现求导方法；对单元求导需要应用链式法则，递归求导。需要注意求导过程中要对单项式进行深拷贝，这样不会影响原来的Mono。

对于自定义普通函数，可以沿用Function和FunctionDefiner类，只需要对预处理方法稍作变化即可。要注意自定义递推函数是有层次之分的，例如f{1}和f{4}，但是自定义普通函数没有，只能是g(x)或h(x)，因此可以把他们的层级默认设为0，方便沿用之前的架构。

通过以上方式就可以实现新增因子的解析方法和toPoly方法，这样就可以实现底层接口，沿用核心逻辑框架。

2.4 新迭代场景分析

为了检测该模型的可扩展性和可迭代性，现自行构造一个新的场景，并分析该架构如何扩展。

假设新增一个自然指数函数因子，形如 e^exp，其中e是自然对数的底数，exp是e的指数，是一个表达式。那么对于我的架构，只需要单独为其设计parseExp()解析方法和toPoly()方法，同时更改Mono的最小单元结构，并重写多项式加法、乘法算法，重写多项式比较方法、新增自然指数函数因子的求导算法。

对于parseExp()方法，需要新增一个Exp类，里面有一个Expr类型的成员变量，用来表示指数。在进行 parse 的时候，若没有^符号，则指数默认为1，否则为^后面的部分，可以通过传入一个字符串，在Exp构造方法内部解析的方式解析指数成员变量。这样就完成了parseExp()方法。

对于toPoly()方法，首先要扩展Mono的最小单元，加上自然指数函数，形如：ax^bsin(f1)^c…cos(f2)^d…e^(exp)。然后把exp进行toPoly操作，并存入Exp对象中，之后构造一个系数为1、x次幂为0，sin和cos均不含有，e的exp为自己的poly的单项式，并把这个单项式装入Poly中即可。

对于多项式比较是否相等，需要两两比较单项式是否相等，这需要在原来的基础上比较exp是否相等。多项式加法需要在除去系数以外相等的条件下系数相加，多项式乘法需要把exp相加。求导需要应用链式法则。

经过以上调整后，可以继续适配程序的架构。因此可见，该架构的可迭代性还是相对较高的。

3. 分析自己程序的bug

‘1. 在正确性上：由于我每次新增一个功能，或者经过一次迭代，就会对我的方法和程序进行相当充分全面的测试，因此在公测和互测阶段没有因为正确性而产生的错误。在自己检查的时候曾经出现过因为深浅克隆产生的bug：在多项式乘法的时候，我没有单独克隆出一个单项式用来表示将两个单项式相乘的结果，而是直接对其中一个单项式进行更改，这就导致该单项式在后续跟其他单项式乘法时已经发生了改变，最终导致错误。解决的方法就是克隆出一个等值的单项式并对其进行更改即可。

’2. 在TLE上：我在第三次作业时，在互测环节被刀了两次TLE，其本质是构造一个形如 sin(sin(sin(sin(sin(sin(sin(sin(sin(sin(sin(sin(x))))))))))))的表达式来让我的程序CPUtle超时。为什么会在处理这种样例时超时，本质上是因为我在sin中做了优化，在toPoly时会先检查sin括号内部是不是0，如果是0就直接返回0；同理在输出时我也会这样检查从而不输出含sin(0)的单项式。这种方式在遇到这种极端样例的时候会递归执行超过一亿次！解决方式就是关掉这个优化）不过我并不认为这是个bug，因为这样的优化在正常情况下是很有效果的，因此大家不用因此而担心，真的因此被刀只需要关闭优化即可修复。

4. 分析自己发现别人程序bug所采用的策略

我发现别人程序的bug主要通过两种方式：1. 评测机测试 2. 手搓边界数据

‘1. 关于评测机测试：我认为很有必要搭建一个评测机，既可以帮助自己和他人找bug，也可以在互测时候刀人。评测机搭建方法可以自行学习，之后只需要根据不同题目要求写数据生成器即可。此外还需要一个主程序来实现运行数据生成器、生成输出、比较输出、保存错误数据等功能，这个主程序一旦写好可以被反复利用。

’2. 关于手搓边界数据：自己在测试自己程序的时候，就可以积攒一些根据输入边界条件精心设计的数据，这些数据可以是极端样例、边界情况、复杂输入、化简样例等。这样既可以测试自己程序的正确性，还可以在找别人bug的时候检测这些易错点。

5. 分析自己进行的优化

我的优化主要集中在三角函数化简的部分。其主要内容如下：
sin(x)^2 + cos(x)^2 = 1
sin(x)^0 = 1
sin(0) = 0
cos(0) = 1
2sin(x)cos(x) = sin((2x))
cos(x)^2 - sin(x)^2 = cos((2x))
sin(a)*cos(b) + cos(a)*sin(b) = sin((a+b))
sin(a)*cos(b) - cos(a)*sin(b) = sin((a-b))
-sin((-x)) = +sin(x)
cos((-x)) = cos(x)

这些优化是通过单独的Simplification类实现的。Simplification类里面有检测两个单项式是否能进行化简的方法，也有进行化简的方法。具体方式是：先提取公共项，之后分析两个单项式不同的项是否满足特定的化简要求。真正化简的时候，传入一个ArrayList，通过下标索引找到要化简的两个单项式，并生成化简后的新单项式，然后在ArrayList中删除原来的两个单项式并添加化简后的单项式。
我的化简可以保证代码的简洁性和正确性，因为每一步都经过充分的检验和测试。

6. 心得体会

我认为这一单元的学习对我的程序设计能力有很大的提升。首先是程序架构的设计思想，我学会了分离的结构，把程序分成底层接口和核心代码，彼此功能分离，方便扩展和化简。其次是递归下降的处理思路，能够解决结构明确、细节复杂的很多问题，在今后的设计中也应当使用递归的思路去解决难题。最后是对Java代码能力的提升和评测机搭建能力的培养，我的代码能力得到了加强和巩固，也学会了评测机的书写思路。
总体上讲这三周并不算轻松，从周一到周日基本都没有停歇过，像不断运转永不停歇的车轮一样。也曾因为题目难度跨度大而迷茫困惑，但最终都在充分地思考后完美完成任务。
总之我认为第一单元的学习体验和收获都是很好的！