2025_BUAA_OO_Unit1总结

卢一非-23371282 2025-03-21 00:52:19

第一次作业
UML类图
架构分析
代码复杂度分析
第二次作业
UML类图
架构分析
代码量与复杂度分析
第三次作业
UML类图
架构分析
代码量与复杂度分析
优化方法
首项符号处理
合并同类项
三角函数的优化
可扩展性分析
BUG与HACK
我的代码所存在的bug
hack别人所用的策略
心得体会
未来方向

第一次作业

UML类图

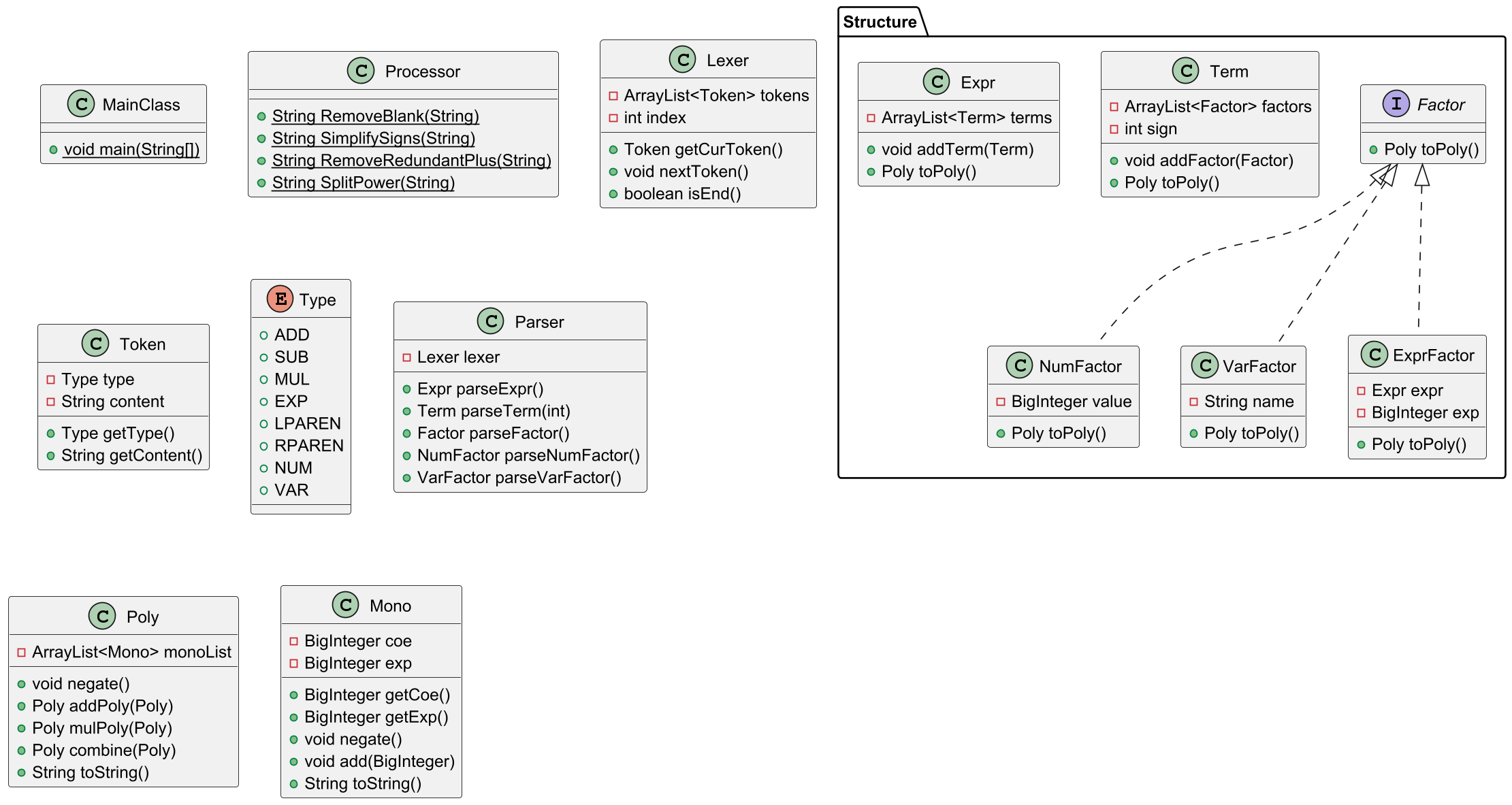
类图中左半部分的是功能类，具体功能分析见下“架构分析”；右半部分的是结构类。

架构分析

第一次作业进行的是最简单的加减乘及乘方任务。具体分析如下：

1.Processor 类：对表达式进行预处理，即去除空白项、处理连续正负号、处理冗余正号、将幂方拆成乘式（这一处理在第二次作业中有所更改）。
2.Lexer 类：对表达式进行词法分析，将符号的类型和内容以 Token 类形式存储。
3.Parser 类：对表达式进行递归解析，从顶层到底层依次存储为 Expr ， Term ， Factor 类，其中 Factor 类又分为 NumFactor ， VarFactor ， ExprFactor 类。
4.Poly 和 Mono 类：对 Expr ， Term ， Factor 类从底层向顶层使用自身的 toPoly 方法，统一存储为单项式和多项式形式。之后对 Poly 进行优化（合并同类项）和 toString 方法，得到输出结果。

代码复杂度分析

Method metrics

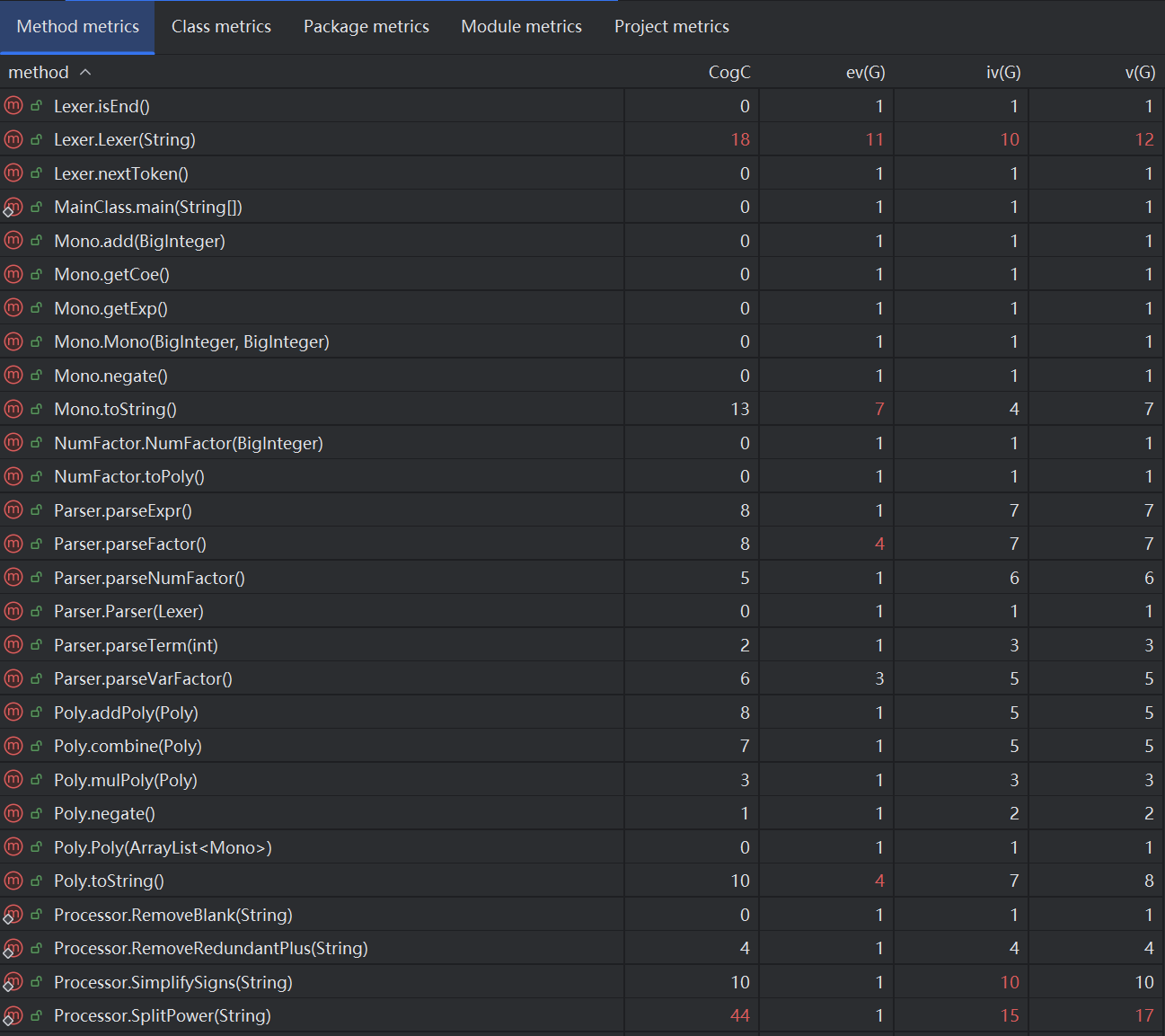
共6个方法复杂度超标。其中最复杂的两个为：

1.Lexer.Lexer(String)：直接采用了OOPre最后一次作业代码，由于字符类型很多，因此方法判断结构长。在第二次作业中，我将 pos++ 统一提出，减少了每个判断结构中的执行代码长度。
2.Processor.SplitPower(String)：利用字符串操作把幂方拆成乘式，这一操作是由于题目看漏，其实并无必要。在第二次作业中，我用 Poly 的 power 方法代替了这个方法。

Class metrics

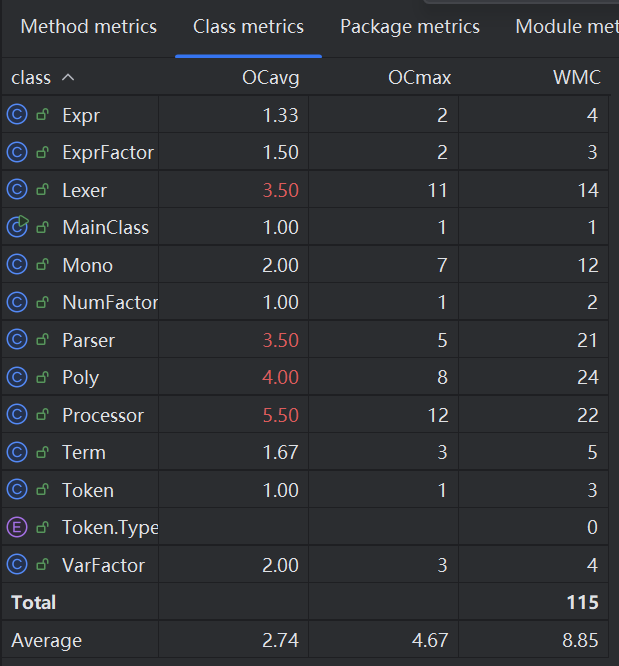
由于解析和展开的处理也很多，造成 Parser 和 Poly 类超标。

第二次作业

UML类图

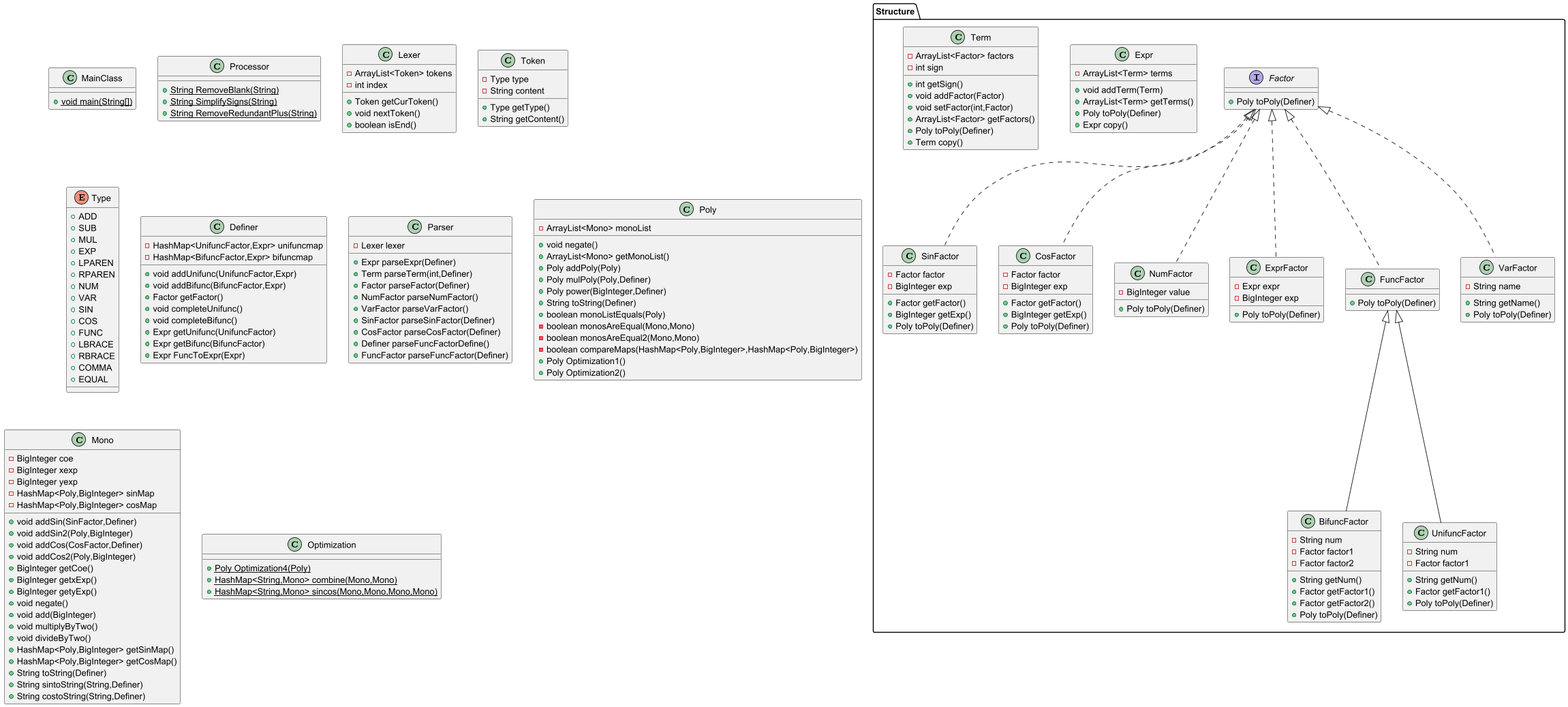
类图中， FuncFactor 下继承了两个类，但这里将 FuncFactor 设计为类而不是接口，导致后续迭代中出现了问题，对于方法的重写实现不合适。为了理清类与接口的区别，我查阅资料后发现，接口可以对行为进行定义，而将具体的实现留给实现类，这样一来，实现类和接口之间的耦合度就会降低，代码的可维护性和可扩展性得以提高。

架构分析

第二次作业新增了三角函数和自定义递推函数。具体分析如下：

1.三角函数的处理：新增了 SinFactor 和 CosFactor 类。在解析时，每个三角函数因子存入自身的括号内因子 factor 及指数 exp ；在 toPoly 时， Mono 类新增了 HashMap<Poly, BigInteger> 类型的 sinMap 和 cosMap，来存储单项式中不同三角函数的因子（已转为 Poly ）和指数。需要注意的是， toPoly 时若 Mono 中已有相同因子的同类三角函数，只需指数相加而不新增一个元素。
2.自定义递推函数的处理：新增了 Definer 类和因子 FuncFactor ， UnifuncFactor， BifuncFactor 类。在输入时，先将输入的定义表达式以 HashMap<FuncFactor, Expr> 形式存入 Definer 类中，再使用 complete 方法将 f(n) 表达式推广到 f(2) 至 f(5) （这里表达式仍含有前序函数）；在解析后，加入一步调用自定义函数，将函数全部转化为表达式因子（注意为避免括号丢失可能带来的错误没有转化为表达式），这一步具体通过 Definer 中的 get 方法实现，先将要调用的函数对应表达式中的函数因子（若有）用表达式因子代替（即递归调用），再利用字符串替换将形参换为实参。需要注意的是，在这一过程中，为处理形参 y ，我对 y 构建了同 x 一样的方法，这样代码适用性大大提升。还需要注意的是，双变量在字符串替换时可能因替换先后顺序而出错，因此先统一将形参换为 u 、 v 再换为实参。
3.幂方的处理：第一次作业中我利用字符串操作将幂方拆成乘式（起因是开始未注意到表达式因子也有指数），但在第二次作业可括号嵌套后不适用，因此改为了 Poly 中的 power方法。由此可见，图一时之快不能一劳永逸，在建构时需要考虑代码的可扩展性。

代码量与复杂度分析

Method metrics

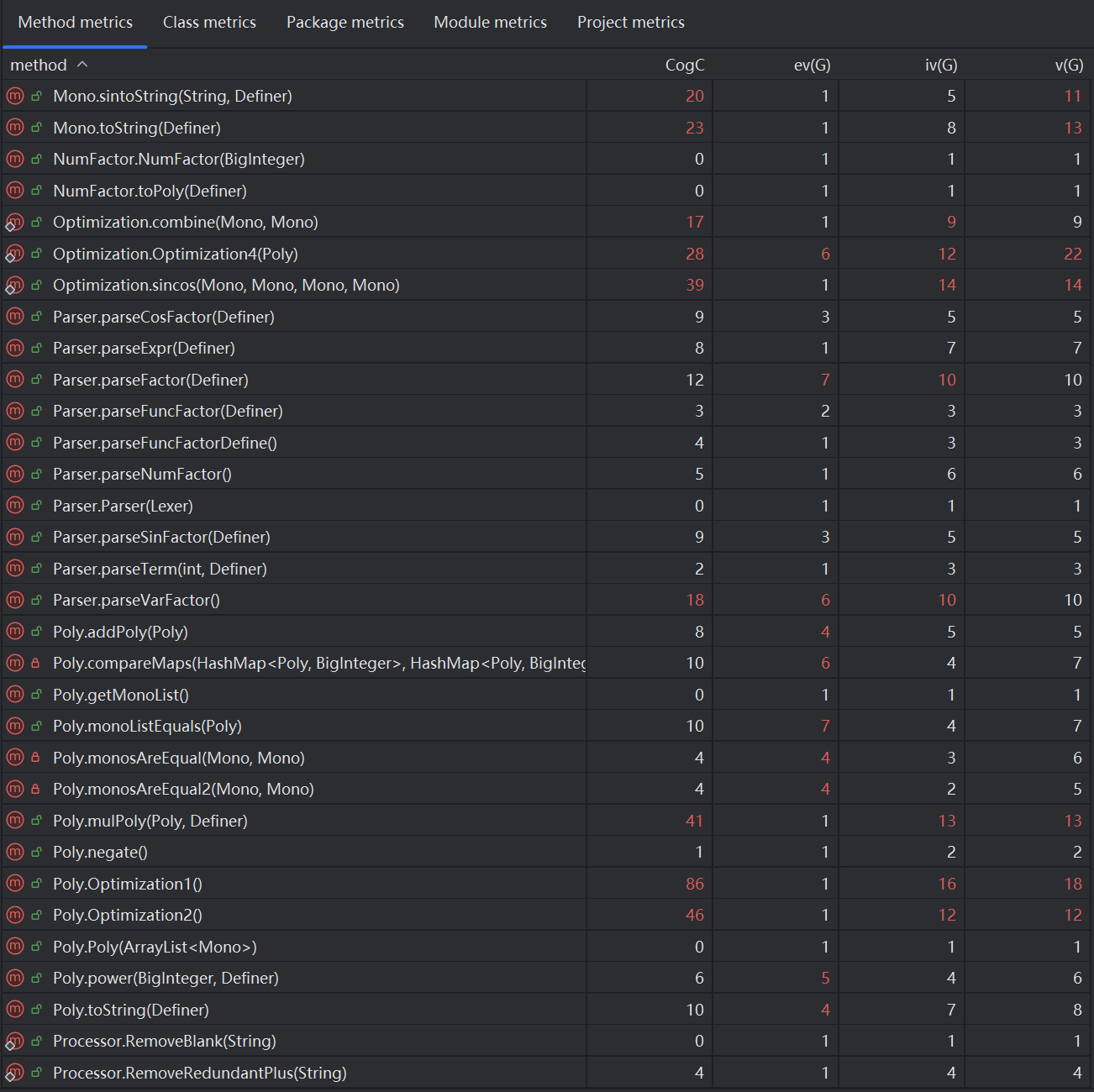
这次复杂度超标的方法明显增多...（

而重灾区应该在优化代码中，这归结于时间紧张思考不充分而导致代码过于复杂，也提醒自己今后动手前先思考清楚什么架构思路最简洁，理清思路再开始。

其他超标的还存在于递推函数解析等地方，由于我对递推函数展开了三次处理（f(n)推广、表达式中函数代入及形参代实参），导致从f(2)到f(5)进行多次重复累加处理，代码复杂度大大提升。

Class metrics

新增对递推函数的解析以及对三角函数的优化涉及方法较复杂，导致相应类复杂度超标。

第三次作业

UML类图

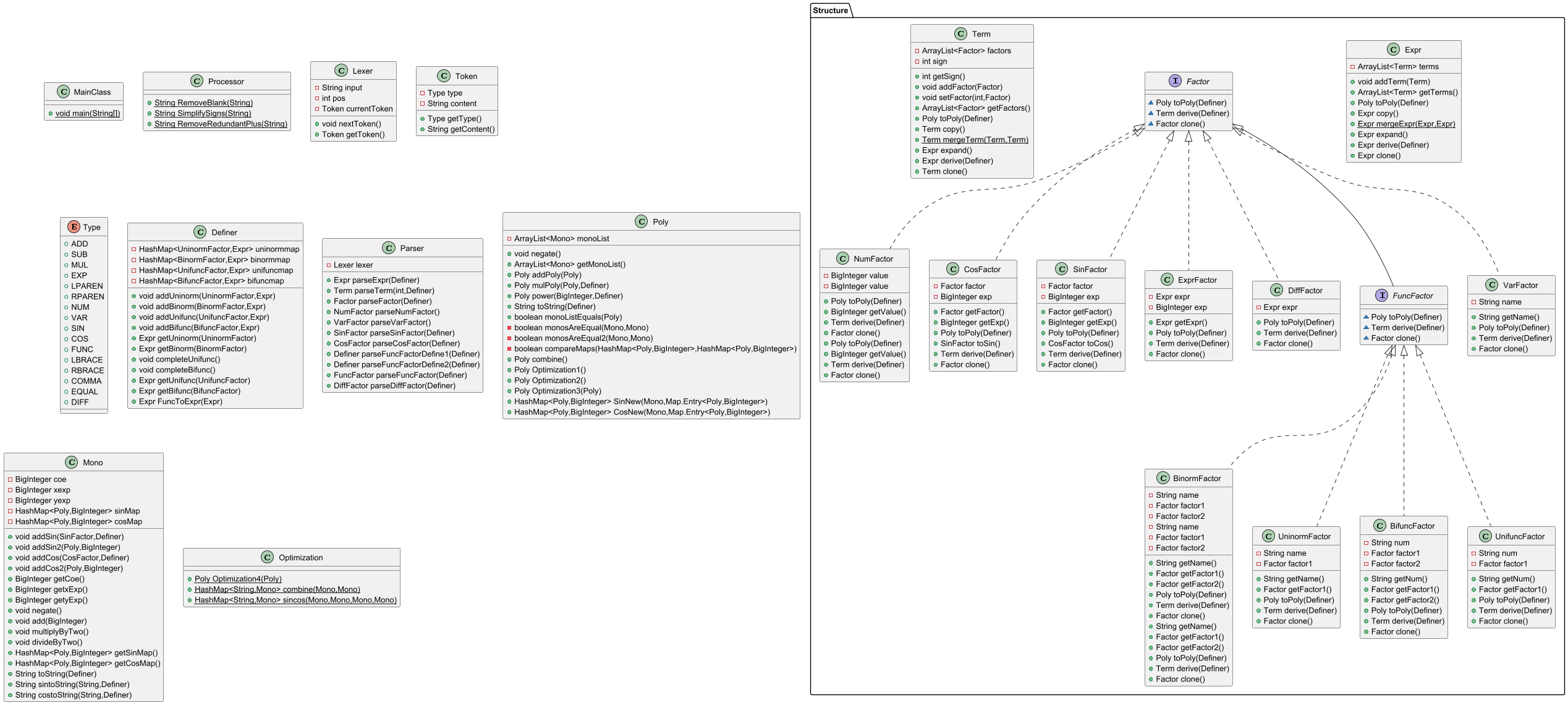
类图中， Factor 继承的子类较多，是因为我将不同类型的自定义函数、三角函数均分开构建类。这样的优点是分开处理结构更明晰，方法设计更有针对性，缺点是大大增加了类数和方法数。

架构分析

第三次作业新增了一系列自定义普通函数和求导算子。具体分析如下：

1.自定义普通函数的处理：基本同自定义递推函数，这里不赘述。
2.求导算子的处理：基本沿用第二次实验的代码。新增了 DiffFactor 类，对每个因子新增了 derive() 和 clone() 方法。

代码量与复杂度分析

复杂度超标情况和第二次作业基本一致，这里不多赘述。

优化方法

首项符号处理

我在输出时先遍历正项输出再遍历负项输出，这样有正项时可以去掉首项符号从而缩短输出长度。

合并同类项

对最终结果 Poly 使用 combine() 方法，遍历查找同类项并合并。

三角函数的优化

1.利用三角函数公式优化：这里我使用了四个公式优化，分别是
$$ \sin(x)^2+\cos(x)^2=1 $$

$$ 2\cdot\sin(x)\cdot\cos(x)=\sin(2x) $$

$$ \cos(x)^2-\sin(x)^2=\cos(2x) $$

$$ 1-\sin(x)^2=\cos(x)^2,1-\cos(x)^2=\sin(x)^2 $$

每个公式我建立了对应的一个方法来优化。由于第二次作业时间较为紧张，我的这四个方法格式不够统一，其中一个尝试了博客中的比较差异项方法，另外几个分别有自己的思路方法，这导致代码量很大且阅读难度较大，这一点可以继续简化改进，将方法通用部分提出来简化思路。不过大体思路都是利用内外迭代器叠加循环，循环中利用判断条件（如系数和为0、因子相同、指数为2等）找到符合的项，再根据公式对项进行增添变换。需要注意的是，使用多个迭代器同时循环（尤其是循环同一个对象）时，容易发生迭代器错误，在增删元素后需要重置迭代器并跳出再重新循环。

2.将三角函数内负号提出：我向 Mono 中加入三角函数时，先判断三角函数因子是否为单项且有负号，若是则把负号提出。需要注意的是，正弦函数提负号时，若指数为偶次方则 Mono 的系数不用变。

3.对特殊三角函数赋值：我直接将 sin(0) 存为 0 ， cos(0) 存为 1 。需要注意的是， sin(0) 指数为0时存为1。