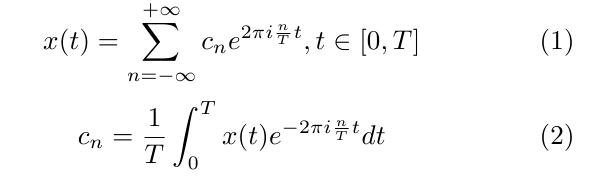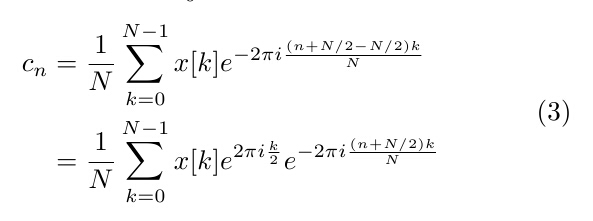CUFFT库实践（2）

[adagio_chen]

若要熟练掌握一个库的使用，特别是数学相关的库，去熟悉一下它的原理还是有必要的。如果仅仅看看自带的例子，照老虎画猫，恐怕只能知其然而不知其所以然，遇到新的问题时就不知道该怎么调整算法和参数了。

对于离散傅立叶变换的公式，有些书上讲到“其实它并没有物理意义，只是为了工程上的计算而已”。那么用FFT程序变换得到的数值代表什么意义？是频率么，是什么范围内的频率？

不妨来看一下傅立叶级数的的公式。设x(t)为一个定义在[0, T]上的一维信号，则：


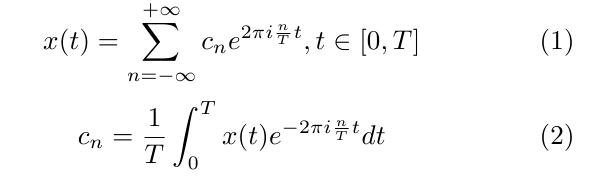
可以看到，当我们用黎曼求和方式吧公式（2）写成离散表达式，并且n=0,1,2,3....时，就是（为归一化的）离散傅立叶变换公式。实际上，很多时候我需要的频谱值是从[-N, N]采样的。这个时候，便需要对频谱做一下平移。即



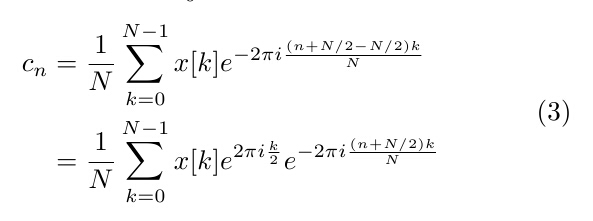
高维情况下也是类似的原理，这里给出一个三维的例子：

__global__
void TranslateSignal(int N, float3 d, float2 *signal)
{
	int i = threadIdx.x;
	int j = blockIdx.x;
	int k = blockIdx.y;
	int index = k * N *  N + j * N + i;
	float3 t = make_float3(i,j,k) / N;

	signal[index] = ComplexMul(signal[index], ExpPI(dot(t, d)));
}

[不可触碰]

虽然看不到懂，，帮顶，，，感觉把CPU程序改成GPU程序好难