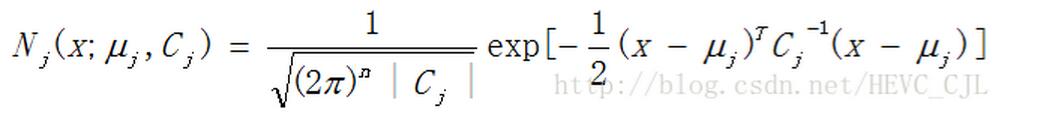高斯混合模型中的概率分布问题

[liuboning680680]

这段matlab程序之前已经在协方差矩阵的对角线加了一个很小的数，就是为了防止协方差矩阵的出现，得出来的结果却觉得也不对，混合高斯概率不应该是小于一的吗？我下面会贴出结果。

function gp=GaussianPDF(data,u,sigmai)
%UNTITLED3 此处显示有关此函数的摘要
%   此处显示详细说明
[m,n]=size(data); 
u=mean(data,1);
nxt_item(1:m)=0;  
tem_data=data-repmat(u,m,1);  
sigmai=sigma(data);
for i=1:m  
   pre_item=1/sqrt(((2*pi)^n)*abs(det(sigmai)+realmin));
   tem_data_t=tem_data(i,:)';  
   nxt_item(i)=exp(-0.5*(tem_data(i,:)*inv(sigmai)*tem_data_t)); 
end  
  
gp=pre_item*nxt_item;  
  
end  

下面是我的输入和结果

>> data=[1,2,3;4,5,6;7,8,9]

data =

     1     2     3
     4     5     6
     7     8     9
 u=mean(data,1)

u =

     4     5     6
>> sigmai=sigma(data)

sigmai =

    9.0000    9.0000    9.0000
    9.0000    9.0000    9.0000
    9.0000    9.0000    9.0000

>> GaussianPDF(data,u,sigmai)

ans =

   1.0e+03 *

    1.4823    2.4439    1.4823

我觉得这个结果不对，但又不知道如何继续

[liuboning680680]

我是楼主，是以这个公式为基础的

[liuboning680680]

已经在协方差矩阵对角线加上了很小的数，防止奇异矩阵的问题出现，但是这个结果也很奇怪，我还不知道问题出在哪儿

[我们最后一次收割彼此从此仇深似海]

opencv里的函数算出来也是有大于1的情况，楼主解决了吗

[leekwoksun]

本来就没错 概率密度不等于概率 公式给出的是概率密度的公式 是可以大于1的