434
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享最大子段和
给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时,定义子段和为0。
要求算法的时间复杂度为O(n)。
输入格式:
输入有两行:
第一行是n值(1<=n<=10000);
第二行是n个整数。
输出格式:
输出最大子段和。
输入样例:
在这里给出一组输入。例如:
6 -2 11 -4 13 -5 -2输出样例:
在这里给出相应的输出。例如:
20
其实,对于这于求最大字段和的问题,用动态规划的思想可能更好解决;毕竟这类问题一旦变形,动态规划只需要找出新的状态转移方程即可,而用分治法要调整、筛选的功能部分就麻烦些。当然,对于上面这个问题,用分治法解决也是绰绰有余。
首先是:分治法的思想就是将一个大问题分解为几个小问题求解,这里的大问题就是一整串字段的最大和,那我们可以将其看作几个小问题——
如果用leftSum,rigthSum,midSum表示上述三个子问题的解,那么maxnum = max( midSum, max( leftSum, rightSum ) );——(怎么还是动态规划的感觉//////)
因为本人伪代码写的不好,所以这里直接上代码:
#include<iostream>
#include<math.h>
using namespace std;
int MaxSum(int* arr,int left,int right);
int main()
{
int A[10010];
int n;
cin >> n;
for(int i = 0; i < n; i++) {
cin >> A[i];
}
int S = MaxSum(A,0,n-1);
// printf("最大字段和为:");
printf("%d\n",S);
}
int MaxSum(int* arr, int left, int right) {
if(left >= right) {//进来首先想着要出去
if(arr[left] < 0)//因为题目要求,全为负数则最大字段和应该为0
return 0;
else
return arr[left];
}
int leftSum = 0 , rightSum = 0, midSum = 0;//左子问题,右子问题,中间子问题的答案
int mid = (left + right) / 2;
leftSum = MaxSum(arr, left, mid);//求解左子问题
rightSum = MaxSum(arr, mid+1, right);//求解右子问题
int mid_leftSum = 0, mid_rightSum = 0;//求解中间子问题,定义向左向右延申的最大字段和
mid_leftSum += arr[mid];//初始化
mid_rightSum += arr[mid+1];
int temp = mid_leftSum;//用temp作为临时变量
for(int i = mid-1; i >= 0; i--){
temp += arr[i];//一直向左加
if(temp > mid_leftSum) {//一旦发现比原来更大的字段和,更新
mid_leftSum = temp;
}
}
temp = mid_rightSum;//再对右边进行同样的操作
for(int i = mid+2; i <= right; i++){
temp += arr[i];
if(temp > mid_rightSum) {
mid_rightSum = temp;
}
}
midSum = mid_leftSum + mid_rightSum;//将两边的延申的最大字段和相加
return max(midSum, max(leftSum, rightSum));//返回三个字段和最大的值就是原问题的解
}
用分治法将一个大问题分成了两个规模为自身一半的子问题,同时求从中间向两边延申的问题解的时间复杂度应该为O(n)
所以算法的复杂度公式:T(n) = 2T(n/2) + O(n) = nlogn 。
分治法为四大算法思想之一,其本身的价值其实轮不到我们来评判,实践已经证明。
其实我们很早就已经接触过分治法的思想。包括在数据结构中,二叉树的遍历、查找就是典型的例子。
我觉得分治法最大的好处在于,对那些复杂的问题,却可以不断划分为那些问题,将5451561161 + 165115446 的问题转化为1 + 1 的问题,写起代码来也十分的清晰,方便好用。但是限制就由于是分治法有划分、求解和归并三个过程,一题多解的情况下,比起其它更优质的算法,时间复杂度可能会更大一点。
另外最近我参加IPCP网络赛就遇到一道问题,题目大意为:
Alice 和 Bob 都是聪明绝顶的孩子,他们相约在一起玩游戏:给出一串长度为n的数组,两个依次从数组中取一个数,但是要求只能从队首和队尾取,且必须比上个取的数要大,现在给出一段数组,谁不能再从数组中取出数字,谁就算输了。Alice 先手,在两人都选择最优解的情况,输出胜利者的名字。
…………(省略一段堆)
输入样例:
6 2 3 4 4 3 1输出样例:
Alice
这道题,我一开始没有头绪,找了很多规律都感觉不对。
最后突然想到了最近在学的分治方法,索性干脆暴力一把。(后面超时改了很多次,最后卡时间过了)
即把大问题看作分别从两边开始选的问题的解,因为Alice先手,那么只要有一个返回值为Alice赢时,Alice就必胜。但是进入第二个层子问题分治时,这个判断条件就相当于变成了Bob先手,所以可以多设定一个flag的值来判定当前的返回规则,思想大致入图:
分解:将对一大串数组的求解方法转化为,分别先选两边的数再看n-1问题规模的求解。
求解:只要有一方不能再取,就返回对方获胜的信息,需要设置一个flag来判断当前是谁的回合。
合并:因为有队首和队尾两种问题的解法,同时Alice先手,那么只要有一个返回值为Alice赢时,Alice就必定取胜;但进入第二层次的子问题时,就相当于变成了Bob先手,所以flag的值也在设置当前的返回条件。
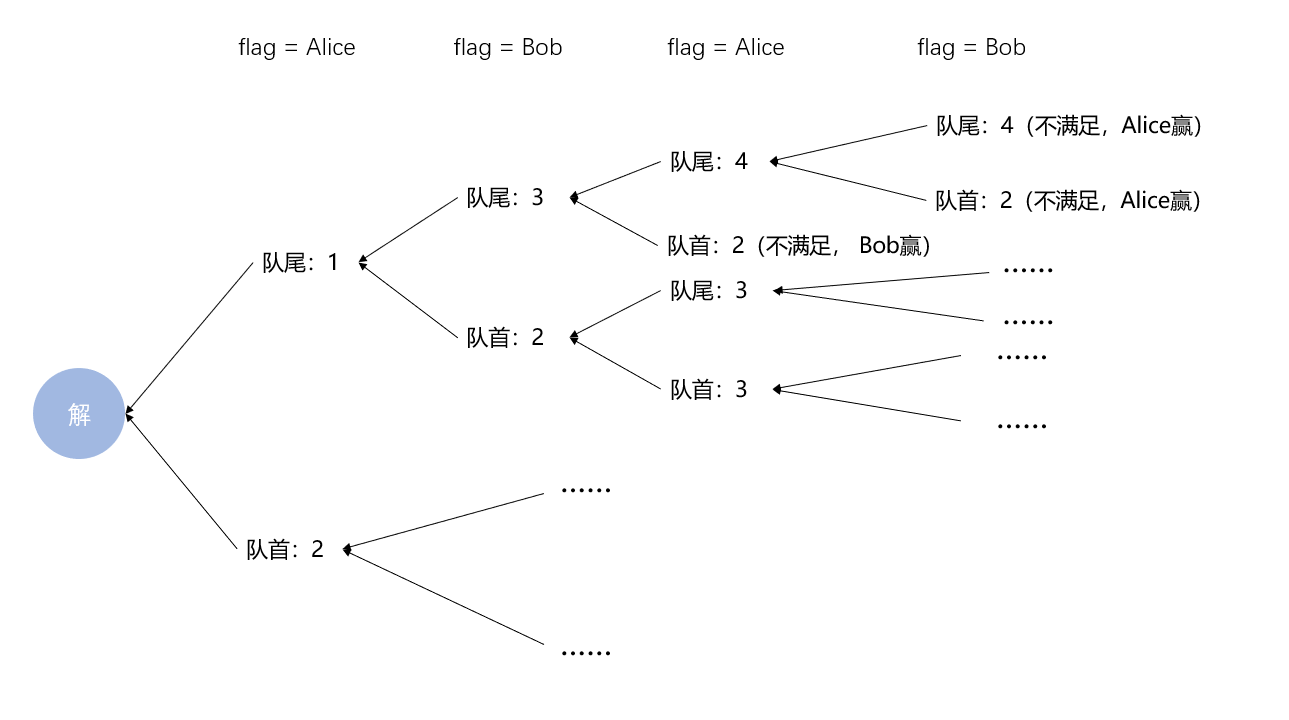
最后的Alice和Bob问题,获胜的条件是对方没有办法再从数组里面取数