算法设计与分析第五章作业

[计科2101袁正毅]

1.1 说明“最小重量机器设计问题"的解空间

解空间为解空间树的每个分支。测试用例n = 3，m = 3时，该问题的解空间为：

{(1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 2, 1), (1, 2 ,2), (1, 2, 3), (1, 3, 1), (1, 3, 2), (1, 3, 3),

(2, 1, 1), (2, 1, 2), (2, 1, 3), (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 3, 1), (2, 3, 2), (2, 3, 3),

(3, 1, 1), (3, 1, 2), (3, 1, 3), (3, 2, 1), (3, 2, 2), (3, 2, 3), (3, 3, 1), (3, 3, 2), (3, 3, 3)}

1.2 说明 “最小重量机器设计问题"的解空间树

如图

 

 

 

 

 

 

 

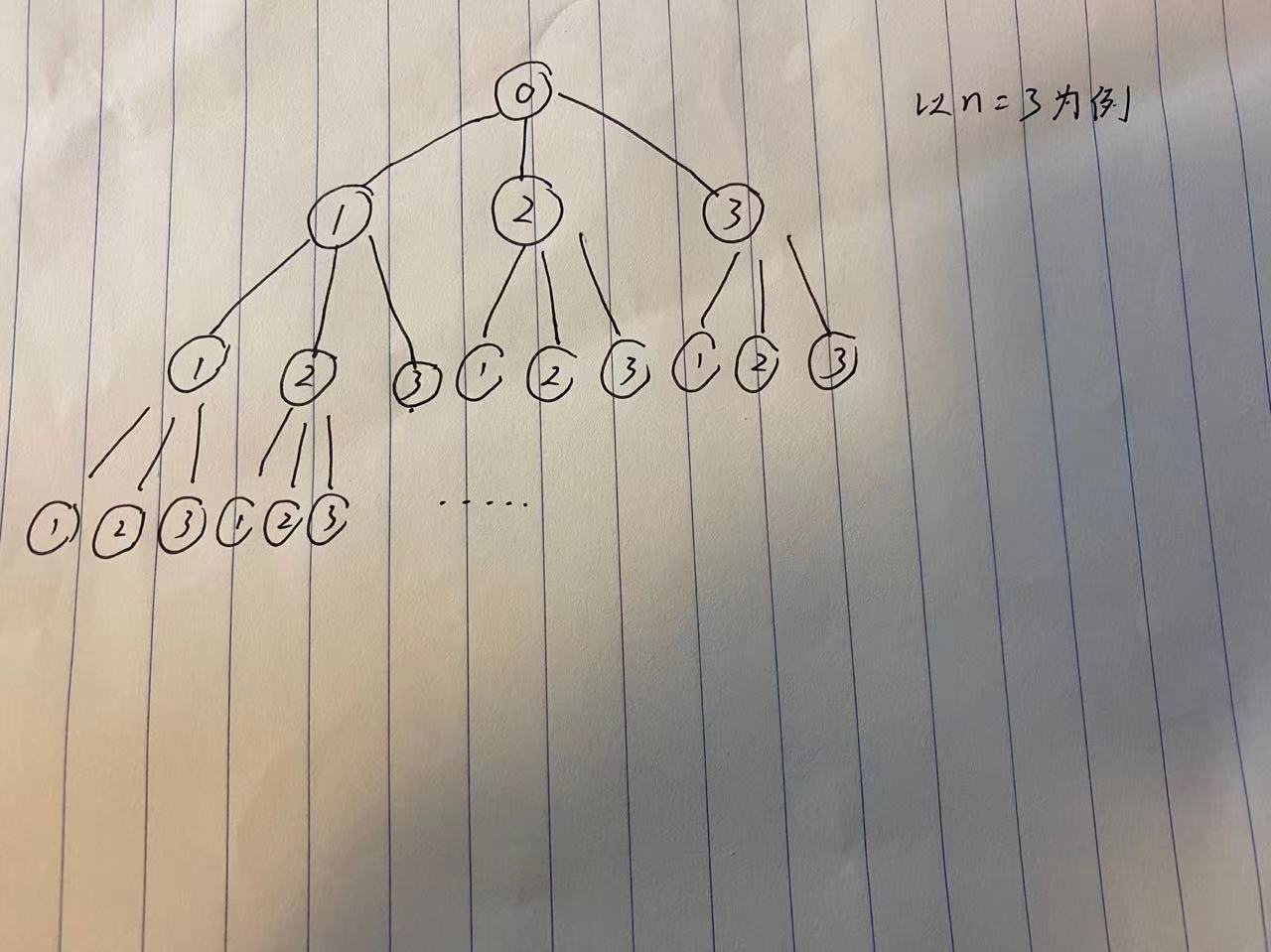
1.3在遍历解空间树的过程中，每个结点的状态值是什么

  当前已选部件的质量之和与价值之和

2. 你对回溯算法的理解

        回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树，当算法搜索至解空间树的某一节点时，先利用剪枝函数判断该节点是否可行（即能得到问题的解）。如果不可行，则跳过对该节点为根的子树的搜索，逐层向其祖先节点回溯；否则，进入该子树，继续按深度优先策略搜索。

        回溯法的基本行为是搜索，搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类：1. 使用约束函数，剪去不满足约束条件的路径；2.使用限界函数，剪去不能得到最优解的路径。问题的关键在于如何定义问题的解空间，转化成树（即解空间树）。解空间树分为两种：子集树和排列树。两种在算法结构和思路上大体相同。

[programmer_ada]

您可以前往 CSDN问答-数据结构与算法 发布问题, 以便更快地解决您的疑问