383
社区成员
面向对象第一单元总结
第一次作业
目标
通过对表达式结构进行建模，完成多变量多项式的括号展开，初步体会层次化设计的思想。
hw1基本思路
通过观察，发现表达式主要包含三部分——Expr，Term，Factor，而Factor 又由幂函数因子、常数因子、表达式因子构成。基于面向对象的知识，我对其分别建类。对于表达式的解析，我采用递归下降的处理方法，并在解析前用Process对输入的表达式进行预处理（如空白字符和连续的符号），使处理过的字符串不存在连续的符号，方便用Lexer分解出每个语法单元。
对于数据的存储结构，可以得到表达式的最终展开结果应该是一个多项式的形式:
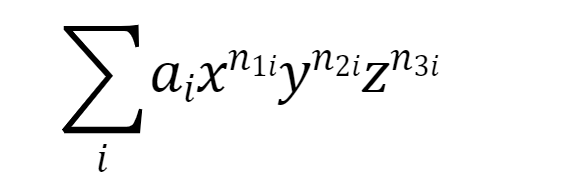
所以我建立了Poly(多项式类）和 Mono（单项式类)来存放数据，Mono类存放每一项的系数和x、y、z指数，Poly中建立ArrayList容器，来存放Mono,最后重写各个类中的toString 方法进行输出。
UML类图
使用plantuml进行绘制。(感觉摆放位置不是那么方便）
代码规模
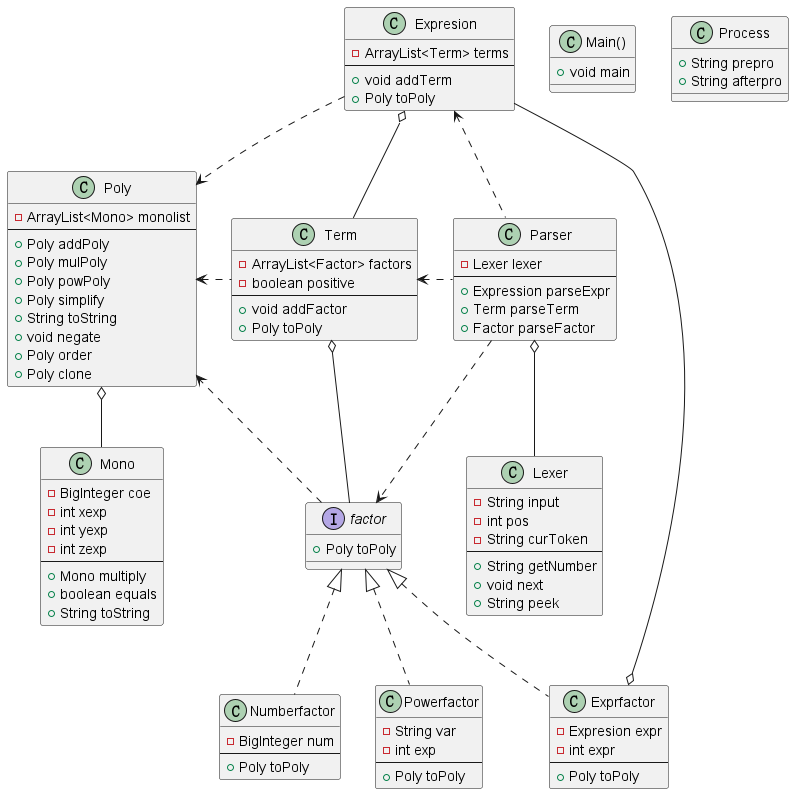
主要集中在Poly类中，其他类代码不算很多。
复杂度分析
方法复杂度
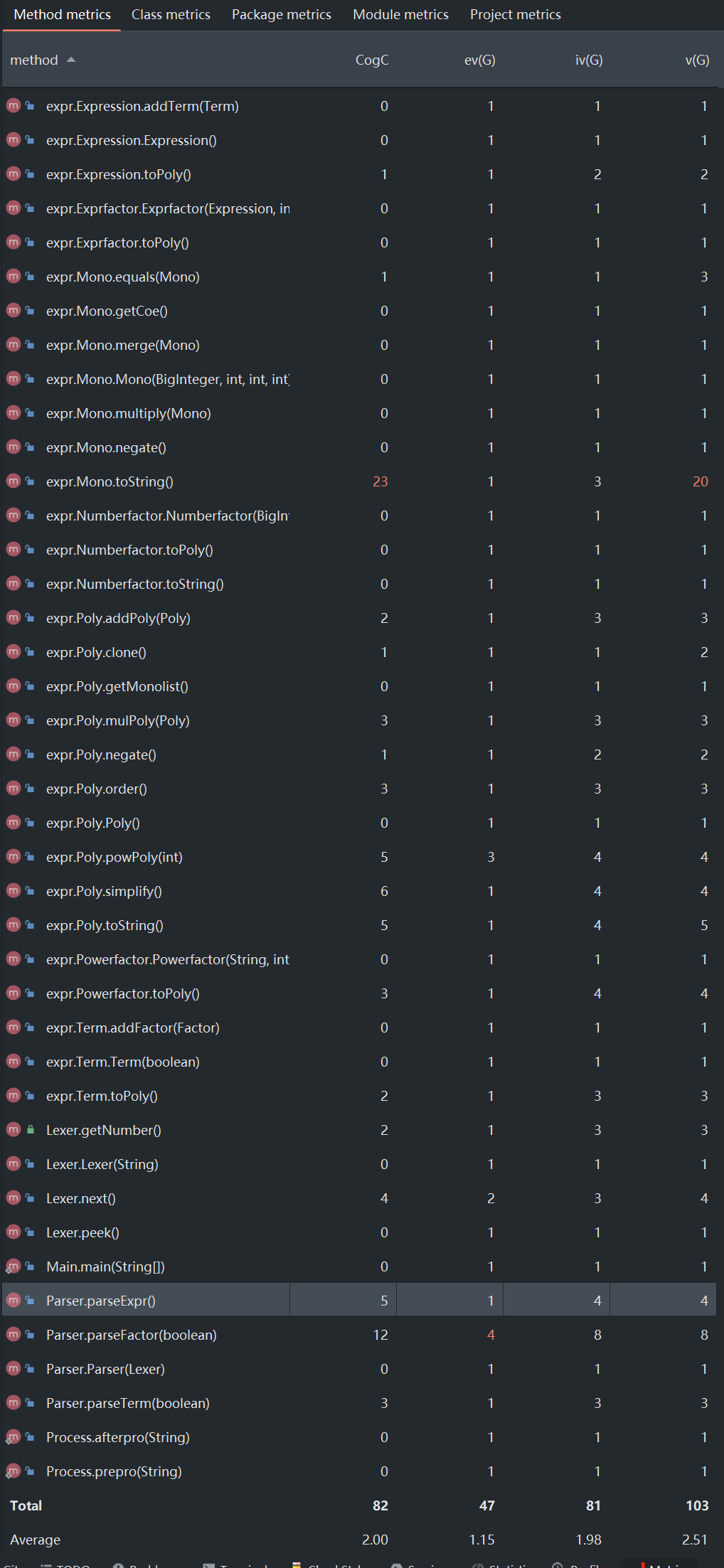
可以看到，整体的复杂度并不高。但可以发现Mono类中toString()方法的复杂度较高，在单项式转化为字符串时候，需要对所有情况进行分析讨论，并且我在这里作了进一步的优化，如x*2->xx，系数1的省去，所以需要较多的if else 语句，复杂度较高。
类复杂度
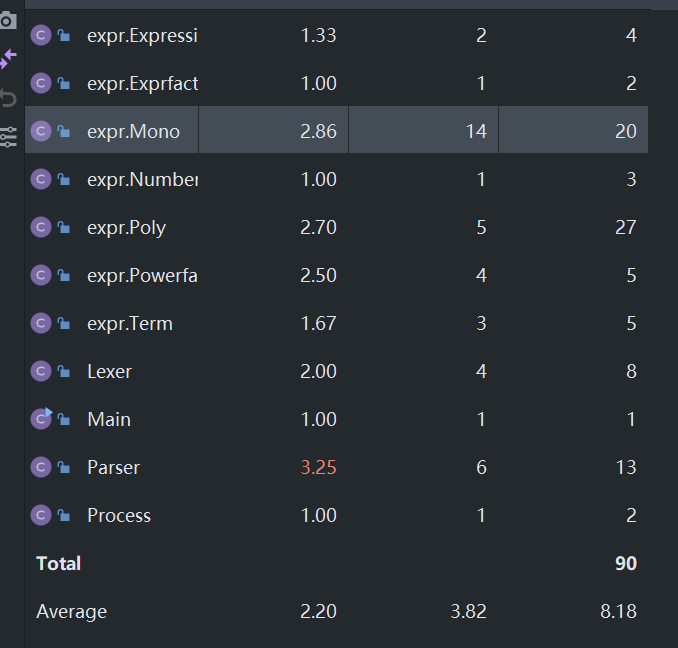
可以发现其中Parser类的方法复杂度较高，这是因为parser类作为递归下降的分析器，大量调用了Expr，Term，Factor的方法。
Bug分析
自己程序的Bug
第一次作业强测和互测均未出现bug。
他人程序的Bug
第一次作业时不会写评测机，抱着试试看的态度随便捏了几个数据，找到了他人代码的一个bug,输入--x**0会输出-1，推测是解析幂函数因子时候连续的负号没有处理好。
第二次作业
目标
通过对表达式结构进行建模，完成多项式的括号展开与函数调用、化简，进一步体会层次化设计的思想。
hw2基本思路
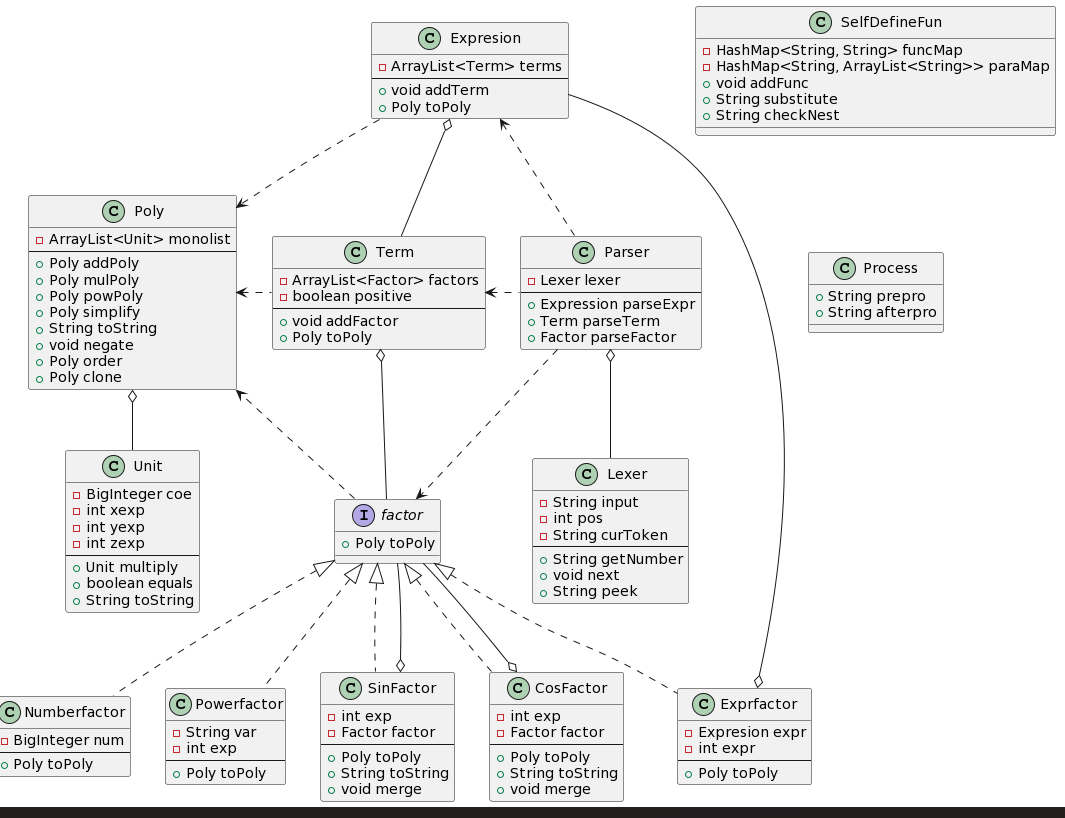
第二次作业在第一次作业的基础上新增三角函数因子，自定义函数因子，并支持括号多层嵌套，由于递归下降算法的优越性，在第一次作业中就已经可以处理多层嵌套的括号了。对于子定义函数因子，我新增了SelfDefineFuc类，并在递归下降解析前先对输入表达式中的函数因子进行形参、实参的字符串替换，对于三角函数因子，也是这次作业的重点，我新增了SinFactor和CosFactor类。
由于引进了三角因子，所以本次作业的多项式的最小单元变成了
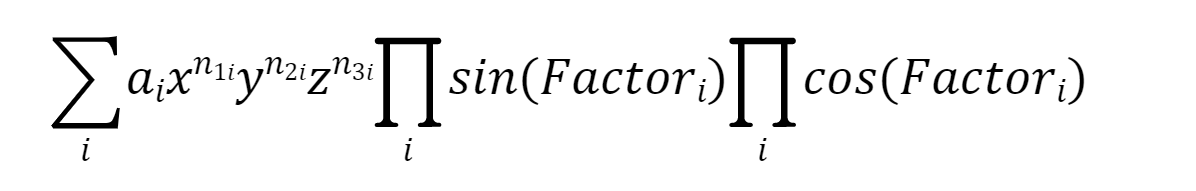
在Poly 中，addPoly()、mulPoly()、powPoly() 和最后的toString()方法需要一些小修改，不过，我觉得第二次作业最难的在于三角函数的优化及合并同类相的处理（如何判断相等），代码量也主要堆在这一块，这将在稍后分析。
UML类图
代码规模
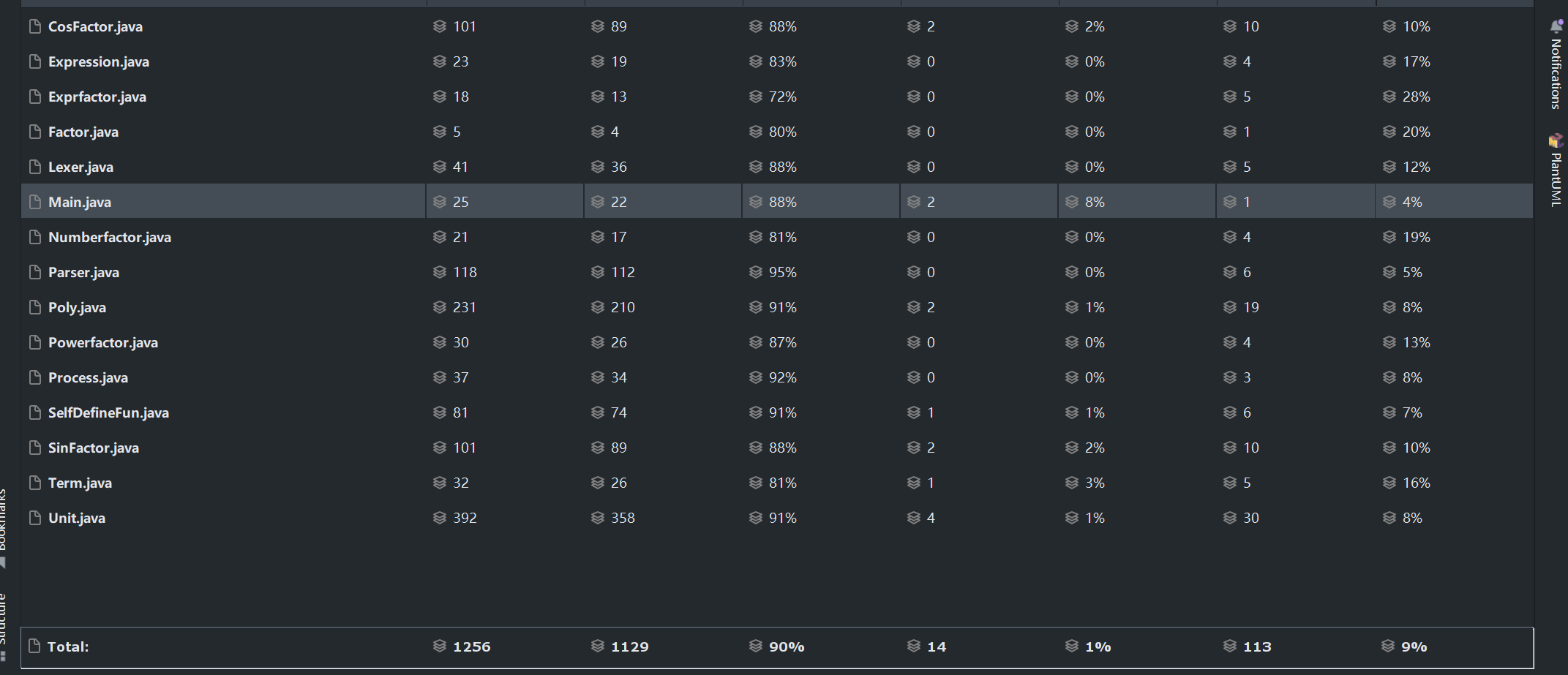
代码量比第一次还是多了不少的，不过感觉自己在优化方面写了比较多的重复的东西，比如equals的重写，对于三角函数的内部factor的equals判定，是需要系数也相等的，所以我又多加了个40行的equals1，相比于equals只是多了一行系数相同的判定，感觉代码冗余度较高。
复杂度分析
由于方法比较多，所以只显示Poly、Unit两个类中的方法（其他类中的方法的复杂度均较合理）
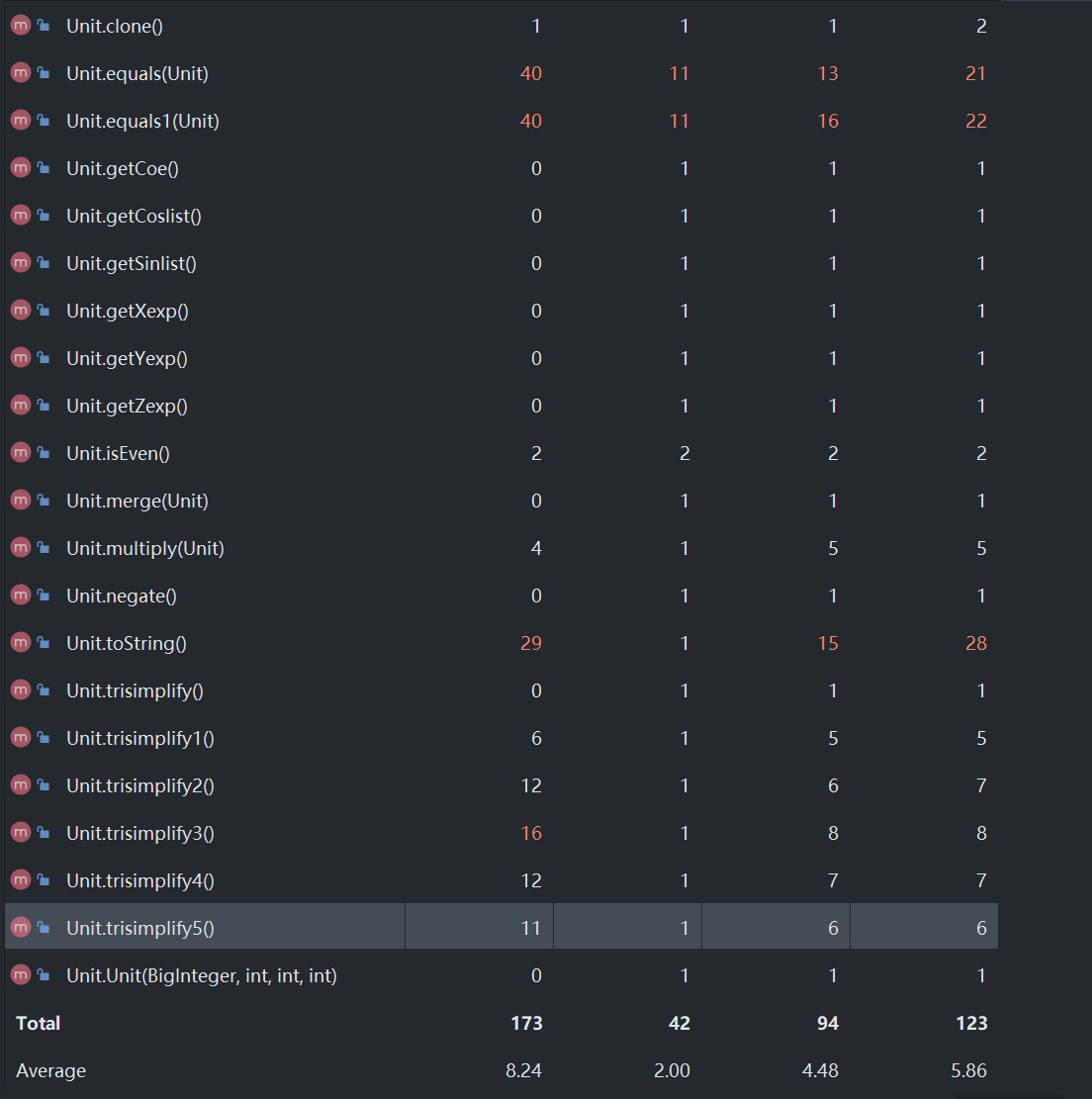
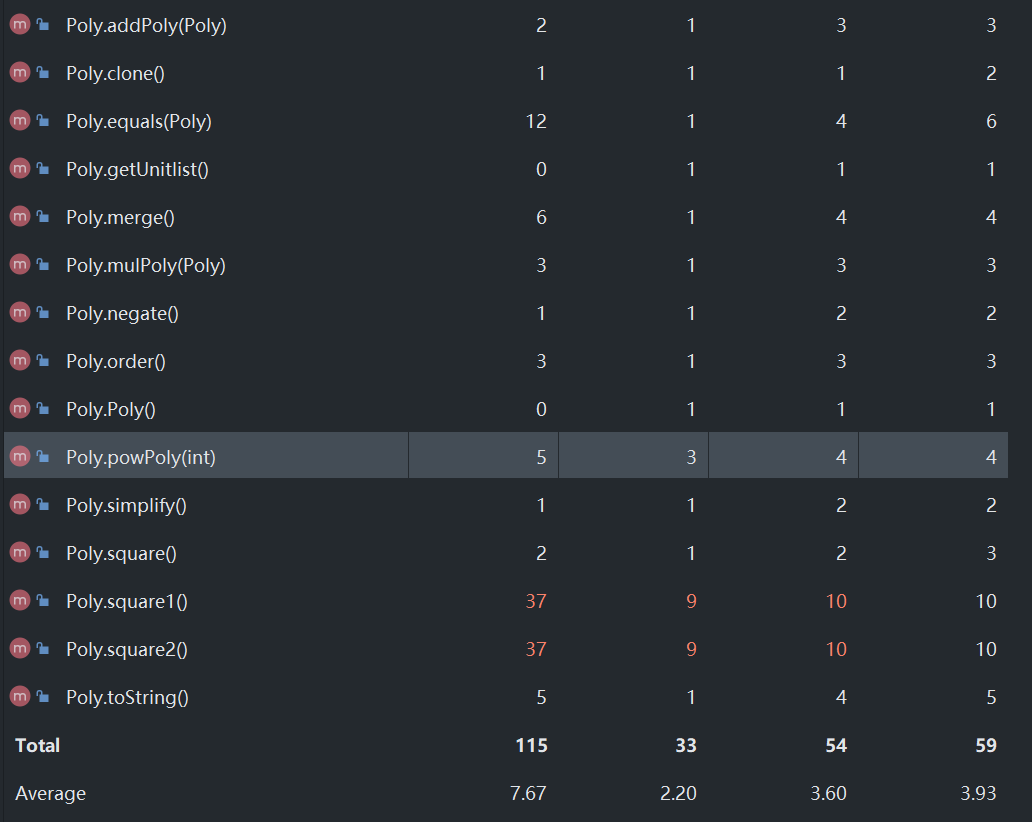
可以发现Poly和Unit两类中不少方法的复杂度较高，主要是加入了cos、sin两个因子，并且三角函数优化的逻辑写的有点复杂。
优化实现
在第二次作业中，我实现了二倍角、平方和、sin(0)=0、cos(0)=1、合并同类项、判断factor toString时是否需要加括号的优化。对于二倍角、平方和、合并同类项的优化有个共同的难点，如何判断内部factor是否相等，如sin((sin(x)+1))、sin((1+sin(x)))、sin((2-1+sin(x)))这些。我也是采用了递归的方法，将factor toPoly后进行比较，要比较两个Poly相等，就需要判断两个Unit相等，如果Unit中有三角因子项，再递归调用其facot.toPoly.equals(Poly other)，这样一层层判断下去，肯定不是无尽的，注意在比较两个Poly相等之前要对其进行化简，这里也就递归调用了自己，所以这些优化方法的复杂度都较高。
if (sinlist.get(i).getFactor().toPoly().simplify().equals(coslist.get(j).getFactor().toPoly().simplify())
对于判断是否是因子的优化，我也是采用factory.toPoly()的方法，如果其Unitlist只有一项，再判断是否是最基本的因子类型。
Unit unit = inner.getUnitlist().get(0);
int xcnt = 0;
int ycnt = 0;
int zcnt = 0;
int sincnt = 0;
int coscnt = 0;
if (unit.getXexp() > 0) { xcnt = 1; }
if (unit.getYexp() > 0) { ycnt = 1; }
if (unit.getZexp() > 0) { zcnt = 1; }
if (unit.getSinlist().size() > 0) { sincnt = 1; }
if (unit.getCoslist().size() > 0) { coscnt = 1; }
int cnt = xcnt + ycnt + zcnt + sincnt + coscnt;
if ((unit.getCoe().compareTo(new BigInteger("1")) != 0 && cnt > 0) || cnt > 1) {
flag = false;
}
关于负号优化，如sin((-x)) = -sin(x) , cos(x) = cos((-x))，我的思路也是将factor toPoly 如果Poly的Unitlist 只有一项，就判断其系数是否为负，如果为负，则将Poly toString 后的结果乘上-1，并再次使用parser解析这个字符串获取newFactor。基于我的架构，这种优化有两个缺点，一个是cos((-1-x))若内部不止一项就无法提取负号了，一种是有的数据可能递归调用过多会卡tle 如sin(sin(sin(sin(sin(sin(sin(sin(sin(sin(-1))))))))))，所以我最后还是把这个优化注释掉了。
另外，一项的优化可能会导致其优化的结果可以和其他项继续进行优化，如sin(x)*3cos(x) + cox(x)*3sin(x) + sin(x)cos(x) ，最后的优化结果是sin((2x)),一个思路是可以判断优化后的输出结果是否变短了，如果变短了就继续进行优化。
另外，在这些优化中，普遍都调用了factor 的 toPoly方法，所以我觉得可以在存三角函数内部因子时候可以直接存储它的toPoly 形式，来提高性能。
Bug分析
自己程序的Bug
在二倍角优化上出了Bug，导致强测错了2个点，互测被刀了一次。我错误的将2*sin(x)*2cos(x)*2化为sin((2x))**2了，对能否进行二倍角优化的系数的判断没有处理好。
他人程序的Bug
找到了3个人的Bug,一个是Sin(0)**0的问题，一个是sin((-x))负号优化的问题，可见优化是很容易出错的，一定要谨慎(我只读了一个优化过的并且架构和我比较像的同学的代码，主要在找他的bug)。
第三次作业
这次作业支持求导操作,新增求导算子 ，乍看比较复杂，但实际写起来感觉应该是第一单元最轻松的作业了，在hw2上迭代开发2、300行就够了，主要精力放在了写评测机、检验正确性上，并未新增三角的优化，由于强测没寄，最后取得了90+的分数，也比较满意了。互测上，我没被找到bug，也没能找到别人的bug，可见经过前两次强测的轰炸，大多数bug已经被解决了。
心得体会
一个好的架构十分重要，可能每个单元的hw1是最难、最重要的，设计要具有可扩展性，在hw1中采用递归下降的算法去解析，用Poly去存储数据，后面作业只是在第一次作业上的增量开发，并没有重构。
测试很重要，感觉自己的代码水平一般，所以我每完成一个功能，都会捏造一些特定的数据去进行测试，在本地评测机跑代码时候，有时候反而希望多来几条出错的数据，每改好一个bug,心里才更有底。
关注讨论区很重要，在hw1 powPoly()方法中，我开始不知道怎样去进行深克隆，在同学的启发下才知道序列化、反序列化的方法。
有时候也不能在架构上花太多时间，有的问题单纯想很难想明白，可能代码一步一步写出来了思路会更清晰，想都是问题，去做才有答案。
...全文
请发表友善的回复…
发表回复