428
社区成员
发帖
与我相关
我的任务
分享BUAA OO UNIT1总结
前言
第一单元的作业中，主要学习了递归下降法解析一个表达式。并对表达式进行了简单化简。第一次作业本来不会递归下降，导致没有过公测，第二次作业使用递归下降重构，第三次作业增加了求导部分的开发。
第一、二次作业
由于前两次左右内容相似，这里合并到一起进行分析。
类图
注意：下方类图中的get和set函数做了适当省略。
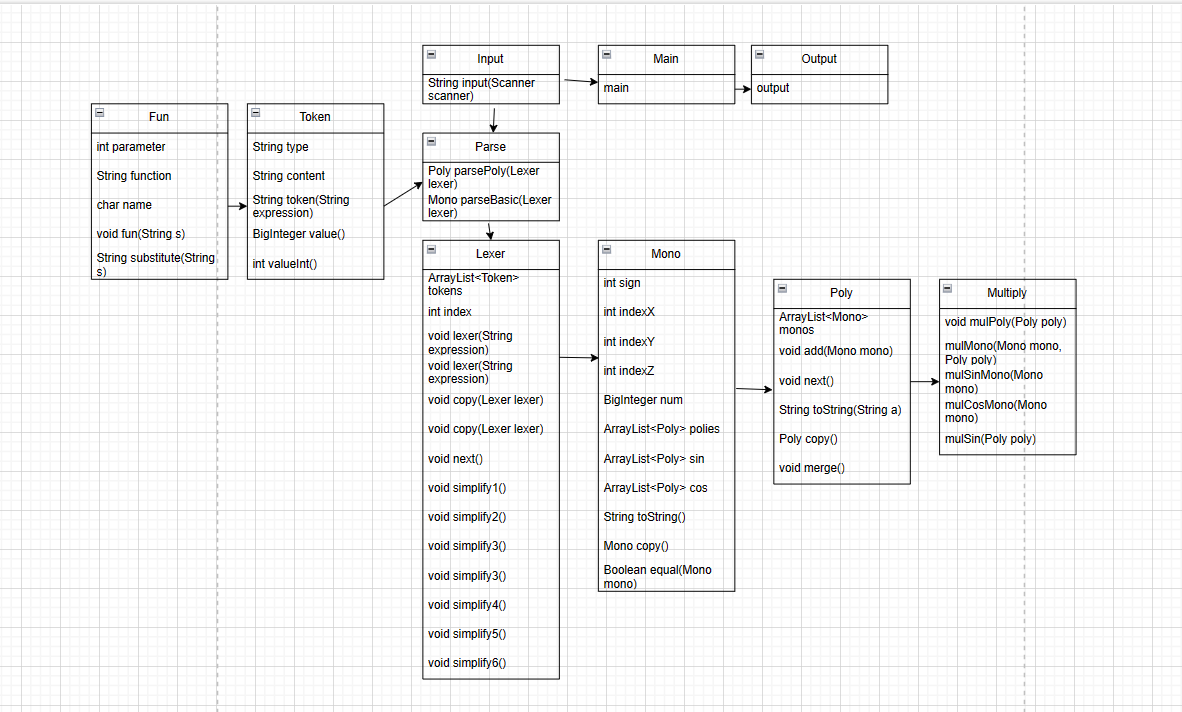
接下来简单介绍以下各个类的功能：
最中央是main函数，该函数通过调用input处理输入，经过解析计算化简最终通过output输出结果。
input类是输入类，第二次作业增加了自定义函数的输入功能。
output是输出类，通过传递进去一个toString字符串，可已经最终结果输出。
Fun是第二次作业新增的类，用于留存自定义函数，并在最终表达式中将自定义函数替换成一般表达式。
Token类保存了各种变量的解析形式。
Lexer类保存了一个表达式解析出来的各个变量。并且进行了简单化简，除去了将乘方转变为连乘的形式。
Parse类为解析器，将字符串解析为一个由变量组成的数组。
Mono类为单项式，在计算乘法之前，带括号的多项式也按单项式处理，保存在Mono类中。
Poly类为多项式，是一个由单项式数组组成的类，其中含有合并方法，可以用于后序化简。
Multiply类为一个计算惩罚类。将一个Mono中的乘法进行计算。
复杂度分析
一个图截不下了，这里分开截图：
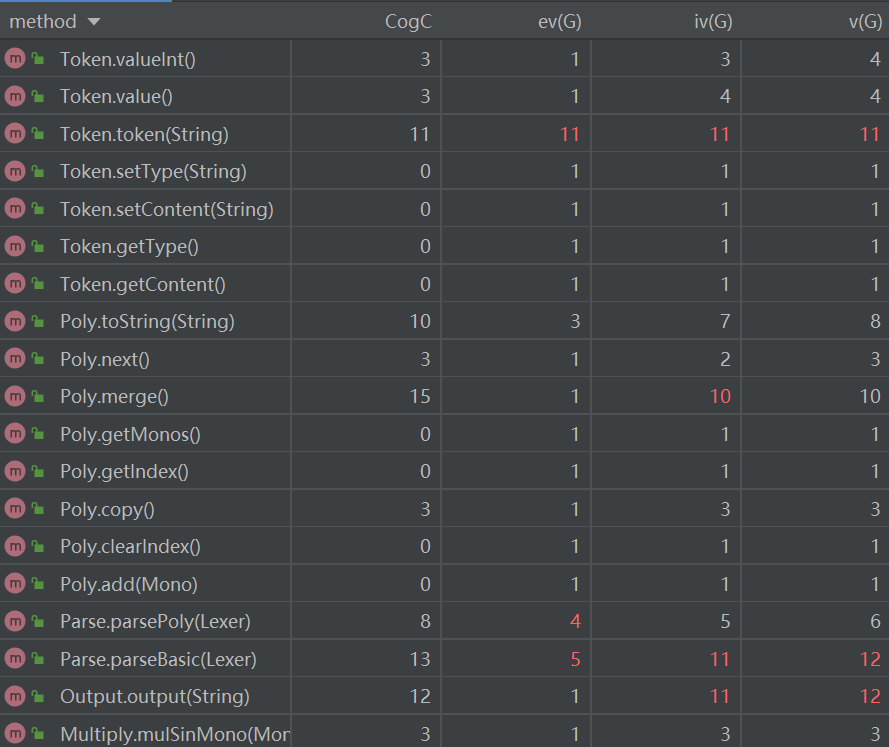
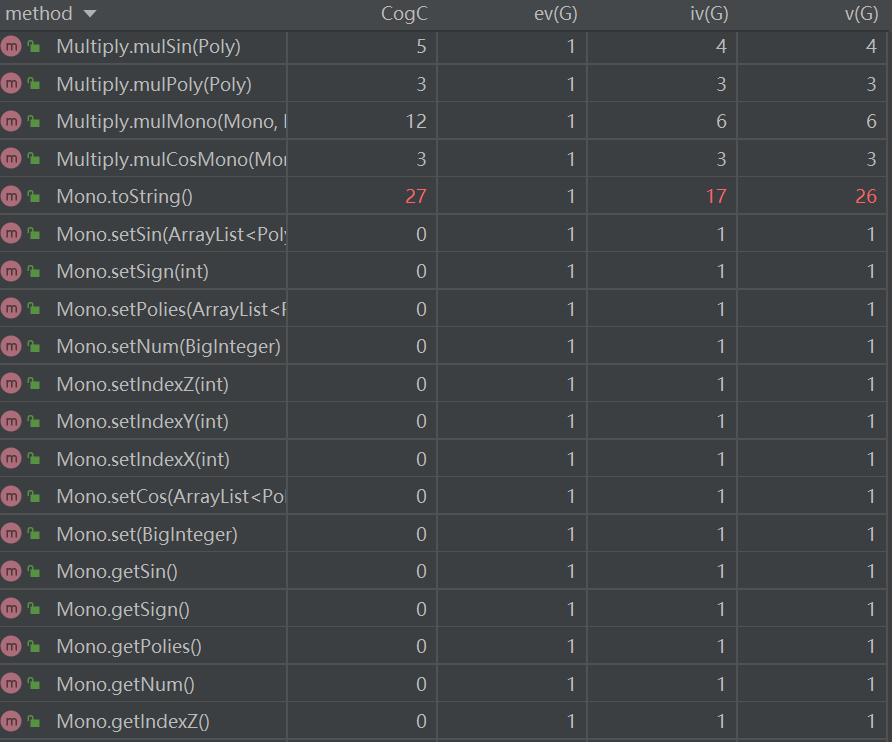
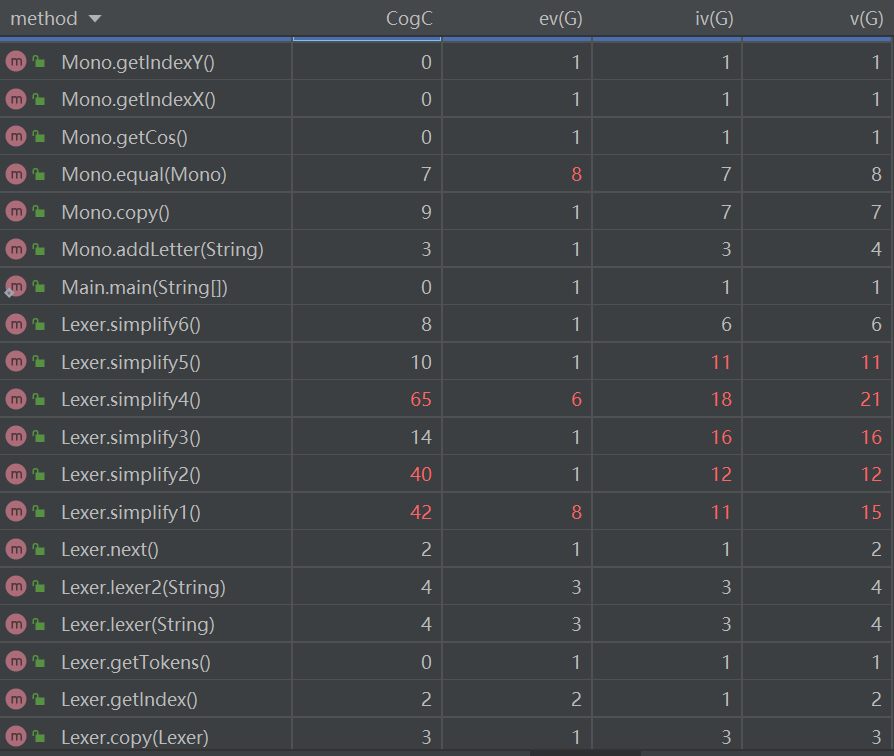
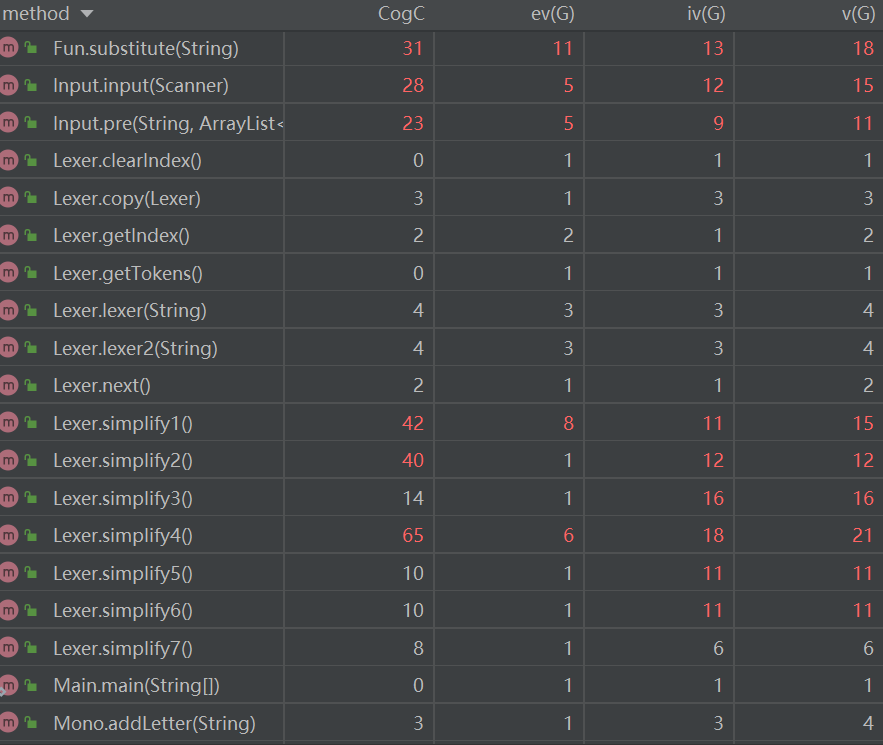
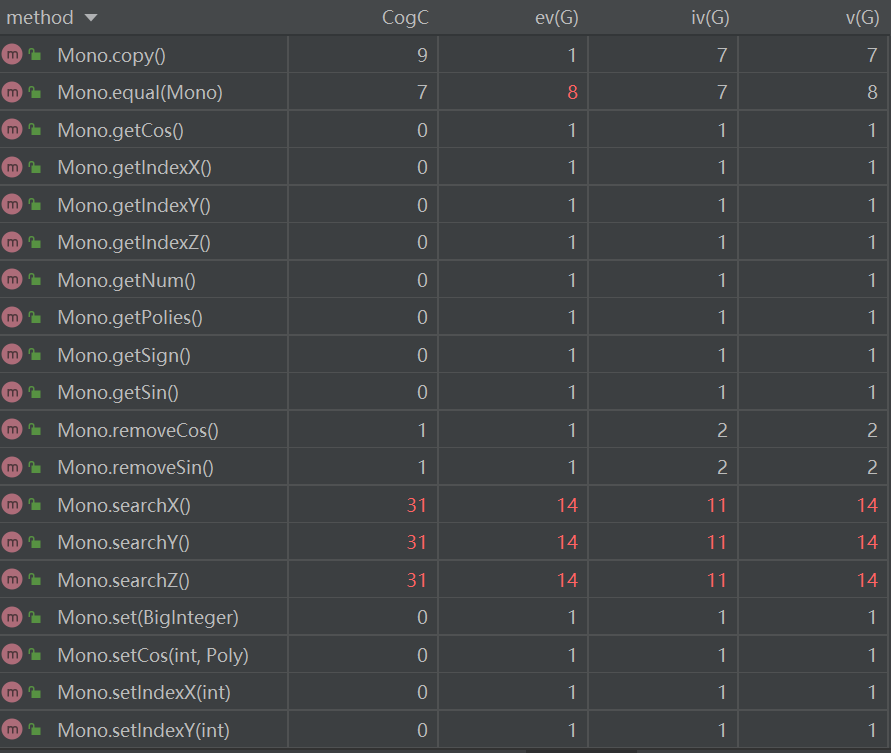
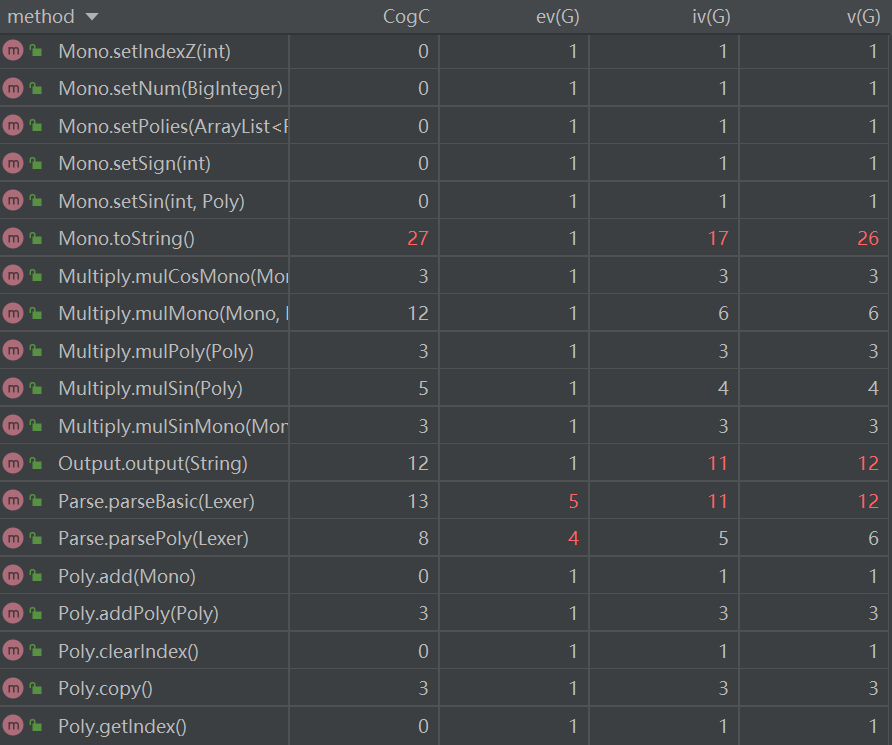
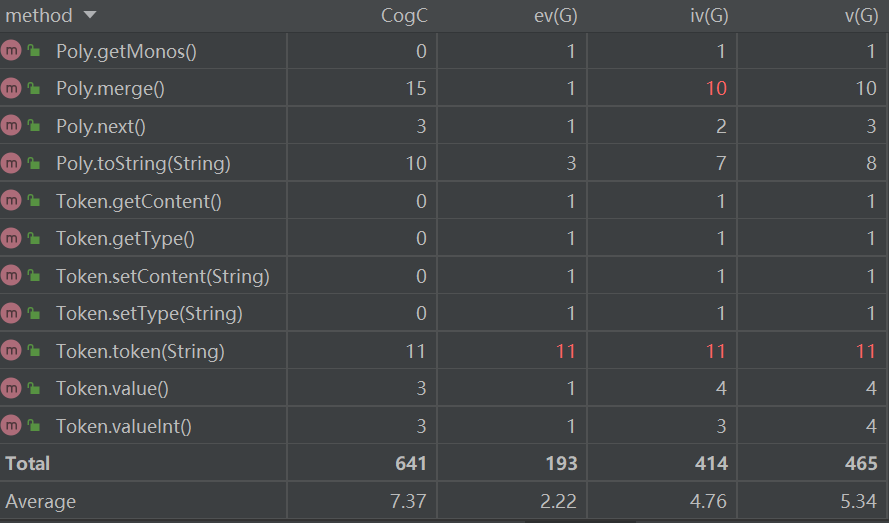
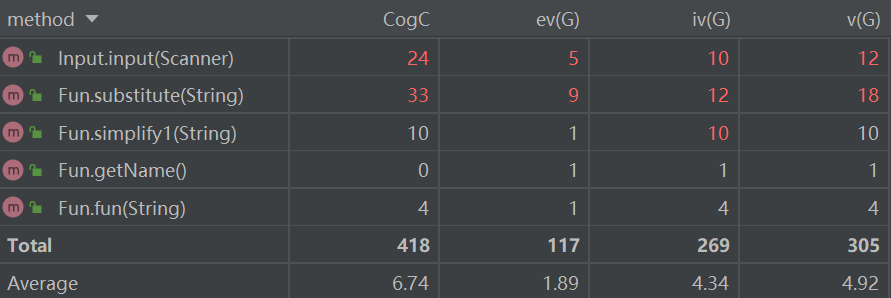下面分析一下复杂度较高的几个方法：
Token.Token:该方法需要遍历整个表达式字符串，并将每个字符与不同类型的变量进行比对，从而得出解析好的式子。
Parse.parseBasic:对基本的lexer进行遍历并得到一个基本的单项式。此处基本单项式为可能含有“（” + “多项式” + “）”的式子。
Output.output:由于该方法需要将传入的字符串再解析一边，故复杂度较高。
Mono.toString:判断了许多输出是可以减少输出长度的地方。并且还调用了Poly.toString
Lexer.simplify1:该方法用于去掉一个表达式中多余的括号，需要遍历整个表达式，然后找到一对括号，若其内层还有一对括号，则删去内层括号。
Lexer.simplify2 & Lexer.simplify4:用于将整个表达式中的乘方转化为连续相乘的形式。需要遍历表达式找到**，之后将找前面的乘方项，然后连乘。
Lexer.simplify3:用于除去一个表达式中存在的+-连续出现的情况。需要遍历表达式，找到+或-，然后判断下一个符号是不是+或-，如果是，则按照运算规则删去一个。
Lexer.simplify5:判断+、-前后出现非数字或变量的情况。
Input.input:因为输入数据可能存在自定义函数，在input中将自定义函数进行了替换，所以input的复杂度较高。
Fun.substitute:该函数就是将一个表达式的自定义函数替换成表达式的方法。因为需要遍历整个表达式，遍历到自定义函数是又需要便利自定义函数列表，所以复杂度较高。
Fun.simplify1:和Lexer.simplify3相同，处理+-连续出现的情况。
Bug分析
本代码出现了两个bug，下面对两个bug分别进行分析：
其一是在替换自定义函数时，忽略了一个函数可能存在若干空格的情况，只是直接读取了一个函数字符串第二个字符作为第一个自变量，并没有提前将一个字符串处理成无空格的形式。
bug修复在读入之后首先将所有空格除去：
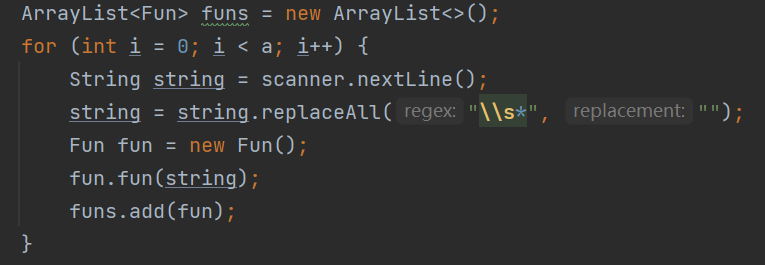
第二个bug是没有处理好一个+、-前后有括号或自定义函数的情况。这个bug的解决实在Lexer中增加了simplify5方法。
bug修复如下：
public void simplify5() {
if (tokens != null && tokens.size() > 0) {
for (int i = 0; i < tokens.size(); i++) {
if (tokens.get(i).getType().equals("minus") && i > 0 &&
tokens.get(i - 1).getContent().equals("*")) {
Token token3 = new Token();
token3.setContent("(");
token3.setType("leftBracket");
tokens.add(i, token3);
Token token = new Token();
token.setType("multiply");
token.setContent("*");
tokens.add(i + 2, token);
Token token10 = new Token();
token10.setType("rightBracket");
token10.setContent(")");
tokens.add(i + 2, token10);
Token token2 = new Token();
token2.setType("signed");
token2.setContent("1");
tokens.add(i + 2, token2);
} else if (tokens.get(i).getType().equals("minus") && i > 0 &&
tokens.get(i - 1).getType().equals("leftBracket") &&
tokens.get(i + 1).getType().equals("leftBracket")) {
Token token3 = new Token();
token3.setContent("(");
token3.setType("leftBracket");
tokens.add(i, token3);
Token token = new Token();
token.setType("multiply");
token.setContent("*");
tokens.add(i + 2, token);
Token token10 = new Token();
token10.setType("rightBracket");
token10.setContent(")");
tokens.add(i + 2, token10);
Token token2 = new Token();
token2.setType("signed");
token2.setContent("1");
tokens.add(i + 2, token2);
}
}
}
}
第三次作业
类图：
下方类图主要是作业增量开发时增加了Different类，用来给一个式子求导。
增量开发：
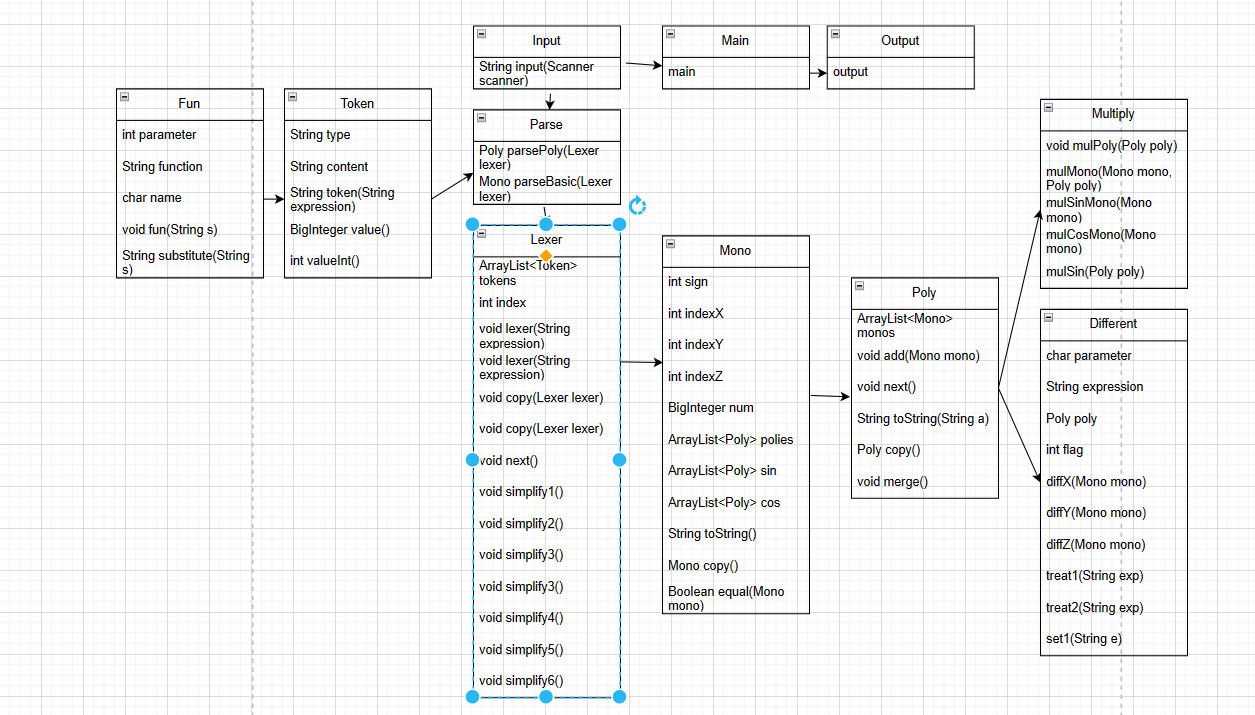
第三次作业相较于前两次增加了自定义函数之间的相互调用和求导。求导我增加了一个Different类。传递进去的是一个表达式字符串。字符串中如果含有"d"则判断该字符串中含有求导项，flag=1。之后将需要求导的项单独拿出来解析。记录求导变量（即该式是对谁求导）。然后调用求导的方法。求导方法中，三个变量分别对应了四个方法。每个方法解决表达式中无求导变量，有求导变量简单相乘或指数形式，三角函数形式，链式、符合求导形式。以x为例，下面附上对x求导的代码：
public Poly diff1(Mono mono) { //对x求导1
Poly poly1 = new Poly();
if (parameter == 'x' && !mono.toString().contains("x")) {
Mono mono2 = new Mono();
mono2.set(BigInteger.ZERO);
poly1.add(mono2); // 对x求导式子里没有x
} else if (parameter == 'x' && mono.toString().contains("x")) {
poly1.addPoly(diff2(mono));
}
return poly1;
}
public Poly diff2(Mono mono) { //对x的指数部分求导
Poly poly1 = new Poly();
Mono mono1 = mono.copy();
if (mono.getIndexX() != 0 && mono.getCos().size() == 0 &&
mono.getSin().size() == 0) {
mono1.set(mono.getNum().multiply(BigInteger.valueOf(mono.getIndexX())));
mono1.setIndexX(mono.getIndexX() - 1);
poly1.add(mono1);
} else if (mono.getIndexX() == 0 && (mono.getSin().size() > 0 ||
mono.getCos().size() > 0)) {
poly1.addPoly(diff3(mono));
} else if (mono.getIndexX() > 0 && (mono.getSin().size() > 0 ||
mono.getCos().size() > 0)) {
poly1.addPoly(diff4(mono));
}
return poly1;
}
public Poly diff3(Mono mono) {
Poly poly1 = new Poly();
for (int i = 0; i < mono.getSin().size(); i++) {
for (int j = 0; j < mono.getSin().get(i).getMonos().size(); j++) {
Mono mono1 = mono.copy();
mono1.getSin().remove(i);
mono1.setCos(0, mono.getSin().get(i).copy());
mono1.getPolies().add(0, diff1(mono.getSin().get(i).getMonos().get(j)));
poly1.add(mono1);
}
}
for (int i = 0; i < mono.getCos().size(); i++) {
for (int j = 0; j < mono.getCos().get(i).getMonos().size(); j++) {
Mono mono1 = mono.copy();
mono1.getCos().remove(i);
mono1.setSin(0, mono.getCos().get(i).copy());
mono1.setSign(- mono1.getSign());
mono1.getPolies().add(0, diff1(mono.getCos().get(i).getMonos().get(j)));
poly1.add(mono1);
}
}
Multiply multiply = new Multiply();
multiply.mulPoly(poly1);
multiply.mulSin(poly1);
poly1.merge();
return poly1;
}
public Poly diff4(Mono mono) {
Poly poly1 = new Poly();
Mono mono1 = mono.copy();
mono1.set(mono.getNum().multiply(BigInteger.valueOf(mono.getIndexX())));
mono1.setIndexX(mono.getIndexX() - 1);
poly1.add(mono1);
for (int i = 0; i < mono.getSin().size(); i++) {
for (int j = 0; j < mono.getSin().get(i).getMonos().size(); j++) {
Mono mono2 = mono.copy();
mono2.getSin().remove(i);
mono2.setCos(0, mono.getSin().get(i).copy());
mono2.getPolies().add(0, diff1(mono.getSin().get(i).getMonos().get(j)));
poly1.add(mono2);
}
}
for (int i = 0; i < mono.getCos().size(); i++) {
for (int j = 0; j < mono.getCos().get(i).getMonos().size(); j++) {
Mono mono2 = mono.copy();
mono2.getCos().remove(i);
mono2.setSin(0, mono.getCos().get(i).copy());
mono2.setSign(- mono2.getSign());
mono2.getPolies().add(0, diff1(mono.getCos().get(i).getMonos().get(j)));
poly1.add(mono2);
}
}
Multiply multiply = new Multiply();
multiply.mulPoly(poly1);
multiply.mulSin(poly1);
poly1.merge();
return poly1;
}
自定义函数之间的相互调用是在替换的时候解决的。一个自定义函数如果调用了之前定义的自定义函数，则先替换成表达式，然后再在计算的表达式中将所有自定义函数替换掉。
复杂度分析：
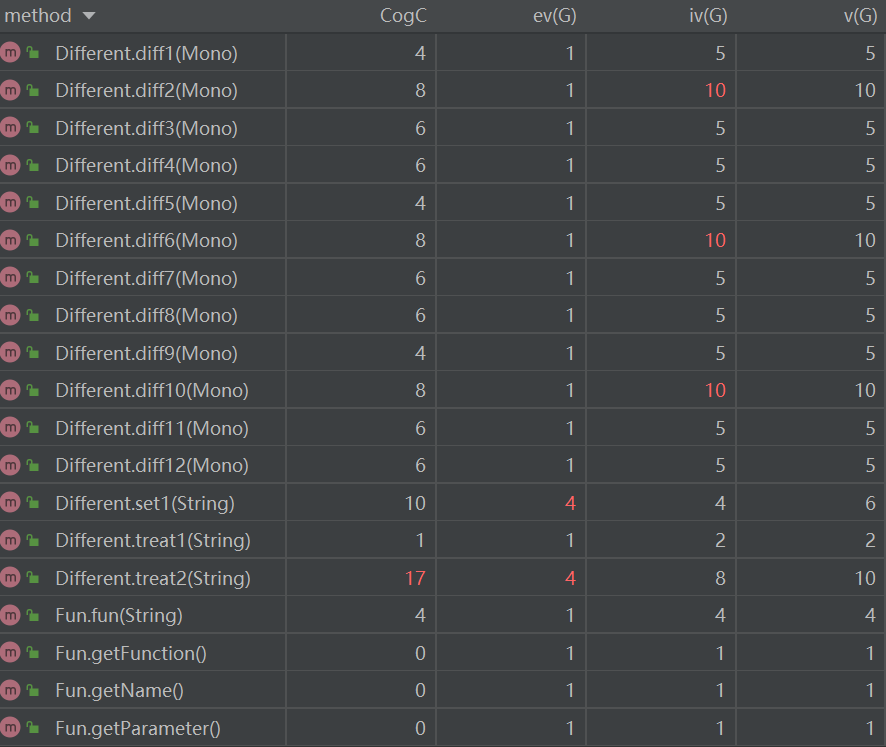
下面分析一下新增代码中复杂度较高的方法：
Different.diff2 & Different.diff6 & Different10:这三个方法出来求导变量换了以下，其余都一样 。这个方法是对一个式子求导，判断了是否有符合和链式求导。这个方法还调用了后续其他方法。故而复杂度高。
Different.treat2:该方法不仅调用了Different。diff1-12这12个方法，还调用了treat1，set1。
Bug分析：
本次作业又两个bug:
都是在求导过程中，对y,z求导的代码是复制的对x求导代码后稍作修改得到的，但是有的地方并没有修改完全，导致还是出现了两个小bug。
心得：
本单元的作业中，我最大的收获就是学会了递归下降算法。一个字符串可以通过一个解析器解析成不同类的项。并且该解析器由于递归调用，还可以支持嵌套。
P.S.以后写代码的时候如果遇到有些地方相似的时候，尽量不要复制粘贴，否则就会像第三次作业一样被迫de一些很难发现的bug。
...全文
请发表友善的回复…
发表回复
