BUAA_OO_2023 Unit1总结

[姚坤宜-20373355]

前言

OO第一单元的主题为表达式的括号展开，其基本架构在hw_1中建立，实现含有x、y和z变量多项式的单层括号展开，并支持四则以及幂运算。在后续迭代中，hw_2新增了三角函数因子sin和cos，其括号内能包含任意因子；新增了自定义函数因子，调用时传入因子作为参数；且支持括号嵌套。hw_3新增了求偏导因子，其括号内为表达式；定义自定义函数时能够调用已定义的函数。

总体而言，这次作业难度集中在前两次作业，在不重构的条件下，第一次作业的架构决定了后续迭代开发的思路和难度。于笔者个人而言，笔者并没有选上oo_pre作为先导课程，因此在本门课程开始时面向对象的思想极其浅薄，且尚未掌握java语言的基本语法，这都为第一次作业的架构构建到来了很大的困难。所以在此笔者要感谢一位朋友，他为笔者解决了java语法与数据结构的诸多疑问。谨以此贴，作为面向对象程序设计课程的新起点。

hw_1分析

训练目标：通过对表达式结构进行建模，完成多变量多项式的括号展开，初步体会层次化设计的思想

第一次作业第一单元之基石，既包含了针对本单元内容的递归下降思想的实践，也包含面向对象思想的基本建立。

架构分析

1. 递归下降——表达式树的建立

何为递归下降？我们先来仔细阅读本次作业的形式化描表述，可以发现被定义为如下形式：

表达式 ::= 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
项 ::= [加减 空白项] 因子 | 项 空白项 '*' 空白项 因子
因子 ::= 变量因子 | 常数因子 | 表达式因子

层次结构如下：

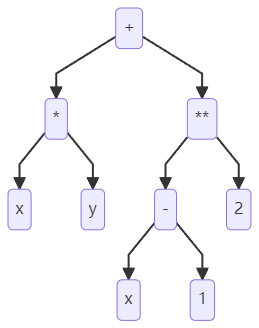
那在此次作业中，递归下降就可以表述为将表达式向下进行结构的拆分解析，并对得到的子结构递归进行上述过程，直到无法拆分。简单来讲，表达式即为项本身或项的加减运算，而项即为因子本身或因子相乘，呈现出严谨的层次结构；而表达式可通过添加括号成为因子，形成了一种闭环。既有层次，则下降解析之；既有闭环，则递归解析之。

在了解第一次作业表达式括号展开的需求后，笔者联想到了另外一种不含括号的表达式——后缀表达式。这是将操作符放在两个操作数后面的表达式，无需使用括号来保证表达式的计算顺序。而在得到后缀表达式时，除了使用栈以外，我们实际上还可以根据表达式建立表达式树，再对表达式树进行左序遍历得到后缀表达式。在本次作业中我们就可以在递归下降的解析中延用这种数据结构。

在此次作业中，我们有四种操作数：**{x, y, z, constant}，以及四种运算符：{+, -, *, **}**。因为运算符均为二元运算符，我们建立的表达式树也应当为二叉树，其结点为运算符或运算数。

下面以一个简单的表达式x*y+(x-1)**2（简称为E）为例解析。其表达式树如下所示：

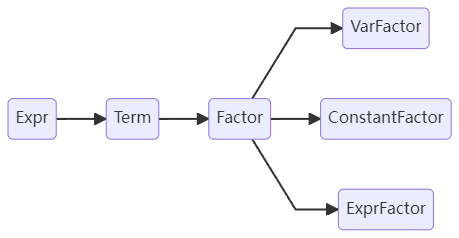
E是一个两项相加的表达式，左项为两个乘法因子相乘，右项为表达式因子与常数因子作幂运算。放在递归下降的过程中，我们先开启对表达式的解析。首先我们会解析到左项，则“下降”调用对项的解析；而项由因子构成，则再“下降”调用对因子的解析。解析完左项后，我们会解析到操作符“+”，这提示我们后面还有项我们继续项的解析。不同的是，这个项中含有表达式因子，那么我们会“递归”调用对表达式的解析。最终我们得以完成表达式树的构建。

结构类图如下所示：

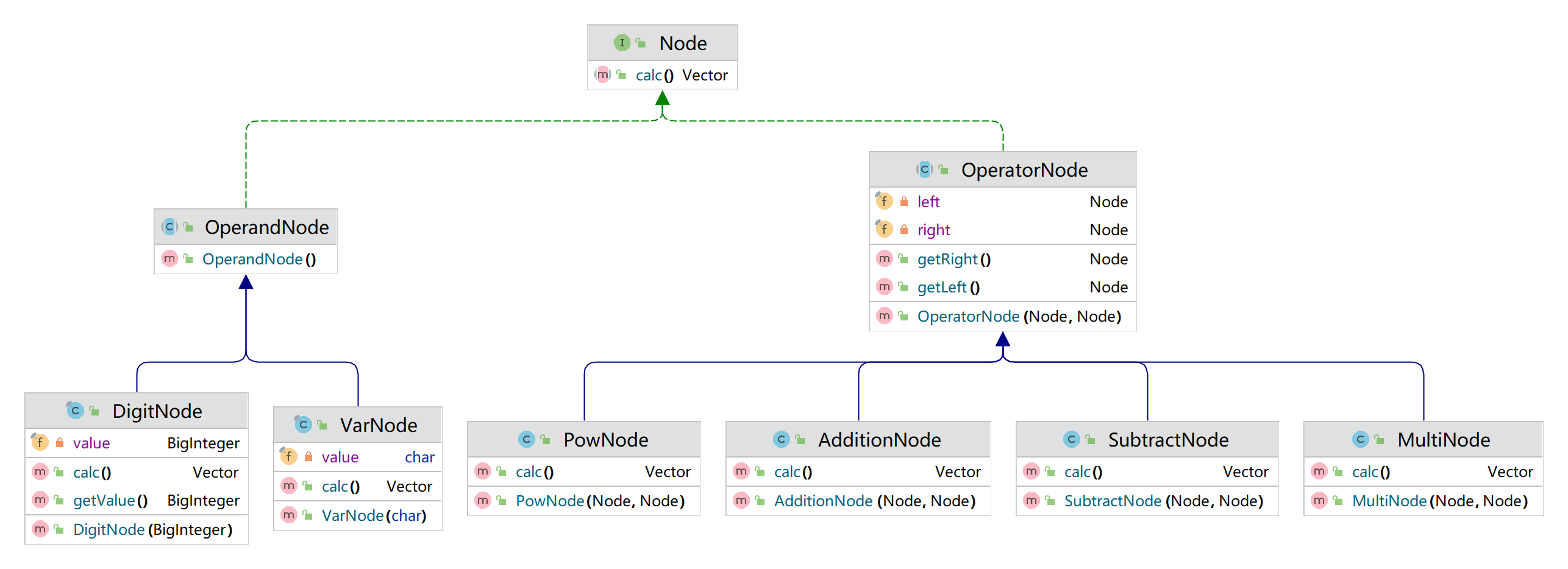
至此，我们完成了对表达式的解析。

2. 计算——归一化

对于括号展开后的结果，我们可以看作一个多项式。在数学上，多项式被定义为单项式的和，因此我们可以用单项式类型的ArrayList作为多项式结果。对于一个单项式，我们可以如此定义：

单项式 ::= constant * x**indexOfX * y**indexOfY * z**indexOfZ

index即为变量的指数，为0时则表明该单项式中不包含此变量，在数学上的结果就是1。

我们将从表达式树入手进行计算。对于每个操作符结点，它会向根结点返回自身左右叶子结点相运算的结果，其结果应当为一个多项式类。当这个结点在获取叶子结点的内容时，它的叶子结点也会递归调用上述过程，自顶向下。每进行一次结点计算，程序都应当新建一个多项式类，这个类的成员为叶子结点相运算的结果，由此返回给根结点，自底向上。最终我们会在整个表达式的根结点处获得最终的计算结果。

计算类图如下所示：

hw_2分析

训练目标：通过对表达式结构进行建模，完成多项式的括号展开与函数调用、化简，进一步体会层次化设计的思想。

迭代需求

1. 括号嵌套

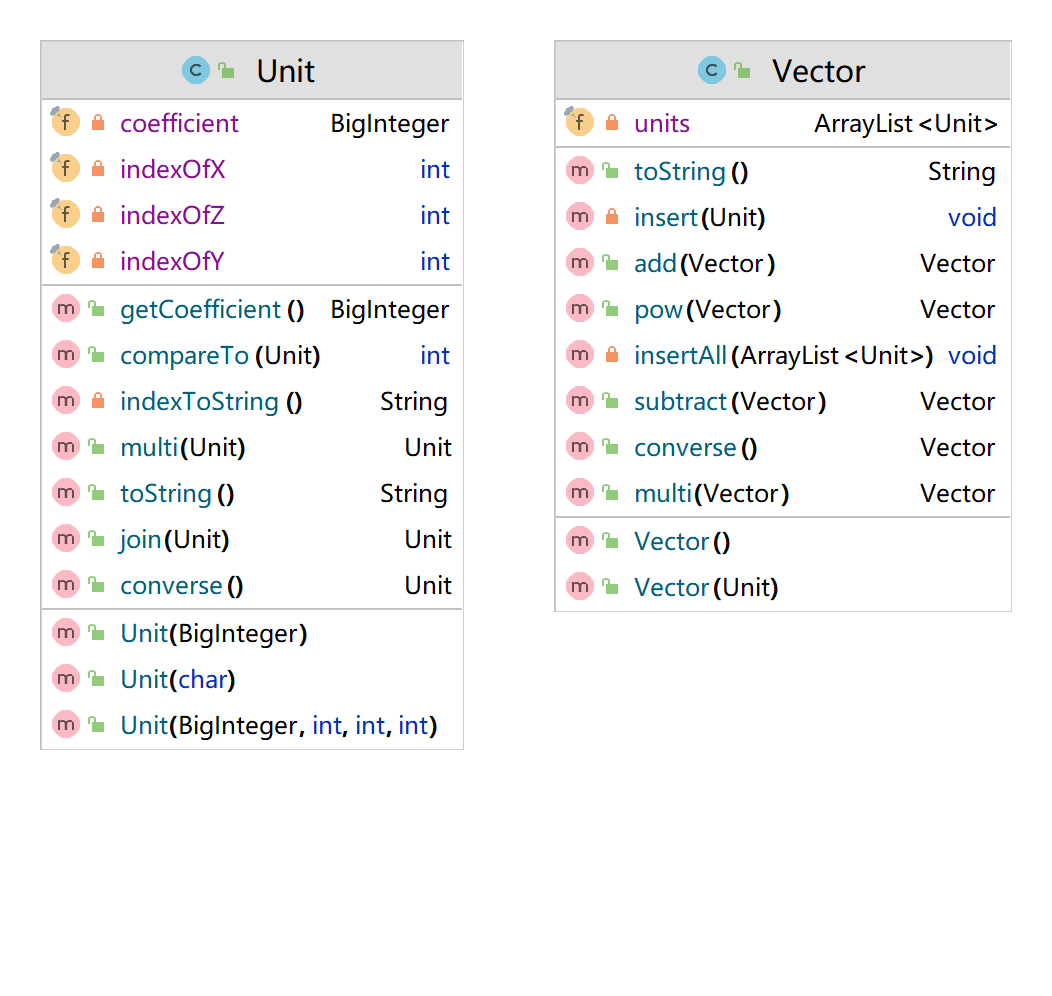
递归下降的方法能够解析出含有多层括号的表达式树，此需求已经在hw_1中实现。

2. 自定义函数

在hw_2中，我们可以在输入表达式前，自定义0 ~ 3个形如f(x, y, z) = 函数表达式的函数，函数的自变量为集合{x, y, z}的真子集。在调用时，自定义函数整体将被视为一个因子，传参形如f(因子, 因子, 因子)。对于自定义函数的处理，分为预处理和替换两步。

首先，对于预先自定义的函数，我们需要在解析表达式之前就对其进行处理，因此我们需要新增一个CustomizedFunc类，包含了函数名和函数表达式。对于后者，其本质就是表达式，因此我们可以直接调用词法分析器Lexer类和语法分析器Parser类，为自定义函数建立它的表达式树，并把它的根结点作为成员变量。

其次，当我们需要处理的表达式中含有自定义函数时，我们需要用各个因子替换掉原来的自变量，并将得到的新树接入表达式树中。那么我们在CustomizedFunc类中还需实现一个**substitute()**方法用于替换。

代码示例如下：

public class CustomizedFunc {
    private final char name;
    private final Node root;
    private final ArrayList<Character> varList;//记录定义函数时变量顺序

    public CustomizedFunc() {
        //构造方法
    }

    public Node substitute() {
        //替换方法
    }

3. 三角函数因子

三角函数因子的形式化表述为：**三角函数 ::= 'sin' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数] | 'cos' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数]**。显然，当我们在表达式中解析到三角函数因子时，对于它的内容，我们直接递归调用对因子的解析即可。

而在表达式树的建立中，三角函数实际上可以看作一种不同于hw_1中操作符的单目运算符。由于我们在hw_1中已经建立了一个Node接口，我们在本次迭代中只需要建立TriFuncNode抽象类，并用SinNode类和CosNode类继承。

TriFuncNode抽象类代码如下：

package node;

public abstract class TriFuncNode implements Node {
    private final Node content;

    public TriFuncNode(Node content) {
        this.content = content;
    }

    public Node getContent() {
        return content;
    }
}

SinNode类代码摘取如下：

public class SinNode extends TriFuncNode {
    public SinNode(Node content) {
        super(content);
    }

    @Override
    public Vector calc() {
        return new Vector(new Sin(getContent().calc()));
    }//Vector即为多项式类
}

归一化改进

由于新增了三角函数因子，我们最终得到的单项式结构也应当增加相应的三角函数。

设得到的单项式Mono为M，则可递归定义为：

M ::= constant * x**indexOfX * y**indexOfY * z**indexOfZ * sin((sum(M)))**index * cos((sum(M)))**index

其中**sum()**表示求和。

hw_3分析

训练目标：通过对表达式结构进行建模，完成多项式的括号展开与函数调用、化简，进一步体会层次化设计的思想。

迭代需求

1. 自定义函数的定义调用

本次作业函数表达式中支持调用其他“已定义的”函数，而在hw_2中，我们定义自定义函数时就已对其函数表达式进行了递归下降的解析，因此基本不用改动。

2. 求导因子

形式化表述中，对求导因子的相关定义如下：

求导因子 ::= 求导算子 空白项 '(' 空白项 表达式 空白项 ')'
求导算子 ::= 'dx' ｜'dy' ｜'dz'

我们可以仿照hw_2中对三角函数因子的处理，将求导算子视为单目运算符，新增DerivativeNode类实现Node接口，返回的，应当是其内容先计算再求导的结果。不过在此笔者并没有盲目地将'dx' 'dy' 'dz'建立为三个类，而是归于DerivativeNode类中，用成员变量记录求偏导的对象。

UML类图

度量分析

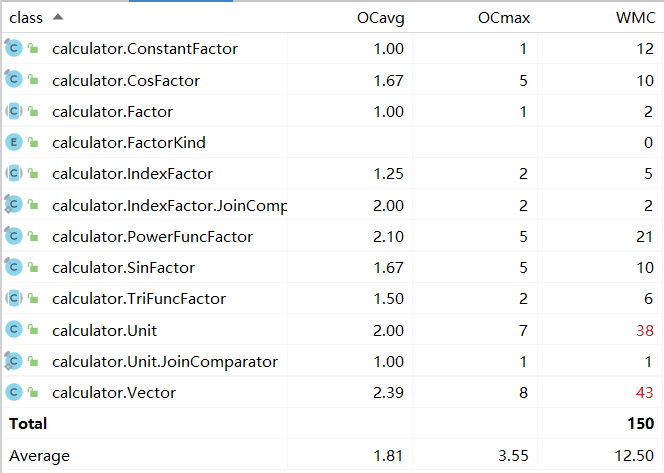
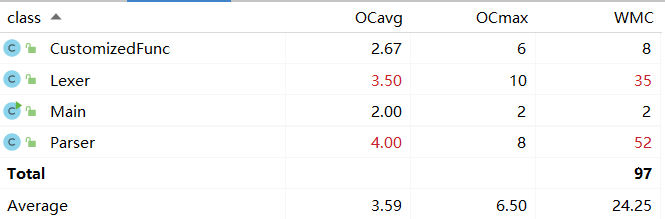
可以看出，Vector类和Unit类的复杂度较大因为它们承载了计算以及合并的功能；Parser类和Lexer类的复杂度也较大，因为它们承载了对表达式进行词法分析和语法分析的功能。

bug分析和hack策略

bug分析

在本次作业中，笔者的bug主要出现在Vector类和Unit类重写的toString()方法中。由于性能需求，若不对无关的项进行优化处理，那么我们最终输出的结果可能极其臃肿。若完全不优化，对例如**x这样的简单输入，可能得到1*x**1*y**0*z**0这样的臃肿输出，非常”不优雅“。因此笔者的bug往往出在化简中。例如，对于sin(x)+0这样的输入，由于对多项式的错误排序以及输出，导致程序并没有成功将多项式中的单项式0移除，再加上错误的符号输出判断，最终输出了sin(x)0。此外，在计算时笔者使用了BigInteger类储存常数，但在合并时比较系数的地方错误使用了getIntValue()方法**，埋下了数据溢出的隐患，最终被数据((8)**4)**8hack，实为不该。这个bug的根本错误在于类型的不匹配，以后应当多加注意。

hack策略

由于笔者能力有限，在第一单元中便没有独立写评测机，而是使用了大佬们放在评论区的成果。惭愧之余，也感谢大佬们的无私奉献。对于评测机跑出的bug，笔者选择逐渐对构造的输入进行精简，最终得到能够造成错误输出的最短输入，可以在一定程度上减小代价。

Unit1心得

总而言之，第一单元的学习对笔者来说是艰难和陡峭的，收获也是丰富的。

对笔者而言，最大的收获在于以下几点：java语法的掌握，递归下降思路的实践，面向对象思想和层次化设计的逐渐养成。

对于java语法的掌握，在课程开始时，笔者并未接触过java语言，因此对类、接口、方法等概念并不熟悉，也写出了许多荒唐的代码。而经过课下的学习与朋友的指导后，笔者从一个完全不知道StringBuilder类、不会使用parseInt()方法的小白，成长为了能够熟练运用各种java自带类的入门者，这是代码能力上的成熟。

对于面向对象和层次化设计思想的逐渐养成，犹忆荣哥在课上反复强调的话语：“想象你是在雇佣许多个程序员写代码。”在hw_2的迭代中，由于笔者层次化设计的的思想还很浅薄，笔者选择了在程序入口，也就是Main.java中，用字符串替换的方式处理掉自定义函数，并将替换后的字符串进行处理。这条歧途也导致了笔者没有按时完成hw_2，提交了无效作业。因此笔者在后来新建CustomizedFunc类，将自定义函数的处理交给了这个新的“程序员“，最终完成了hw_3的迭代开发。

希望第一单元能够成为笔者的一个新起点吧。共勉。