444
社区成员
发帖
与我相关
我的任务
分享BUAA-OO-第一单元总结
第一次作业
设计思路
题文要求将输入的表达式展开输出，同时在性能分要求上潜藏了对于展开后的表达式进行同类项合并等缩短输出长度操作的要求。可以根据此将本次作业分为两个主要部分，第一部分是处理输入的表达式，第二部分是根据处理得到的信息输出优化结果。
第一部分，处理输入的表达式
基于所给的文法规则，笔者使用了递归下降的思想来处理表达式。
首先注意到在文法规则中存在大量的空白符信息，而空白符对于递归下降的处理过程其实是没有太多影响的，反而会因为如果在处理过程中不断判断空白符的出现与否导致分支语句的复杂程度上升，因此首先将输出的表达式进行预处理，将其中所有规定的空白符全部去除。
String exp;
exp = scanner.nextLine();
//去掉所有空格
String expnew = new String("");
for (int i = 0; i < exp.length(); i++) {
if ((exp.charAt(i) != ' ') && (exp.charAt(i) != '\t')) {
expnew += exp.charAt(i);
}
}
随后根据给定的文法规则，将所有的左递归文法进行适当改写之后，再根据统一改写后的文法规则设计类及其属性和方法。
在通过此设计后，通过递归下降可以将整个表达式信息处理为树状结构。
// 改写文法
// 表达式 → [加减] 项 { 加减 项 }
// 项 → [加减] 因子 { '*' 因子 }
// 因子 → 变量因子 | 常数因子 | 表达式因子
// 变量因子 → ('x' | 'y' | 'z') [指数]
// 常数因子 → [加减] ('0'|'1'|'2'|…|'9'){'0'|'1'|'2'|…|'9'}
// 表达式因子 → '(' 表达式 ')' [指数]
考虑到需要存储从输入表达式中获取到的信息，额外设计数据信息类，将所有需要的内容用该类存储下来，进一步而言，在该次作业中，所有的项都可以归类为常系数C乘以X、Y、Z变量幂次的形式，因此将常系数C及X、Y、Z变量的指数作为数据信息存下即可满足需要。
同时考虑到在处理后续的数据计算时，可能会涉及到大整数的相关计算，因此在此处就将相关信息用_BigInteger_来进行存储，避免一些不必要的麻烦。
public class Cxyz
private BigInteger cint;
private BigInteger xint;
private BigInteger yint;
private BigInteger zint;
第二部分，输出优化结果
根据先前第一部分处理表达式获取到的信息来进行结果数据及优化。
首先依然是根据文法规则，在原先设计的类的基础上增添新的方法，这些方法直接利用类属性中的信息来进行结果输出，例如对于表达式因子内部而言是处理加减，对于项因子内部而言则是处理乘法，其他的处理部分大同小异。
// 表达式 → [加减] 项 { 加减 项 }
public ArrayList<Cxyz> getCxyzs() {
cxyzs = xiang.getCxyzs();
if (jiaJian.equals("-")) {
for (int i = 0; i < cxyzs.size(); i++) {
cxyzs.get(i).setC(cxyzs.get(i).getC().negate());
}
}
for (int i = 0; i < xiangs.size(); i++) {
ArrayList<Cxyz> cxyzsAdd;
cxyzsAdd = new ArrayList<Cxyz>(xiangs.get(i).getCxyzs());
if (jiaJians.get(i).equals("-")) {
for (int m = 0; m < cxyzsAdd.size(); m++) {
cxyzsAdd.get(m).setC(cxyzsAdd.get(m).getC().negate());
}
}
cxyzs.addAll(cxyzsAdd);
}
return cxyzs;
}
// 项 → [加减] 因子 { '*' 因子 }
public ArrayList<Cxyz> getCxyzs() {
cxyzs = yinZi.getCxyzs();
if (jiaJian.equals("-")) {
for (int i = 0; i < cxyzs.size(); i++) {
cxyzs.get(i).setC(cxyzs.get(i).getC().negate());
}
}
for (int i = 0; i < yinZis.size(); i++) {
ArrayList<Cxyz> cxyzsmul0;
ArrayList<Cxyz> cxyzsmul1;
cxyzsmul0 = new ArrayList<Cxyz>(cxyzs);
cxyzsmul1 = new ArrayList<Cxyz>(yinZis.get(i).getCxyzs());
cxyzs = new ArrayList<Cxyz>();
Cxyz mulres;
for (int j = 0; j < cxyzsmul0.size(); j++) {
for (int k = 0; k < cxyzsmul1.size(); k++) {
mulres = new Cxyz();
mulres.setC(cxyzsmul0.get(j).getC().multiply(cxyzsmul1.get(k).getC()));
mulres.setX(cxyzsmul0.get(j).getX().add(cxyzsmul1.get(k).getX()));
mulres.setY(cxyzsmul0.get(j).getY().add(cxyzsmul1.get(k).getY()));
mulres.setZ(cxyzsmul0.get(j).getZ().add(cxyzsmul1.get(k).getZ()));
cxyzs.add(mulres);
}
}
}
return cxyzs;
}
在处理完所有的表达式信息后，可以最终得到一个初步的表达式输出结果，但是仅仅将此信息完整的不做处理的输出，其结果长度还是不能让人满意的，因此针对于此需要进行输出的额外处理。
主要是同类项的合并，针对于X、Y、Z变量幂次完全相同的单元进行合并，此时仅仅需要涉及加减运算。
for (int i = 1; i < cxyzsold.size(); i++) {
int j = 0;
for (j = 0; j < cxyzs.size(); j++) {
if (cxyzsold.get(i).getX().intValue() == cxyzs.get(j).getX().intValue()) {
if (cxyzsold.get(i).getY().intValue() == cxyzs.get(j).getY().intValue()) {
if (cxyzsold.get(i).getZ().intValue() == cxyzs.get(j).getZ().intValue()) {
cxyzs.get(j).setC(cxyzs.get(j).getC().add(cxyzsold.get(i).getC()));
break;
}
}
}
}
if (j == cxyzs.size()) {
cxyzs.add(cxyzsold.get(i));
}
}
其次是一些对于输出细节的考量，比如说常系数C为0时且后续没有其他单元时直接输出0，常系数C为1且X、Y、Z变量幂次全为0时输出1，常系数C为1且X、Y、Z变量幂次不全为0时将常系数1输出省略。这些输出细节的考量也是决定性能优劣的重要部分，因为处理考虑的部分较为的繁琐多样，故而在此省略对于此部分的代码展示。
类图
度量分析
第二次作业
迭代思路
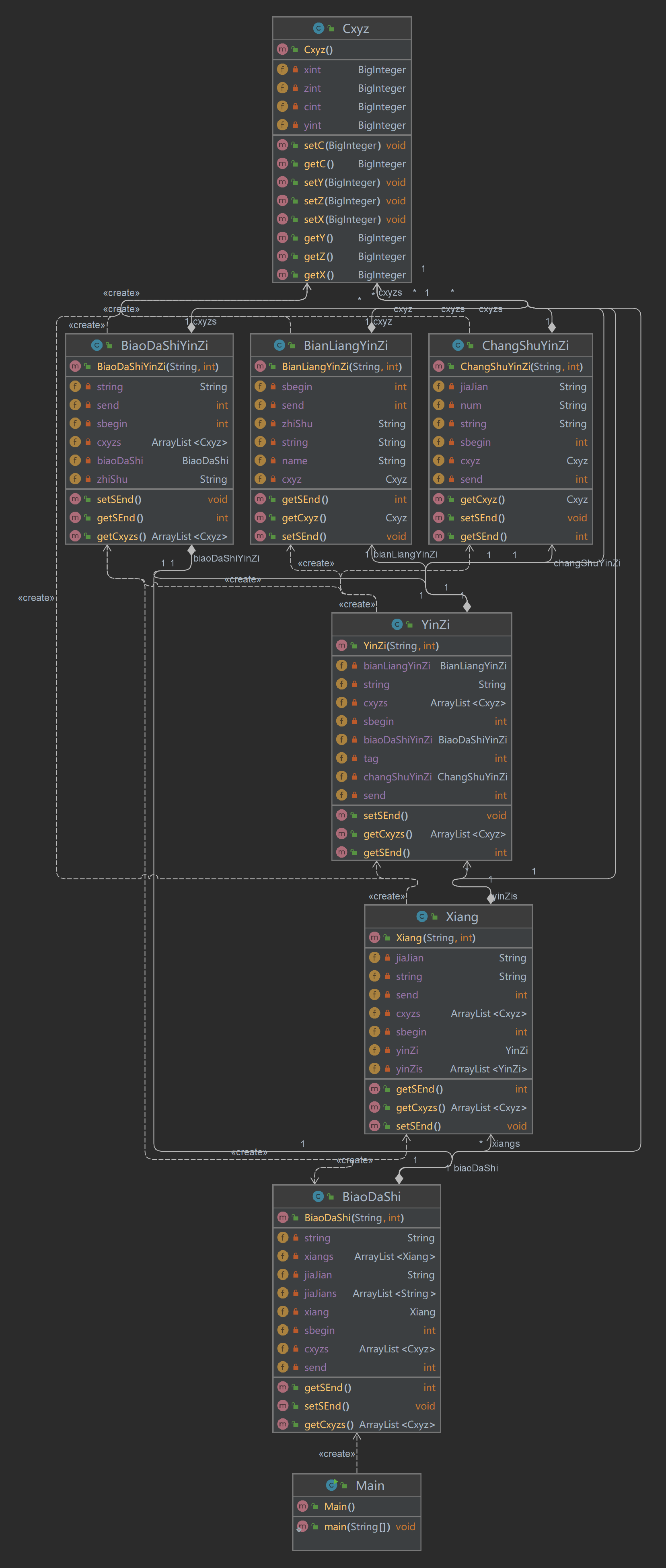
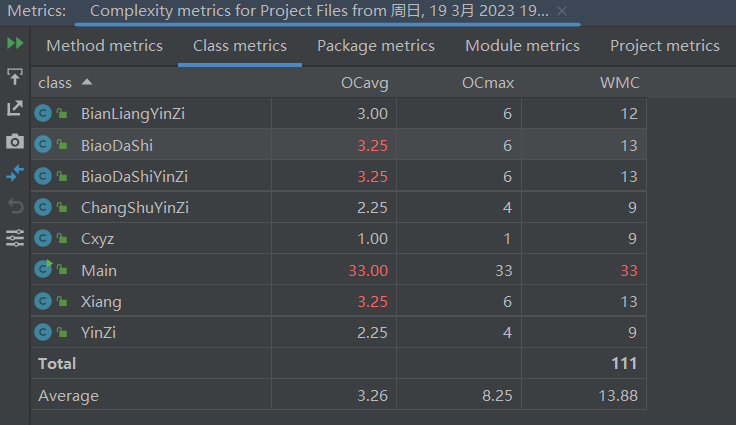
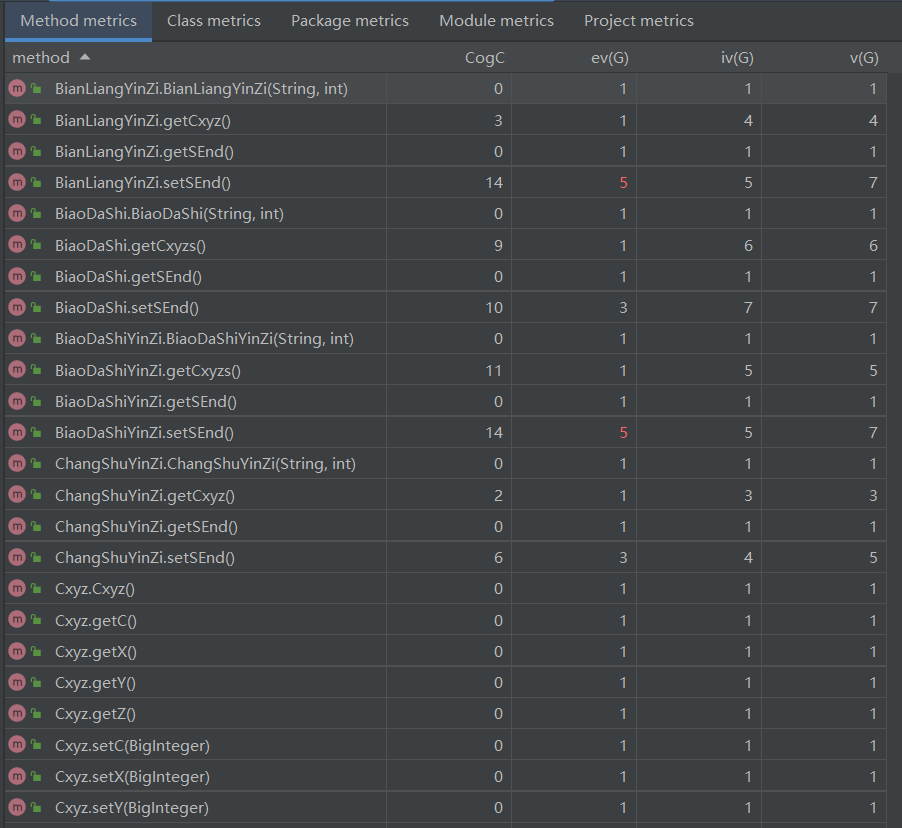
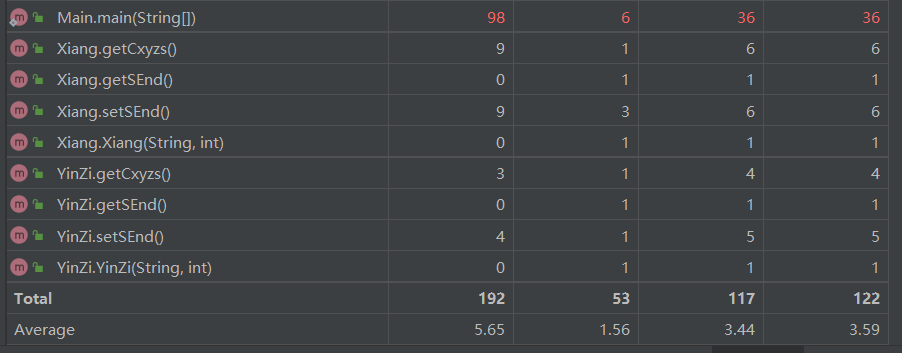
采用了递归下降的方法处理第一次作业，因此该部分也无需进行大规模的重构设计，简单总结一下。
第二次作业引入了对于括号的叠加以及三角函数因子的考量。括号的叠加对于递归下降的方法而言没有影响，唯一需要考虑的是三角函数因子，对于三角函数而言其影响着两个部分。第一部分是架构设计，因为文法上的变动需要进行一些类的迭代，第二部分是表达式输出，三角函数在数学上具有的诸多性质带来了表达式化简上的难度，笔者在该部分的原有思路不成熟，因此没有很好的处理这部分的性能。
在研讨课上针对三角函数表达式化简思路上有了一些启发，例如说将sin函数形式全部统一利用平方和公式转化为cos函数形式，然后再进行化简，同时在利用这种思路时，可以首先记住转化处理前的表达式长度，以及最后处理得到的表达式长度，然后二者取其短进行输出。
第三次作业
迭代思路
第三次作业引入了对于函数的定义和求导规则，主要是带来了文法上的改变，因此主要集中在对于第一部分的迭代处理。
求导规则对架构的影响不大，只是在架构上需要独立设置一个求导相关的类，主要用于处理求导所用的求导规则，将这些规则封装成对应的方法，就可以在表达式处理过程中完成相关的工作。
函数的定义的引入最初笔者考虑的是建立函数表，将函数表以及待处理表达式一同传入，在处理过程中通过不断查表来处理，但是在后续的实现过程中发现这种思路带来的复杂度很高，因此摒弃了这种方法。通过在讨论区学习其他同学的思路发现，其实对于函数的定义可以简单考虑为这么几步，第一步是将定义的函数作为一个表达式先做化简处理，第二步在表达式输入环节直接进行代入处理，这样整个表达式就回到了第二次作业需要处理的层次，只是多出了对于求导的处理分析。
BUG分析
在总体单元作业中的设计中遇到的最为严重的BUG应该是深浅拷贝的问题，实际上还是因为自己对于java语言的使用还是有很多不到位的地方，不过好运的是这个问题在公测时就能够即使的发现并解决。
在自测及互测阶段，笔者没有程序化设计评测工具的能力，因此更多的是人为的设计一些测试数据来进行分析，主要的是从两个方面进行考虑。第一个是考虑边界，例如在第二次作业中涉及对括号嵌套问题的处理时，设计很多相关的括号数据，以此来分析自己和他人的方法是否在该处考虑到位。第二个是压力测试，比如作业中要求的指数最高为8，那么在测试环节，将一些指数调整到8看是否会TLE。
心得体会
本单元主要是对于java基础语法的考量以及如何从原先的面向过程的思维转化为面向对象的思维的考验，当然，就该次作业的工作量而言，确实还是挺大而且具有挑战性的，不过这样的经历也同样是对于同学们的宝贵经验，如何在压力中前进，并且不断学习进步和挑战自我，不仅仅是一门课程应有的态度，其实也是面对今后未来生活应有的态度。很可惜的是，笔者作为该课程的重修生，在早期的学习中并没有认识到这一点，反而总想着如何轻松和逃避，只是希望现在能够认识这一点还不算晚，望读者能观笔者有所感。
...全文
请发表友善的回复…
发表回复
