BUAA-OO 第一单元作业
前言
第一单元的主题是计算表达式,这包括拆括号+合并同类型两部分。主要的学习目标是熟悉面向对象的思想,用递归下降法解析文法,学会使用类来管理对象,掌握一定的模块化设计能力。本单元一共有三次作业
- 含x,y,z变量的表达式计算
- 含有三角函数、自定义函数且支持多层括号嵌套的表达式计算
- 含求导因子的表达式计算
可以看出,这三次作业的要求是一步步递进的,代码的复杂度也同样大大递增。为了避免不必要的重构,我们需要在一次作业就构思好一个可扩展性强的架构。本人第一次作业耗时最长,毕竟从零开始搭建是最难的一步,在后续迭代过程中,好的架构帮助我节省了很多的时间,让我每次写作业的时间呈几何式递减,第三次作业甚至只写了一个小时就完成了。借着这篇博客作业,我将对三次作业的代码与架构进行详细分析,并总结面向对象的学习心得。
UML类图
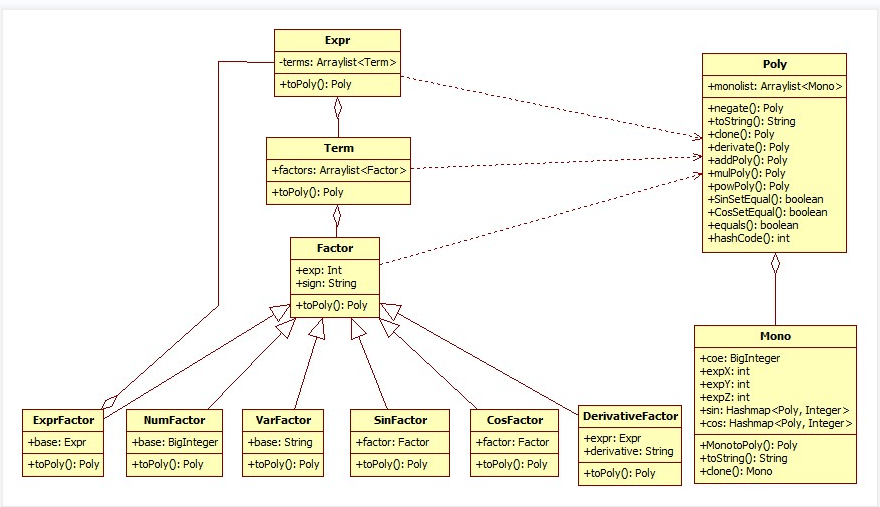
第一次作业
第一次作业主要是关于多变量多项式的展开,这次我们需要展开的表达式中因子只有三种——幂函数因子,常数因子和表达式因子。
架构分析
建类的逻辑很简单,难点在于如何实现展开。
- 首先分析展开后的形式:poly=∑coe*var**exp
为了储存展开后的该形式我们需要建立两个类——Poly(多项式)和Mono(单项式)
Poly类有一个ArrayList容器,用来容纳一系列数组元素Mono。 - 其次分析实现展开的方法,这也是最核心的一步。对于一个expr,因其形式的多元性和factor内容的随机性,我们对它的展开可能毫无头绪,这里有个很好的思路就是:递归思想
- 展开一个expr为多项式很难,那不妨先将最简单的factor进行展开,例如numfactor,varfactor。
- 再往上一层实现term的展开方法,这里通过定义两个多项式相乘的函数,使得term可以通过先调用factor的展开,再调用多项式相乘,从而实现term展开为多项式的方法。
- 再往上一层实现expr的展开方法,同样的通过定义两个多项式相加的函数,使得expr可以先调用term的展开,再调用多项式相加,从而实现expr展开为多项式的方法。
- 至于exprfactor则可调用expr的展开方法作为其展开的方法
- 这里我们将各类展开为多项式的方法统一起名为toPoly(),在基类factor中定义toPoly()空函数,其子类重写父类该方法,便于展开过程中利用好面向对象里的多态。
- 故在main函数里只需写expr.toPoly()一行代码即可递归调用各层次的toPoly()函数,完成expr向Poly的转化。
与其他架构相比的优点
- 直接实现了多层括号的嵌套
- 递归调用避免了直接用for循环实现拆括号时需要判断factor类别而实现不同的乘法方法。
- 有很强的可扩展性,且十分规范,迭代新增一类因子只需实现其toPoly()函数,即可融合到原先版本中。
第二次作业
第二次作业主要是关于含有三角函数、自定义函数且支持多层括号嵌套的表达式展开,这次我们需要展开的表达式中因子只有5种——幂函数因子,常数因子,表达式因子,sin因子,cos因子。
架构分析
本次新增的的内容可分为两大部分:
- 自定义函数
- 思路是先将自定义函数进行代入,采用的是字符串层面上的替换,函数代入后再调用expr.toPoly
- 具体分为三步:自定义函数的存储、调用时的传参、调用完成后嵌入原表达式
- 首先是自定义函数的储存:由于函数名和函数体挂钩,很自然的想法是用Hashmap<函数名,函数体>来存储,key为函数名,value为函数体
- 其次是调用时的传参:很直观的思路是用replace函数进行替换,如f(x,y) = x + y调用时expr = f(y,1),但这样由于传参的非同步性会导致结果为2而非正确结果y+1,固可采用导入MessageFormat格式化模式包,实现同步传参。或者可用取巧的方法先将函数体中x,y,z转为q,w,e(var不会出现的字母),这样也可避免该问题。但建议用前者,因为后者不符合可扩展性要求。
- 最后是调用完成后嵌入原表达式,需注意f(x) = x+1 expr = 3*f(x), 直接嵌入会变为3*x+1而非3*(x+1),固需注意再嵌入前先用()将f(x)包住。
- 三角函数因子
- 由于三角函数因子的存在,我们需要重构一下Mono的成员,不难想象展开后的单项式(即最小单元)统一形式应为 coe*x*exp∏sin(Factor)**exp * ∏cos(Factor)**exp
- 随之而来的问题是,在加法函数中进行的合并同类项操作如何判断是同类项,这里采用重写poly的hashcode和equals方法进行正确的两个poly相等的判断,巧妙的是,在equals方法中我采用的是:调用两个poly相减的函数再判断结果是否为0的方法进行判断,这样即可递归调用至最底层实现多层嵌套的sin内因子相同的判断。
第三次作业
第三次作业主要是关于含求导因子的多项式展开,这次我们需要展开的表达式中因子只有6种——幂函数因子,常数因子,表达式因子,sin因子,cos因子,求导因子。
架构分析
有两个新增要求,第一是有求导因子dx、dy、dz,第二是自定义函数在定义时可以调用先前定义好的自定义函数。
- 新增求导因子,并在Poly类实现求导函数,很容易,需要注意的是sin类求导后变为cos类需要判断是否与原有的cos相同,相同则指数相加。
- 第二个要求我是在读入自定义时调用了自定义的代入,即边定义边调用,这样可解决该需求。
度量分析
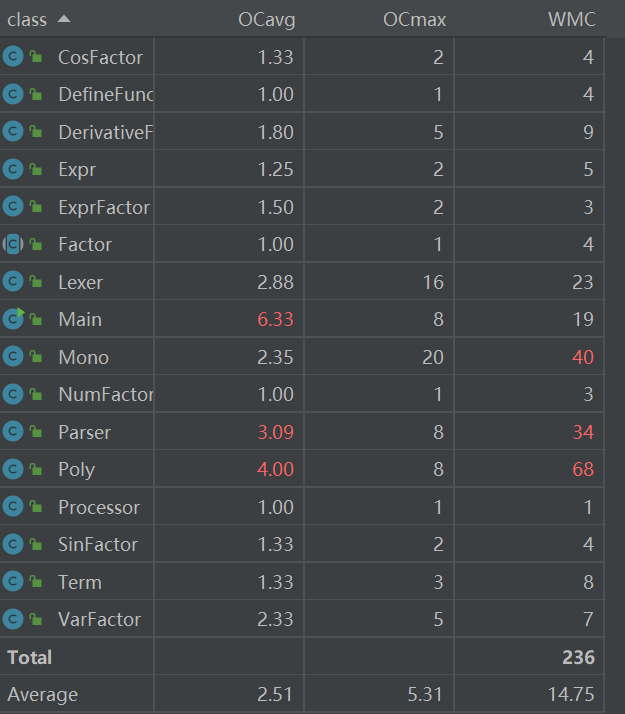
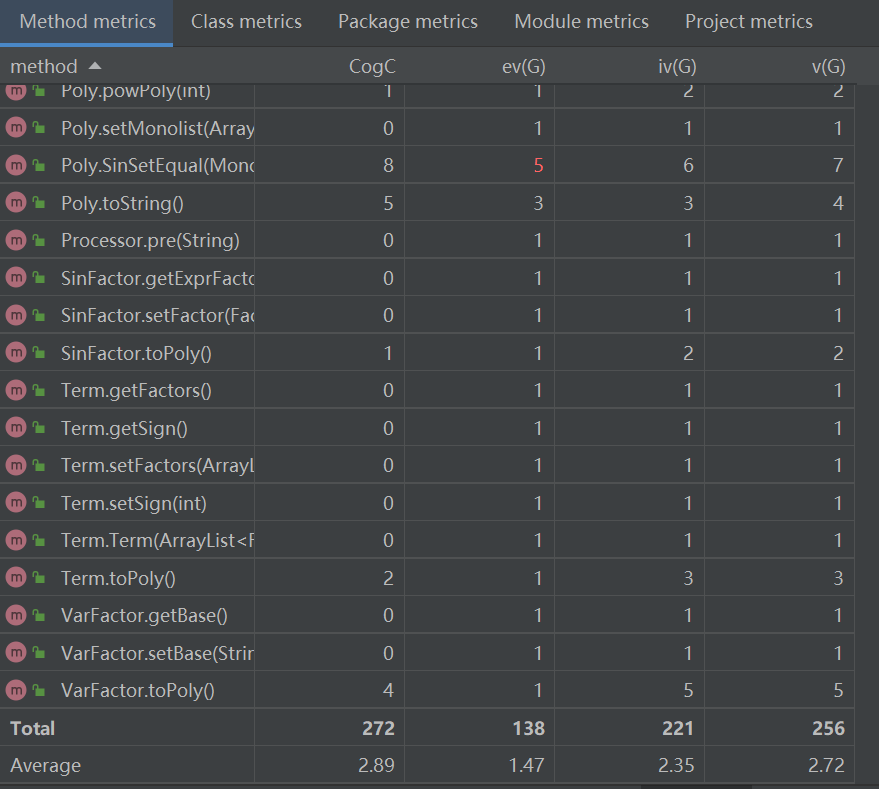
类的方法平均复杂度不高,不过 toString() 方法在 Cogc, ev(G), iv(G), v(G) 等多个复杂度度量方式下都有较高的值
这是因为在 toString() 方法有判断增加了逻辑分支,导致程序流程图比较复杂,耦合度较高。
Mono类中增加了sin,cos等新的数据成员,导致在输出时判断逻辑更为复杂,同时也直接导致了Poly类中进行add和mul运算时进行的操作也更为复杂。
强测互测BUG分析
对1*x优化为x时直接采用replace进行的优化,导致例如21*x会被优化为2x,产生错误,后修复bug采用coe判断为1,进行优化,可见字符串层面replace很容易产生问题,应谨慎使用。
学习心得
熟练掌握了parser、lexer进行文法词法分析的递归下降法,学到了递归toPoly解决问题的算法思想,以及面向对象多态继承封装三大特性的深入理解。
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享

