382
社区成员
OO 第一单元作业总结
前言
任务：对输入表达式结构建模，完成多项式的括号展开与函数调用、化简。
输入表达式的文法结构如下：
- 表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
- 项 → [加减 空白项] 因子 | 项 空白项 '*' 空白项 因子
- 因子 → 变量因子 | 常数因子 | 表达式因子｜求导因子
- 变量因子 → 幂函数 | 三角函数 | 自定义函数调用
- 常数因子 → 带符号的整数
- 表达式因子 → '(' 表达式 ')' [空白项 指数]
- 幂函数 → 自变量 [空白项 指数]
- 自变量 → 'x' | 'y' | 'z'
- 三角函数 → 'sin' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数] | 'cos' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数]
- 指数 → '**' 空白项 ['+'] 允许前导零的整数 (注：指数一定不是负数)
- 带符号的整数 → [加减] 允许前导零的整数
- 允许前导零的整数 → ('0'|'1'|'2'|…|'9'){'0'|'1'|'2'|…|'9'}
- 空白项 → {空白字符}
- 空白字符 → （空格） | \t
- 加减 → '+' | '-'
- 求导因子 → 求导算子 空白项 '(' 空白项 表达式 空白项 ')'
- 求导算子 → 'dx' ｜'dy' ｜'dz'
程序架构
类图
以下是我代码中的类，以及类中方法及简要关系示意图：
- Lexer：划分输入字符串
- Parser：解析字符串，构建对象
- Factor：为所有因子提供统一接口，因子中统一不存储指数信息
- ConsFactor：常数因子
- VarFactor：变量因子
- ExprFactor：表达式因子，由 项-系数 对组成
- TriFactor：三角函数因子，由表达式因子和sin标识组成
- DeriveFactor：求导因子，不出现在项中，在Parser中解析后直接存储求导后的表达式因子
- Function：自定义函数，不出现在项中，在Parser中解析后直接存储代入变量后的表达式因子
- Term：项。解析时，因子统一存到 factors:ArrayList中，输出时再化简。
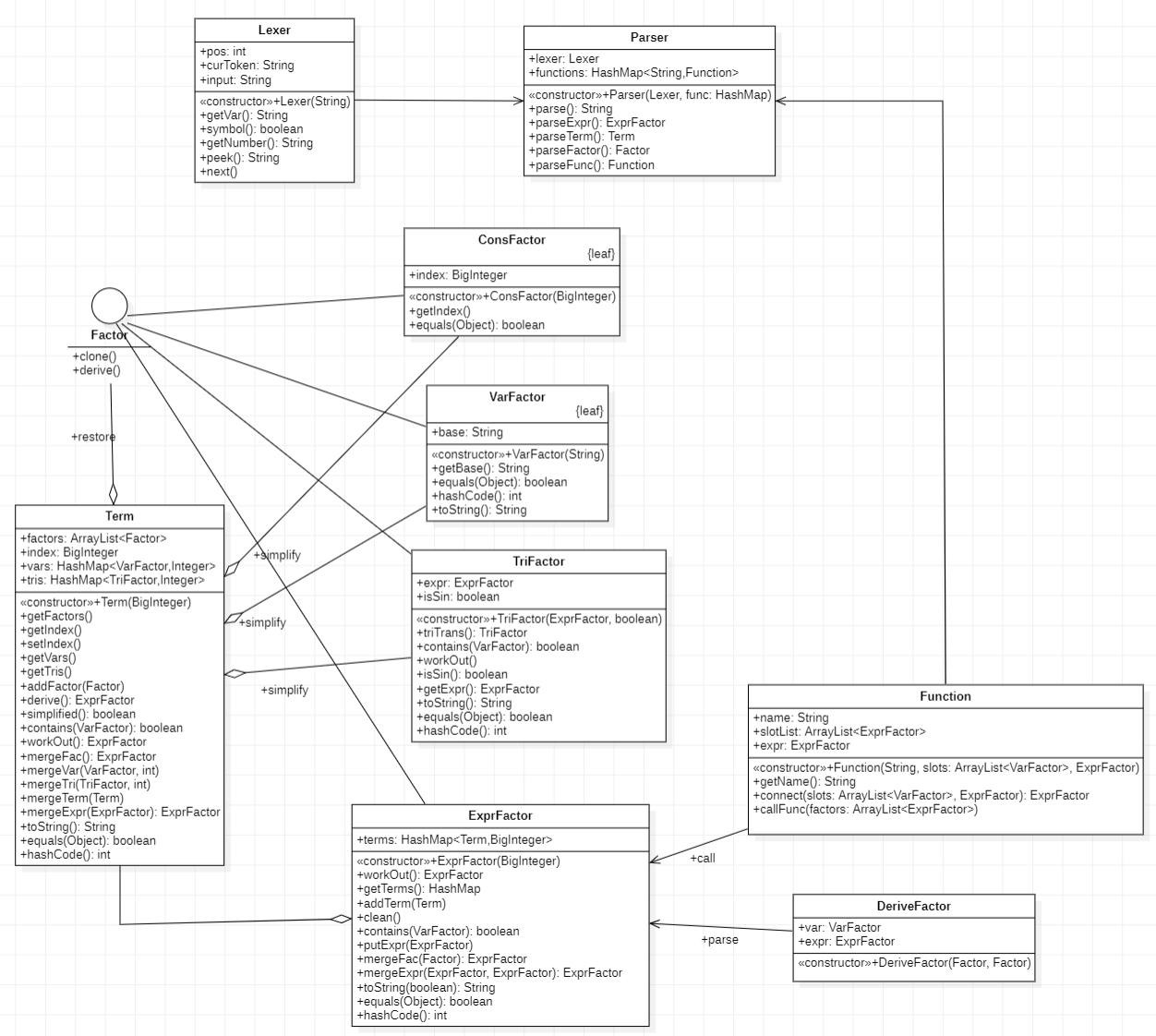
Term类
解析后的Term中，只有factors可以非空，即先存储后化简。好处：
- 方便代入自定义函数。自定义函数返回表达式，统一存在factors中能解决各因子类兼容问题。
Term最后输出的形式可以表达为：
$$term = index \times x^a \times y^b \times z^c \times \Pi sin(...)^p \times \Pi cos(...)^q $$
因此Term类设置了index、vars、tris槽，化简时按照因子类型归类。其中，vars和tris使用的时 因子-指数 对的形式存储，各因子都重写了 equals() 和 hashCode() 方法，方便合并同类项。
因子类
各因子同时实现深拷贝和求导方法。
- 深拷贝：因子的叶类为常数类和变量类。实现了叶类的拷贝，其他因子按结构递归拷贝。
- 求导：在项化简合并前求导，此时因子都存在factors槽中。项求导的基本方法是以因子为单位，使用链式法则求导。各因子求导返回表达式因子。
Function类
Function的存储和调用中，实现使用了占位符slot。定义时，解析好的字符串通过 connect() 方法，将对应位的因子替换为 slot 存储。调用时给 slot 赋值，返回表达式的深拷贝。（实现详解见重构部分）
类度量
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| expression.DeriveFactor | 1.0 | 1.0 | 4.0 |
| expression.ConsFactor | 1.2 | 2.0 | 6.0 |
| expression.VarFactor | 1.2857142857142858 | 2.0 | 9.0 |
| MainClass | 2.0 | 2.0 | 2.0 |
| expression.TriFactor | 2.0 | 8.0 | 22.0 |
| expression.ExprFactor | 2.7142857142857144 | 9.0 | 38.0 |
| expression.Function | 2.75 | 6.0 | 11.0 |
| Lexer | 2.8333333333333335 | 7.0 | 17.0 |
| Parser | 3.125 | 7.0 | 25.0 |
| expression.Term | 3.1904761904761907 | 10.0 | **67.0 ** |
| Total | 201.0 | ||
| Average | 2.4814814814814814 | 5.4 | 20.1 |
方法度量
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| expression.ConsFactor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ConsFactor.ConsFactor(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ConsFactor.derive(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ConsFactor.equals(Object) | 1.0 | 2.0 | 1.0 | 2.0 |
| expression.ConsFactor.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.DeriveFactor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.DeriveFactor.derive() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.DeriveFactor.derive(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.DeriveFactor.DeriveFactor(Factor, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ExprFactor.addTerm(Term) | 7.0 | 3.0 | 5.0 | 6.0 |
| expression.ExprFactor.clean() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ExprFactor.clone() | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.contains(VarFactor) | 3.0 | 3.0 | 2.0 | 3.0 |
| expression.ExprFactor.derive(Factor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.equals(Object) | 1.0 | 2.0 | 1.0 | 2.0 |
| expression.ExprFactor.ExprFactor(BigInteger) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.ExprFactor.hashCode() | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.mergeExpr(ExprFactor, ExprFactor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.mergeFac(Factor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.putExpr(ExprFactor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.ExprFactor.toString(boolean) | 17.0 | 3.0 | 9.0 | 9.0 |
| expression.ExprFactor.workOut() | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.Function.callFunc(ArrayList) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.Function.connect(ArrayList, ExprFactor) | 11.0 | 1.0 | 6.0 | 6.0 |
| expression.Function.Function(String, ArrayList, ExprFactor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.Function.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.addFactor(Factor) | 4.0 | 1.0 | 4.0 | 4.0 |
| expression.Term.clone() | 3.0 | 1.0 | 4.0 | 4.0 |
| expression.Term.contains(VarFactor) | 10.0 | 5.0 | 5.0 | 8.0 |
| expression.Term.derive(Factor) | 8.0 | 3.0 | 4.0 | 5.0 |
| expression.Term.equals(Object) | 6.0 | 6.0 | 2.0 | 7.0 |
| expression.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.getTris() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.getVars() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.mergeExpr(ExprFactor) | 5.0 | 1.0 | 3.0 | 3.0 |
| expression.Term.mergeFac(Factor) | 5.0 | 2.0 | 4.0 | 5.0 |
| expression.Term.mergeTerm(Term) | 2.0 | 1.0 | 3.0 | 3.0 |
| expression.Term.mergeTri(TriFactor, int) | 8.0 | 3.0 | 4.0 | 6.0 |
| expression.Term.mergeVar(VarFactor, int) | 5.0 | 2.0 | 3.0 | 4.0 |
| expression.Term.reverse() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.setIndex(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.simplified() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.Term(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.Term.toString(boolean) | 17.0 | 5.0 | 10.0 | 12.0 |
| expression.Term.workOut() | 2.0 | 2.0 | 3.0 | 3.0 |
| expression.TriFactor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.contains(VarFactor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.derive(Factor) | 2.0 | 2.0 | 2.0 | 3.0 |
| expression.TriFactor.equals(Object) | 2.0 | 2.0 | 2.0 | 3.0 |
| expression.TriFactor.getExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.isSin() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.toString() | 21.0 | 7.0 | 8.0 | 12.0 |
| expression.TriFactor.TriFactor(ExprFactor, boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.triTrans() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.TriFactor.workOut() | 1.0 | 1.0 | 2.0 | 2.0 |
| expression.VarFactor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.VarFactor.derive(Factor) | 1.0 | 2.0 | 1.0 | 2.0 |
| expression.VarFactor.equals(Object) | 1.0 | 2.0 | 1.0 | 2.0 |
| expression.VarFactor.getBase() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.VarFactor.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.VarFactor.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expression.VarFactor.VarFactor(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getVar() | 3.0 | 2.0 | 4.0 | 4.0 |
| Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.next() | 9.0 | 2.0 | 7.0 | 8.0 |
| Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.symbol() | 4.0 | 1.0 | 3.0 | 4.0 |
| MainClass.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| Parser.expandPower(Term, Factor) | 3.0 | 1.0 | 4.0 | 4.0 |
| Parser.newFactor(String) | 15.0 | 4.0 | 12.0 | 13.0 |
| Parser.parse() | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseExpr() | 4.0 | 1.0 | 4.0 | 4.0 |
| Parser.parseFactor() | 3.0 | 1.0 | 3.0 | 3.0 |
| Parser.parseFunc() | 1.0 | 1.0 | 2.0 | 2.0 |
| Parser.Parser(Lexer, HashMap<String, Function>) | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseTerm() | 6.0 | 1.0 | 4.0 | 4.0 |
| Total | 204.0 | 124.0 | 193.0 | 223.0 |
| Average | 2.5185185185185186 | 1.5308641975308641 | 2.382716049382716 | 2.753086419753086 |
架构迭代过程
项因子的存储和化简
第一次作业中，在 Term.addFactor() 方法中就完成了对各个因子合并化简，而不是在输出时才化简。Term 类中没有设置factors槽，而是存储了唯一的表达式因子，项中由多个表达式因子时，跟已有的表达式因子合并。
- 优点：更快，不需要存储后重新遍历化简，且大指数项不用占用过多内存。
- 缺点：值为 0 的表达式因子很难处理，表达式因子中没有项时难以区分是还没有表达式存入，还是已经通过化简归零。需要设置归零标志位，并在操作时频繁读取标志位。
第二次作业中引入了自定义函数，那么自定义函数的存储中，这种架构就更加不可取了。此时我增加了factors槽，但是还没有放弃优先化简的思想，而是只在函数表达式存储时做了区分：函数存储时存因子到factor中，不化简，调用时立刻化简。为了完成这个结构，又增加了化简标志位。
第三次作业我才完全放弃了先化简的思想。不管是函数还是目标表达式，Term.addFactor()都不进行化简操作，在输出时统一化简，以空间为代价降低了代码的复杂度，简化了类结构，减少了标志位的存储传递。
指数和负号处理
第一次作业中，我按照文法的定义，将指数存储在因子内部。因为Term.addFactor()就对因子合并化简，这种结构就方便 Term类 直接访问和修改指数。
在第一次作业中，我还猜测接下来几周的文法发展方向，可能会实现负变量因子、负三角函数因子的化简，因此支持了所有因子的负数形式。解析是项不存储符号，符号全部由变量存储，即-x*y存储为(-x)*y，-x是一个因子单位。
因此第一次作业中我的Factor类如下：
public interface Factor {
void reverse(); //反转符号
void exp(int num);
}
第二次作业中，因为项延迟化简及需要表达式代入，指数的存储复杂了起来：函数没有指数，x**2需要存储成x*x；-x**3 需要处理成-x x x，需要对已经封装好的因子的符号和指数修改。不仅如此，化简过程中负号更难处理了：Term.mergeFactor()对递归化简因子，在哪一层处理符号需要统一，逻辑上增加了很多麻烦。
第二次作业中我的Factor类如下：
public interface Factor {
void reverse(); //反转符号
boolean getNeg();
void setNeg(boolean neg);
void exp(int exp);
int getExp();
}
第三次作业重构后，parser在Term层读取因子指数和符号，即：
public Term parseTerm(){
...
do {
if (lexer.peek().equals("*")) {
...
}
Factor factor = parseFactor();
if (lexer.peek().equals("**")) {
expandPower(term, factor);
} else {
term.addFactor(factor);
}
} while (lexer.peek().equals("*"));
...
}
因子类不再管理负号和指数，由项在化简时通过HashMap管理，降低了因子类的复杂度。
因子判等
在第二次作业后重写了equals()和hashCode()方法，支持了项HashMap管理因子和表达式HashMap管理项。
实际上重写的只有叶类ConsFactor和VarFactor，其他类递归调用判等。
深克隆
第一、二次作业中，因为对克隆的不了解，我在Term类中，继承了Serializable类，使用序列化和反序列化实现深克隆。
第三次作业中，参考训练的代码，对叶函数克隆，其他类递归克隆，实现了更优美的克隆方案。
函数调用
第二次作业中，函数的slot实现，我通过建立三个ExprFactor引用，在构建函数时，如果传入对应变量，就在函数存储的表达式中存入对应引用。在调用时，只需修改三个引用的值，返回的表达式拷贝就是我们需要的表达式。
但在第三次作业中，我以更符合逻辑的方法，保存了引用栈：
private<ArrayList<ArraList<ExprFactor>>> slotList;
外层是自变量序列，内层时每一个自变量对应位置的引用序列，调用时两层遍历，依次给各个引用赋值。
后来在bug修复期间，觉得这种实现没有必要，没有第二次作业中的架构优雅，又改了回来：
private ArrayList<ExprFactor> slotList;
bug修复
我在bug修复期间也使用了自动化工具生成数据，但我发现效果不如自己手搓数据好。手搓数据能够更好的覆盖各个数据类型，能更好的测试0，1等极端数据。
我的bug：
- 负号处理：表达式乘负数负号处理不到位
- 表达式判零：第一次作业中，先化简，判零标志位没设置好
- 多个0表达式叠加：未注意HashMap覆盖
心得体会
第一次接触oo，我在摸爬滚打中慢慢优化自己的代码结构，几乎每次作业都要重构一般的代码，但也慢慢让结构变得更合理，操作更简单，实现方式更加优雅。第一次第二次作业不能保证强测全对，第三次已经没有错误的测试点了（虽然没逃过互测），看到自己的进步我也很高兴。
但是在互测中我构造的测试数据还是比较弱，相比同房同学找到的bug很少。希望接下来在空闲时间多研究数据的生成，对自己和别人的程序都能有更好的理解。
...全文
请发表友善的回复…
发表回复
SoftwareTeacher 8天前
- 打赏
- 举报
第一次接触oo，我在摸爬滚打中慢慢优化自己的代码结构，几乎每次作业都要重构一般的代码，但也慢慢让结构变得更合理，操作更简单，实现方式更加优雅。第一次第二次作业不能保证强测全对，第三次已经没有错误的测试点了（虽然没逃过互测），看到自己的进步我也很高兴。
赞，不断进步！