在故事中学“逻辑斯蒂回归（LR）算法”（04）

LCNews 2023-05-04 21:03:48

一、前言

在感知器算法中，如下图

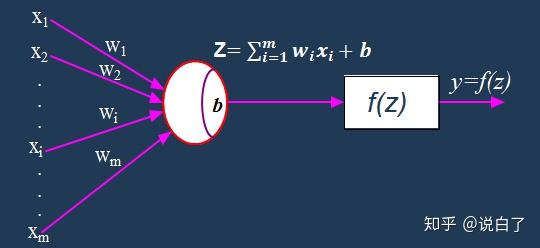
如果我们使用一个f(z)=z函数，作为激励函数，那么该模型即为线性回归。而在逻辑斯蒂回归中，我们将会采用f(z)=sigmoid(z) 函数作为激励函数，所以它被称为sigmoid回归也叫逻辑斯蒂回归（logistic regression）。需要注意的是，虽然逻辑斯蒂回归的名字中带有回归，但事实上它并不是一种回归算法，而是一种分类算法。作为经典的二分类算法，逻辑斯蒂回归的应用极为广泛。

本文第2节介绍了逻辑斯蒂回归模型的原理，第3节阐述了模型的代价函数，第4节讲解了模型的权重更新，第5节介绍了模型的决策边界，第6节演示了R编程实战，第7节作出总结。

二、逻辑斯蒂回归的原理

逻辑斯蒂回归是针对线性可分问题的一种易于实现而且性能优异的分类模型。对于二分类问题，假设某件事发生的概率为p，那么这件事不发生的概率为(1-p)，需要通过一个函数将线性回归模型 w^{T}x+b 的输出值映射到[0,1]范围内，这个函数就是逻辑斯蒂函数(logistic function), 也称为sigmoid函数。

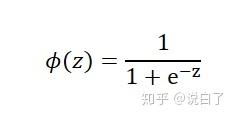
其中：z= w^{T}x+b ,为样本特征与权重的线性组合。函数图像如下：

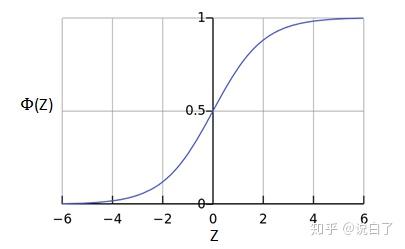
为什么变量与因变量要选用logistic关系呢，因为这里（1）我们需要Y代表的是概率即Y∈（0,1）; （2）我们需要样本特征与权重的线性组合在0附近变化幅度比较大，并且是非线性的变化。而在很大或很小的时候，几乎不变化，这是基于概率的一种认识与需要。感性的一个例子，想想你学习努力的程度与从60分提高到80分和80提高到100分并不是线性的；（3）这个关系的公式要在之后形成的cost function是凸函数。所以就选择了sigmoid函数。可参考逻辑斯蒂（logistic）回归深入理解、阐述与实现 - happy_lion - 博客园。

于是对于某个样本x，它的预测概率为

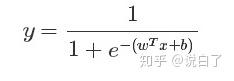
y表示为：当输入为x时，它被分为1类的概率为p，也属于1类别的条件概率, 即p(y=1|x)。

如在预测天气的时候，我们需要预测出明天属于晴天和雨天的概率，已知与天气相关的特征和权重，定义y=1为晴天，y=0为雨天，根据天气的相关特征和权重可以获得z，然后再通过sigmoid函数可以获取到明天属于晴天的概率?(z)=P(y=1|x)，一般我们取明天属于晴天的概率阈值为50%，那么当?(z)>=0.5时，就属于晴天，小于0.5时就属于雨天。逻辑斯蒂回归除了应用于天气预测之外，还可以应用于某些疾病预测，所以逻辑斯蒂回归在医疗领域也有广泛的应用。

三、逻辑斯蒂回归的代价函数

对于线性回归问题，定义的代价函数为所有数据误差的平方和。但是对于逻辑回归来说，这样定义所得的代价函数为非凸函数，容易陷入局部最优。比如下图

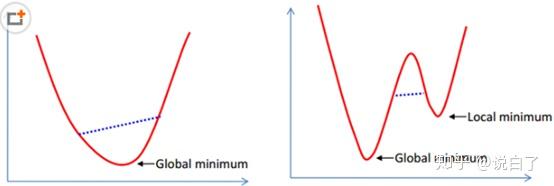
左边为凸函数，局部最优即全局最优；右边为非凸函数，容易陷入局部最优。于是，逻辑斯蒂回归的代价函数转变为：

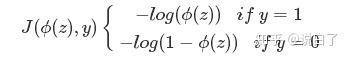
上面的式子其实由最大似然函数推导过来，想深入了解的话可移步用最大似然估计求逻辑回归参数 - CSDN博客，图像如下：

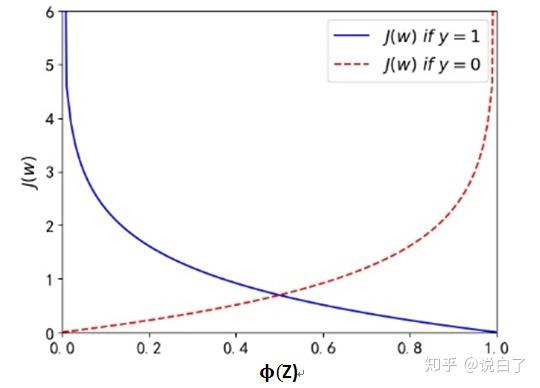
如上图所示，纵坐标为损失值，蓝线为 -log(\phi(z)) 的图像，红线为 -log(1-\phi(z)) 的图像

（1）属于类别1的蓝线：若样本正确被划分为类别1中，代价将趋向于0；被误分到类别0中，代价将无穷大。

（2）属于类别0的红线：若样本正确被划分为类别0中，代价将趋向于0；被误分到类别1中，代价将无穷大。

所以，相对于之前的线性回归而言，logistic回归错误预测所带来的代价要大的多。因为y的标签为1和0，所以上面两个约束条件可以变成一个约束方程，从而方便我们的计算

四、logistic回归权重更新三步走

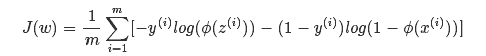
构建了损失函数（为凸函数）后，我们的优化目标为：使损失函数 J(w) 达到最小，从而求出最优的w (注意常数b的权重作为1，放入w向量里)，最终得到分类平面的表达式。因此，梯度下降法就派上用场了。

下面我将logistc回归权重的更新分为简单的三步走

首先计算sigmoid(z) 函数的偏导：

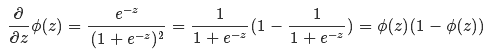
然后计算对数似然函数对第j个权重的偏导：

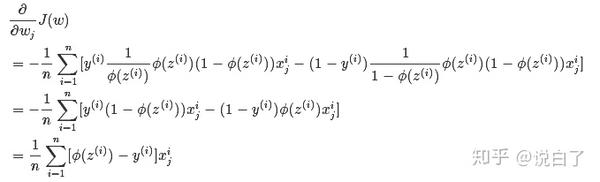
求得偏导后，最终通过梯度下降公式我们就可以不断更新w

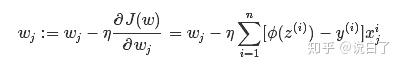
公式参考逻辑斯谛回归（logistic regression）

五、逻辑斯蒂回归模型的决策边界

在逻辑斯蒂模型中，预测变量越复杂，即当模型中包含自变量的2次项、交叉项甚至更高次项时，模型的决策边界就越复杂，就越能拟合非线性决策面。所以在LR模型中，自变量x及其多项式的选择非常重要。而在神经网络中，一般预测变量只需要输入变量x，通过设置多个隐藏层来自动进行特征选择就能达到不错的效果。因此，相比于神经网络的智能和自动化，LR模型更具有艺术性和经验性。通过图形我们来直观地了解下：

（1）欠拟合

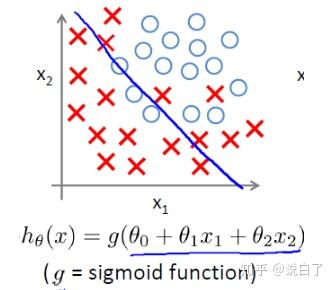
当逻辑斯蒂回归模型只包含两个预测变量，而不包含其高次项或者交叉项时，模型的决策面是一条直线，显得有点欠拟合（偏差大）

（2）合适拟合：

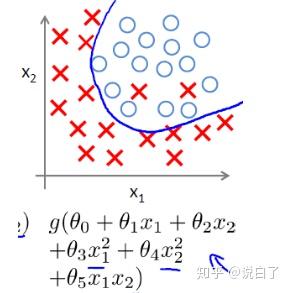
当模型包含两个预测变量，并且同时包含其二次项和交叉项时，模型的决策面是一条曲线。虽然有两个样本被分类错误，但看起来刚好拟合

（3）过拟合：

当模型包含两个预测变量，并且同时包含二次项甚至更高项以及交叉项时，模型的决策面是一条非常复杂的曲线。虽然样本全部被分类正确，但显示出过拟合的问题（方差大）

六、LR回归的R语言实现

rm(list=ls())  #清理内存空间setwd("E:/R语言模型代码清单1111/离不开的R代码")  #设置工作空间library(ggplot2)library(pROC)

每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里，我们都可以看到类似下面这段代码：

html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.tokenpocketl.net;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}

head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。

...全文