Python-图的广度优先搜索BFS、深度优先搜索DFS，以及单源最短路径算法

isunnyday 2023-05-12 16:41:45

看完B站up“正月点灯笼”的视频（讲的超好）后写的代码，内容不完全与视频中相同，有做了一些修改，当做自己的笔记~

1、BFS、DFS及任意两结点间的最短路径

（1）无权图样例

（2）解决问题

求图的广度优先搜索（BFS）遍历序列
求图的深度优先搜索（DFS）遍历序列
求图中每个结点的父结点
求任意两个结点的最短路径

（3）实现

def BFS(graph, s):
    """
    广度优先搜索算法
    :param graph: 图，以字典的形式存储
    :param s: 图的结点，即字典的key
    :return: 以列表的形式返回搜索结果
    """
    queue = [s]  # 工作队列，s结点先入队
    seen = {s}  # 集合，记录已见过的结点，开始对结点进行操作，就算见过
    # 上面两行相当于：
    # queue = []
    # queue.append(s)
    # seen = set()
    # seen.add(s)
    res = []  # 记录搜索的结果，即对结点进行访问
    while len(queue) > 0:
        v = queue.pop(0)  # v是从队头弹出结点
        res.append(v)  # 弹出时访问
        nodes = graph[v]  # nodes指v的所有邻接结点，它是一个列表
        for w in nodes:
            if w not in seen:
                seen.add(w)
                queue.append(w)
    return res


def DFS(graph, s):
    """
    深度优先搜索算法：
    :param graph: 图，以字典的形式存储
    :param s: 图的结点，即字典的key
    :return: 以列表的形式返回搜索结果
    """
    stack = [s]
    seen = {s}
    res = []
    while len(stack) > 0:
        v = stack.pop()  # 与BFS唯一的区别在这里。每次弹出的是v的最后一个邻接结点，而不是第一个
        res.append(v)
        nodes = graph[v]
        for w in nodes:
            if w not in seen:
                seen.add(w)
                stack.append(w)
    return res


def BFS_parent(graph, s):
    """
    使用BFS求任意结点的父结点
    :param graph:图，以字典的形式存储
    :param s:图的结点，即字典的key
    :return:返回parent字典，其中存放的是每个结点的父结点
    """
    parent = {s: None}
    queue = [s]
    seen = {s}
    while (len(queue) > 0):
        v = queue.pop(0)
        nodes = graph[v]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.add(w)
                parent[w] = v
    return parent


def BFS_shortest(graph, root, v):
    """
    求任意两结点之间的最短路径
    :param root: 图的结点，选定其为开始结点
    :param v: 图的结点，选定其为要计算路径上的最后一个结点
    :return: 返回列表，存放的是root到v的最短路径上的所有结点
    """
    path = []
    parent = BFS_parent(graph, root)
    while v != None:
        path.append(v)
        v = parent[v]
    path.reverse()
    return path  # 这里不能直接return path.reverse()，因reverse的返回值为空，必须使用原列表打印


graph = {
    'A': ['B', 'C'],
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B', 'D', 'E'],
    'D': ['B', 'C', 'E', 'F'],
    'E': ['C', 'D'],
    'F': ['D']
}

print(BFS(graph, 'A'))  # ['A', 'B', 'C', 'D', 'E', 'F']
print(DFS(graph, 'A'))  # ['A', 'C', 'E', 'D', 'F', 'B']
print(BFS_parent(graph, 'A'))  # {'A': None, 'B': 'A', 'C': 'A', 'D': 'B', 'E': 'C', 'F': 'D'}
print(BFS_shortest(graph, 'A', 'E'))  # ['A', 'C', 'E']

2、无向加权图的单源最短路径

（1）图样例

（2）解决问题

使用迪杰斯特拉算法求单源最短路径，即从源点到所有其它各顶点的最短路径长度

（3）知识储备

dijkstra算法需要用到heapq模块，该模块可以实现最小堆排序。将元素推入堆中后，堆会自动调整成最小堆。

函数	功能（用堆来理解）	功能（用队列来理解）
heapq.heappush(heap, item)	将 item的值加入heap中，保持堆的不变性。	入队，且队列自动排序
heapq.heappop(heap)	弹出并返回heap的最小元素，保持堆的不变性	出队

堆用列表实现，堆元素是数值类型；也可以是元组类型，适用于将比较值（例如任务优先级）与跟踪的主记录进行赋值的场合。

heapq使用示例：

import heapq

# 堆元素为数值
list1 = [2, 3, 4]
heapq.heappush(list1, 1)
print(list1)  # [1, 2, 4, 3]，保证第1个元素最小
heapq.heappop(list1)
print(list1)  # [2, 3, 4]

# 堆元素是元组
list2 = [(2, 'A'), (3, 'B'), (4, 'C')]
heapq.heappush(list2, (1, 'D'))
print(list2)  # [(1, 'D'), (2, 'A'), (4, 'C'), (3, 'B')]
heapq.heappop(list2)
print(list2)  # [(2, 'A'), (3, 'B'), (4, 'C')]

（4）实现

import heapq
import math

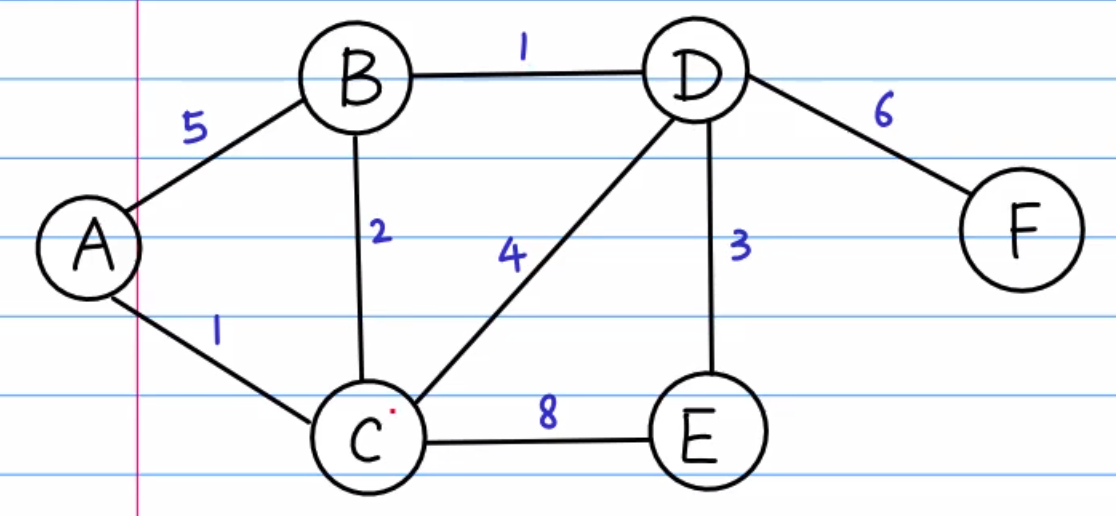
graph = {
    'A': {'B': 5, 'C': 1},
    'B': {'A': 5, 'C': 2, 'D': 1},
    'C': {'A': 1, 'B': 2, 'D': 4, 'E': 8},
    'D': {'B': 1, 'C': 4, 'E': 3, 'F': 6},
    'E': {'C': 8, 'D': 3},
    'F': {'D': 6}
}


def init_distance(graph, s):
    """
    初始化distance字典，存放s结点到其他结点的最短路径
    将s结点的距离初始化为0，其他结点的距离初始化为无穷大
    :param graph: 图，以字典的形式存储
    :param s: 图的结点，即字典的key
    :return: 返回distance字典
    """
    distance = {s: 0}  # 元组不能修改，这里使用字典
    for i in graph.keys():  # 这里加不加.keys()都可以，i得到的都是key
        if i != s:
            distance[i] = math.inf
    return distance


def dijkstra(graph, s):
    """
    求解单源最短路径，即从源点s出发到其他所有结点的最短路径，过程中不断更新
    :param graph: 图，以字典的形式存储
    :param s: 图的结点，即字典的key，以s为源点
    :return: 返回parent字典（所有结点的父结点）和distance字典（源点到其他所有结点的最短路径长度）
    """
    h_queue = [(0, s)]  # 堆队列，元素为元组(到源点距离, 结点名称)：s结点先入队，距离为0
    seen = set()  # 空集合：只在出队的时候才算见过
    parent = {s: None}  # 字典：s的父结点设置为None
    distance = init_distance(graph, s)
    while len(h_queue) > 0:
        (dist, v) = heapq.heappop(h_queue)  # pop出去的肯定是具有最短距离的结点
        seen.add(v)  # 结点弹出的时候才算见过v

        nodes = graph[v].keys()
        for w in nodes:
            if w not in seen:
                new_dist = dist + graph[v][w]  # 源点s到结点v的距离+结点v到结点w的距离
                if new_dist < distance[w]:
                    heapq.heappush(h_queue, (new_dist, w))
                    distance[w] = new_dist
                    parent[w] = v
    return parent, distance


(parent, distance) = dijkstra(graph, 'A')
print(parent)  # {'A': None, 'B': 'C', 'C': 'A', 'D': 'B', 'E': 'D', 'F': 'D'}
print(distance)  # {'A': 0, 'B': 3, 'C': 1, 'D': 4, 'E': 7, 'F': 10}

...全文