论文解读：解救深度学习过拟合的神器——非线性系数

DMenYin 2023-06-11 15:48:24

导语

设计出高性能的神经网络架构是AI从业者追求的目标，但是并没有通用的设计准则。在不久前发表的一篇论文中，研究者提出一种指标——非线性系数，可以很好地度量深度神经网络的过拟合程度。下面是对这篇论文的解读。

论文题目：The Nonlinearity Coefficient - Predicting Overfitting in Deep Neural Networks论文地址：https://arxiv.org/abs/1806.00179

如何判断神经网络的性能

在神经网络在各个领域不断攻城略地的今天，如何设计一个性能优良的网络，和判断网络是否能够能够被训练，成为了科学家和工程师们的主要问题。针对这个问题，本文介绍了一种叫做非线性系数（NLC）的度量方式，NLC是针对梯度爆炸和塌陷域的一种度量方法。

通过NLC，可以对一个神经网络的单个梯度计算所获得的信息量做出一个较为精确的估计。同时论文中通过大量实证研究，说明了NLC能够较好的预测全连接网络的测试误差，这使得通过计算 NLC ，在一定程度上指导神经网络的设计。

此外，本文还发现了避免过度偏激的神经元激活的必要性，以及残差连接对于降低NLC值和提高网络性能的重要性。在文章的第五部分，文章还介绍了NLC 与网络中非线性化程度之间的一个有趣的关系，该关系可以用线性函数近似。

文章的最后一部分，作者讨论了NLC的鲁棒性，并且认为NLC是目前最好的通用网络性能预测器，同时对过拟合有较好预测效果。

本文的工作在《The exploding gradient problem demystified - definition, prevalence, impact, origin, tradeoffs, and solutions.》基础上展开，下面将这篇文章表示为[1]，该文章提出了一个叫做梯度规模系数(GSC)的度量方式。GSC是第一个关于梯度爆炸是否会产生的度量方式。提出了塌陷域(collapsing domain problem)问题，该问题是指在特定区域内，随着深度的增长，更深处隐藏层的激活函数对不同的数据点的响应越来越相似。对NLC感兴趣的读者可以通过阅读文章[1]获得更多相关内容。

数学预警

为了明确且无歧义的介绍NLC的定义以及介绍方式，接下来两部分将先介绍本文使用的一些术语与数学标记，然后介绍NLC的数学定义。如果你对数学不感兴趣，可以略过以下两部分内容。

数学准备——术语与标记

NLC的数学本体

实证研究

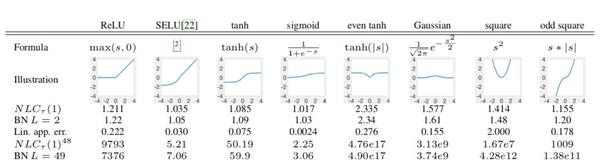
本文通过实验验证了 NLC 在实践中能够捕获梯度信息量。随机生成了大量的神经网络结构。在生成过程中，改变了网络的深度，初始权重的大小，初始偏差的大小，非线性函数，归一化的方法，残差连接的存在，跳过连接的位置和跳过连接的强度。

实验从8个非线性的集合(表2)中随机挑选非线性函数，然后随机扩张、横向偏移和降低偏差。注意，这里只考虑了全连接的前馈网络，因为在深层网络的分析研究中这是比较通用的例子。生成上述网络后，接下来研究它们在以下三个数据集上的表现:

MNIST
CIFAR10
waveform-noise

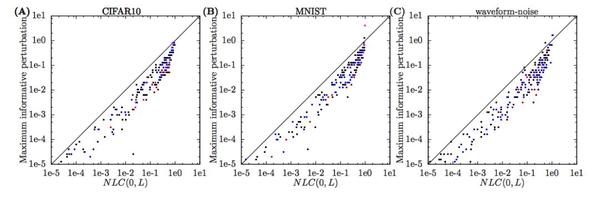
实验为每个数据集抽样了250个架构，并计算了NLC (0,l)以及输入空间中区域相对大小的中位数，在输入空间中，局部线性逼近以随机方向提供信息。结果见图1。实际上，这两个量之间存在着密切的关系。

然后用 SGD 训练这750个神经网络。对每个架构进行了的独立网格搜索，以确定最佳的步长，从而消除这个潜在的混淆。这导致了总共超过15,000次全面训练。文[1]证明了为每个架构独立设置步长的重要性。文章[1]证明了为每个架构独立设置步长的重要性。

模型设计准则

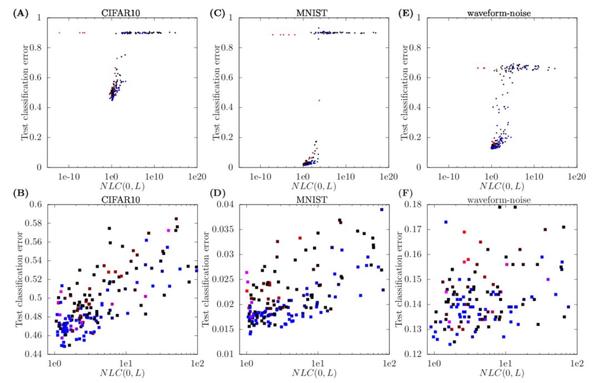
在图2中，纵轴为测试误差，横轴为NLC(0,L)，每个点是一个神经网络。作者发现，对于三个数据集，测试错误都与 NLC 高度相关。事实上，对于NLC的值在1~100之间(图 b / d / f)的网络来说，测试错误似乎被限制在 NLC 的线性函数之下。

对于所有三个数据集，只有当 NLC 在一个很窄的范围内，大约在1到2之间时，才能获得最佳性能。作者还发现，大多数随机结构都有一个大于最优值的 NLC。换句话说，这些网络非常容易过拟合。因此，本文给出了神经结构设计的第一条准则：

通过观察NCL的值，来选择拥有适当复杂度的神经网络

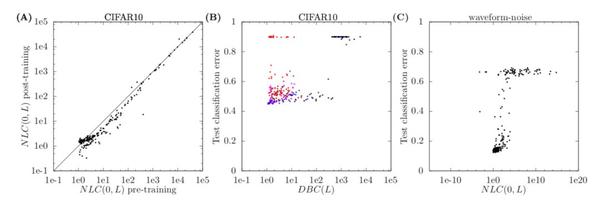
请注意，NLC 很容易计算。在图 3A 中，对比在CIFAR10数据集上，训练前后的 NLC 值。在绝大多数情况下，变化很小。在图2 a / c / e 中，我们注意到，在左上角有一些异常点，它们代表了不可训练的架构。

文章对图2中的点进行了颜色编码，其中 a 点越红，DBC(l) 越高。实验发现上述异常值与表现出最高偏差的网络结构相对应。为了进一步研究这种效应，作者修改了在 CIFAR10 上训练的神经网络的结构，使它们可能产生更高的域偏置值。

对这些网络进行训练后，将 DBC(l) 与对应的测试错误呈现在图3B中。虽然偏差在一定程度上似乎不会影响性能，但是所有的DBC 超过300的网络都表现出随机性。因此，根据上述结果，给出了神经结构设计的第二条准则：

通过观察DBC(L)的值，来避免太高的偏差。

文[1]详细说明了 k 稀释效应(e k-dilution effect)，这种效应导致在在反向传播过程，残差连接大幅度减少 GSC 的增长。此外，他们还证明，ResNets 大约实现了一个正交的初始状态，并且认为不仅减少了复杂度，而且提高了性能。

在图2中，对点进行彩色处理，使得架构的残差连接越强，点就越蓝。没有残差连接的架构没有蓝色。正如预期的那样，本文发现带有残差连接的架构表现出较低的 NLC。因此，制定了第三条准则：

利用残差连接来降低 NCL，提升网络准确性。

NLC对非线性单元的解释

这似乎意味着，改变非线性的线性近似，NLC 会随之改变。对于所有CIFAR10上训练，NLC(0，l)大于10的网络，用0.1(s) + 0.9s 代替了非线性激活函数（即用线性函数大量稀释了非线性）。

对这些架构进行了训练，在110个案例中有102个案例得到了改进。这表明比起非线性的精确形状，NLC 对网络性能的度量更加重要。

总结

本文介绍了非线性系数，对全连接网络来说，这是一个强大的预测器，与网络梯度的信息性和个体非线性的线性近似性密切相关。因此，NLC 代表了一个简单而有力的假设，即网络的复杂性及过拟合的可能性。

非线性系数方法（NLC）的计算成本低廉，整个训练过程稳定，具有重要的实用价值。通过一项大规模的实证研究核实了文章的结果，这项研究还表明，必须避免存在过大的偏差，可以通过残差连接来减少 NLC，并取得进一步的性能收益。

参考文献：

[1]:The exploding gradient problem demystified - definition, prevalence, impact, origin, tradeoffs, and solutions.

作者：彩云小译7号审校：Sylvia 王贝贝

◆ ◆ ◆

每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里，我们都可以看到类似下面这段代码：

html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.czjy.cn;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}

head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。

...全文