高中生也能看懂的“梯度下降”算法（线性回归篇）

2301_77724032 2023-07-14 21:54:39

## 文章背景：

最近在研究机器学习的相关算法，查阅很多专业书籍、csdn文章、知乎大神回答、youtube视频，都发现一个高度统一的 “ 问题 ”（严格意义上不能说是问题）：大家在介绍算法的时候，总是喜欢陈列各种复杂的公式、各种见都没见过的符号，虽然这样在“数学上”是严谨的，看起来专业感十足，但不给详细的解释，着实给我这样的小白学习者非常不友好，带来了很多负担。。。（似乎在传达着“这是你应该知道的东西”，于是作为文科生的我，耗尽毕生精力将“谷歌大法”发挥到极致，才对“梯度下降”算法有了一定程度的理解）当我发现“梯度下降”算法也不过如此的时候，我在想：会不会有些人也和我一样是 “ 非科班出身 ”的，还惆怅于数学公式带来的“距离感”，望而生畏？

## 说明：

这篇文章将从文科生小白的视角细细说来，本着让 “ 初中生 ” 也能看懂的精神，力求使用“最直白”、“最简洁”的话术来解释！（可能在数学专业者看来不严谨，但我觉得对读者“亲切”、“友好” 比 “为了严谨而曲高和寡更重要”。）若大神觉得我哪里表达得不到位，欢迎指正~~ (`?ω?′)

## 正文开始：

既然你诚心诚意地想知道 “ 梯度下降 ” 的算法到底是什么样的，相信你应该也了解到了：“线性回归” 是 “梯度下降” 的基础。

那么，我自然是要先给各位童鞋介绍一下：什么是线性回归咯~~

在机器学习的现实应用领域，就是用一条直线来近似地表示“自变量” 和 “因变量” 的关系。

# 第 ① 步

举个例子：

一天，隔壁老王用 1两的面粉，做了 2个大饼。

（这里，面粉的数量是自变量，大饼的数量是因变量，将自变量作为x轴，因变量作为y轴，可以用1 个红点来表示 “面粉——大饼” 的数量关系，如下图）

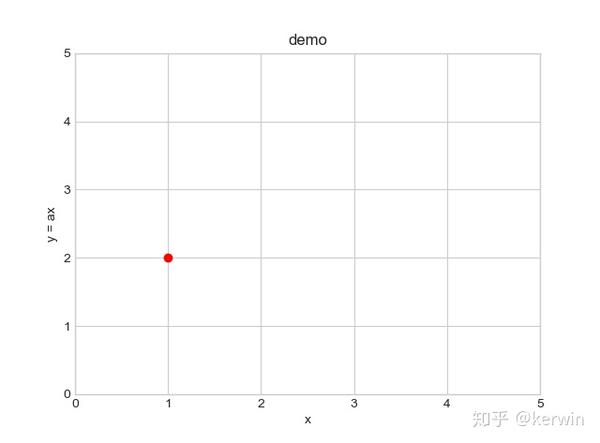
而如果我们尝试着用一条线来描述 “面粉——大饼” 的数量关系，我们自然而然会想到从原点O出发，画一条过红点的线，如下：

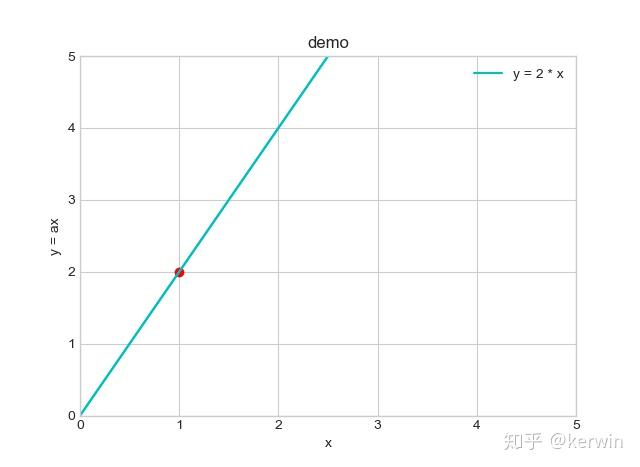
用一条直线来描述现实中收集到的数据——“1两面粉， 2个大饼”

你看，这就是线性回归，简单到令人发指吧？？哈哈哈~

# 第 ② 步

住在我家隔壁的不仅仅有老王，还有小王：

第二天，隔壁小王用 2两的面粉，做了1 个大饼。

此时，我们连线后，有下图：

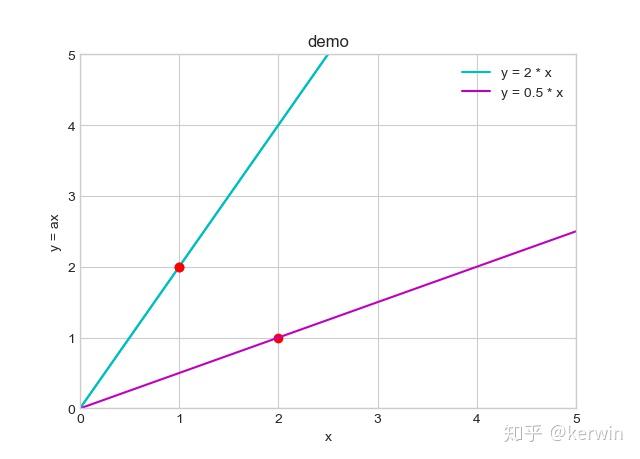
既然画了两条线，那么我们到底取哪条线，才能更恰当地描述 “面粉——大饼” 的数量关系呢？

好像这两条线都不合适吧，似乎中庸一点比较好，那就取它俩中间的线吧~ 如下，我多画了两条线夹在中间：

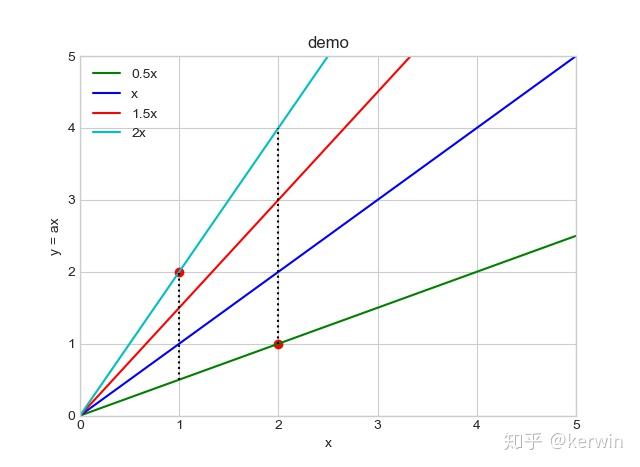
但是，他俩中间理论上可以画出无数条线，那我到底取哪条线最好？

（换句话说，就是我这条线的斜率a到底取多大的值最好？）

# 第 ③ 步

下面开始介绍简单的算法：

我们可以直观地认为，当这条线离那两个红点的距离越近，那么这条线就越能够准确地描述 “面粉——大饼” 的数量关系。而这条线，恰恰也就是我们的目标回归线，我们可以用:

来表示这条未知的目标直线。

a：表示“斜率”  下标{p}：predicted value， 表示“预测值”  下标{a}：actual value， 表示“实际值”（此处一定不要把a和下标{ａ}混淆了）

每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里，我们都可以看到类似下面这段代码：

html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.aimssg.cn;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}

head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。

...全文