从文本分类来看图卷积神经网络

[LCNews]

? “ 图神经网络火了这么久，是时候掌握它了。”

本文包括以下内容，阅读时间10min

• 图神经网络是什么意思
• 文本如何构建图
• 图卷积神经网络
• 源代码实现
• 图卷积神经网络最新进展

本文阅读基础

• 神经网络基础
• 本文不包含拉普拉斯矩阵的数学推导

01“图神经网络”是什么

图神经网络(Graph Neural Network, GNN)是指神经网络在图上应用的模型的统称，图神经网络有五大类别：分别是：图卷积网络（Graph Convolution Networks，GCN）、 图注意力网络（Graph Attention Networks）、图自编码器（ Graph Autoencoders）、图生成网络（ Graph Generative Networks） 和图时空网络（Graph Spatial-temporal Networks）。本文只重点介绍最经典和最有意义的基础模型GCN。

【清华大学孙茂松教授组在 arXiv 发布了论文Graph Neural Networks: A Review of Methods and Applications，作者对现有的 GNN 模型做了详尽且全面的综述】。

02 文本如何构建图

我们要构建一个具有定义好n个节点，m条边的图。

以经典的分类任务为例。我抽屉里有5本不同的机器学习书，里面一共有a个章节，同时所有书里面一共有b种不同的单词(不是单词个数，是所有的单词种类)。然后我们就可以给a个章节和b个单词标记唯一的id，一共n=a+b个节点，这是我们图的节点。

-边的创建-

我们有两种节点，章节和单词。然后边的构建则来源于章节-单词 关系和 单词-单词 关系。对于边章节-单词 来说，边的权重用的是单词在这个章节的TF-IDF算法，可以较好地表示这个单词和这个章节的关系。这个算法比直接用单词频率效果要好[1]。单词-单词 关系的边的权重则依赖于单词的共现关系。我们可以用固定宽度的滑窗对5本书的内容进行平滑，类似于word2vector的训练取样本过程，以此计算两个单词的关系。具体的算法则有PMI算法实现。

point-wise mutual information（PMI）是一个很流行的计算两个单词关系的算法。我们可以用它来计算两个单词节点的权重。节点 i 和节点 j 的权重计算公式如下：

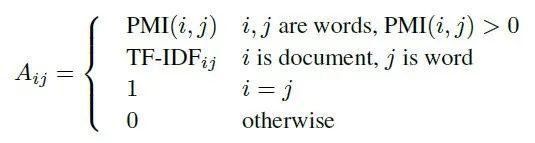
PMI(i, j)的计算方式如下：

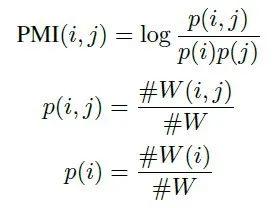
#W(i) 表示所有的滑窗中包含单词节点 i 的个数。

#W(i; j) 表示所有的滑窗中同时包含单词节点 i 和单词节点 j 的个数。

#W 是总的滑窗次数

PMI值为正则说明两个单词语义高度相关，为负则说明相关性不高。因此最后的图构造过程中只保留了具有正值的单词节点对组成的边。

图的节点和边确定了，接下来介绍如何应用图卷积神经网络进行一些学习应用。

【2019年AAAI有一篇论文使用了此方法进行章节分类。题目“Graph Convolutional Networks for Text Classification”】

03 图卷积神经网络

图卷积神经网络(Graph Convolutional Network, GCN)是一类采用图卷积的神经网络，发展到现在已经有基于最简单的图卷积改进的无数版本，在图网络领域的地位正如同卷积操作在图像处理里的地位。

什么是卷积

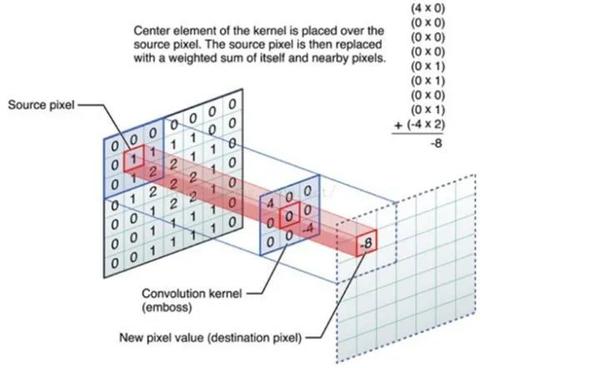
CNN中卷积的本质就是利用共享参数的过滤器 kernel，通过计算中心像素点及相邻像素点的加权和来构成feature map实现空间特征的提取，加权系数就是卷积核的权重系数。卷积核的权重系数通过BP算法得到迭代优化。卷积核的参数正是通过优化才能实现特征提取的作用，GCN的理论很重要一点就是引入可以优化的卷积参数来实现对图结构数据特征的获取。

图卷积的目的类似，寄希望学习到一种节点表示，该节点表示依赖于每个节点及其周边相邻的节点。然后该节点表示就可以输出用作分类任务了，就是我们常说的节点分类。

那么有什么东西来度量节点的邻居节点这个关系呢？拉普拉斯矩阵。举个简单的例子，对于下图中的左图而言，它的度矩阵 ，邻接矩阵 和拉普拉斯矩阵 分别如下图所示，度矩阵（degree matrix） 只有对角线上有值，为对应节点的度，其余为0；邻接矩阵只有在有边连接的两个节点之间为1，其余地方为0；拉普拉斯矩阵 为 。这是比较简单的拉普拉斯矩阵。

以下是重点

图卷积网络(GCN)第一层的传播公式如下：

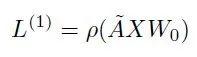
ρ是激活函数，比如ReLU。

上式的\tilde{A} 我们暂时理解等同于邻接矩阵A，代表图的拓扑结构，维度N*N，N表示节点个数;

X是第一层输入的特征矩阵，维度N*M，M表示每个节点的特征向量维度;

Wo是权重参数矩阵，维度M*K，K代表转给下一层的向量维度。

因此第一层输出L1的向量维度就是 N*K。

在上面介绍的文本分类任务中，

X是原始输入，我们用对角线为1的单位矩阵来表示，维度N*N；可以理解为是对节点的one-hot表示。Wo采用的参数是N*K随机初始化(K=200),。

XWo 的维度就是N*200，相当于对每个输入节点做了embedding，维度为200。

A * XWo 这个矩阵乘法怎么理解？这才是理解图卷积的关键。复习一下矩阵乘法公式，发现新生成的L1这个N*K矩阵的每一个节点的K个维度，都是对应该节点的相邻节点邻接权重乘以相邻节点在这个维度上的值的累加和。从而实现了通过一次卷积，GCN可以让每个节点都拥有其邻居节点的信息。

（不准确的讲，图的邻接矩阵乘以图节点embedding，就相当于是做一次卷积)

下面我画了一个示意图

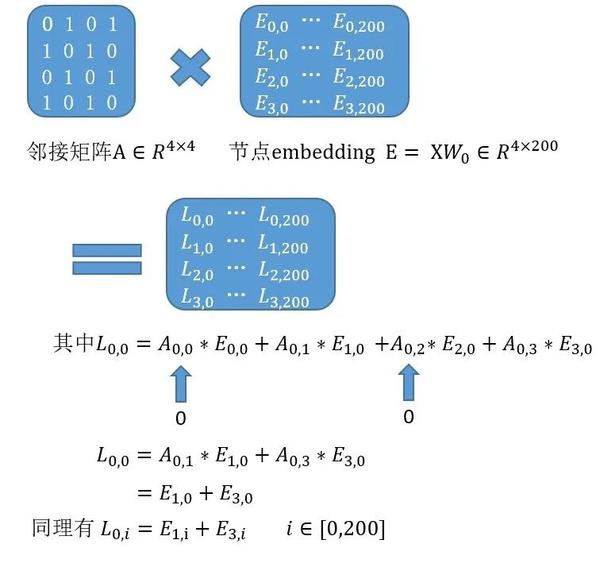
结论：新生成的0号节点的向量全部由相邻的1号节点和3号节点的向量等加权求和得到。从而实现了周边节点卷积(加权求和)得到新的自身的目的。

(邻接矩阵A第一行0 1 0 1表示0号节点和1,3号节点相连，和2号不连接)

如果要让节点拥有周边更广泛的节点信息，可以多次进行卷积。

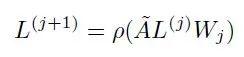
上面的 \tilde{A} 如果用邻接矩阵替代的话有两个缺点。

• 没有考虑节点自身对自己的影响，因为邻接矩阵对角线为0；
• 邻接矩阵没有被规范化，这在提取图特征时可能存在问题，比如邻居节点多的节点倾向于有更大的影响力。

因此更常用的公式是：

又称为规范化对称邻接矩阵(normalized symmetric adjacency matrix)。关于这个公式理解，可以参考[1]

04 pytorch代码实现

class gcn(nn.Module):    def __init__(self, X_size, A_hat, args, bias=True): # X_size = num features        super(gcn, self).__init__()        self.A_hat = torch.tensor(A_hat, requires_grad=False).float()        self.weight = nn.parameter.Parameter(torch.FloatTensor(X_size, args.hidden_size_1))        var = 2./(self.weight.size(1)+self.weight.size(0))        self.weight.data.normal_(0,var)        self.weight2 = nn.parameter.Parameter(torch.FloatTensor(args.hidden_size_1, args.hidden_size_2))        var2 = 2./(self.weight2.size(1)+self.weight2.size(0))        self.weight2.data.normal_(0,var2)        if bias:            self.bias = nn.parameter.Parameter(torch.FloatTensor(args.hidden_size_1))            self.bias.data.normal_(0,var)            self.bias2 = nn.parameter.Parameter(torch.FloatTensor(args.hidden_size_2))            self.bias2.data.normal_(0,var2)        else:            self.register_parameter("bias", None)        self.fc1 = nn.Linear(args.hidden_size_2, args.num_classes)    def forward(self, X): ### 2-layer GCN architecture        X = torch.mm(X, self.weight)        if self.bias is not None:            X = (X + self.bias)        X = F.relu(torch.mm(self.A_hat, X))        X = torch.mm(X, self.weight2)        if self.bias2 is not None:            X = (X + self.bias2)        X = F.relu(torch.mm(self.A_hat, X))        return self.fc1(X)# 第一层权重维度 args.hidden_size_1取200，# 第二层权重维度args.hidden_size_2取20；# args.num_classes=5

---

每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里， 我们都可以看到类似下面这段代码：

html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.aimssg.cn;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}

head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。