2023软工K班结对编程任务

[吴鑫雄102101518]

https://github.com/FZUTeriri/Nomorebets
https://www.bilibili.com/video/BV1Sh4y167yB

一、结对探索

1.1 队伍基本信息

结对编号：12；队伍名称：发际线和我作队；

学号	姓名	作业博客链接	具体分工
112101129	陈佳俊	https://bbs.csdn.net/topics/617401360	前后端全栈开发，AI算法模型
102101518	吴鑫雄	https://bbs.csdn.net/topics/617401369	原型设计，AI算法，单元测试，视频制作

1.2 描述结对过程

1.3 非摆拍的两人在讨论设计或结对编程过程的照片

二、原型设计

2.1 原型工具的选择

• 我们原型设计选择了墨刀，为什么选择墨刀呢？因为它简单好用易上手，功能还十分强大。

选择的过程：

• 之前看了结对编程作业博客的要求还以为只能用那上面列举的工具，然后我们就使用了摹客，还下了个本地app，但是在用过之后发现用不来，效果也不好而且界面也不够美观，然后就又去看了眼要求，发现列举完的工具后面有个“等”（震惊...）。之后去尝试了学长推荐的墨刀，没有比较就没有伤害，确实好用，而且界面更加美观易懂里面的组件也很多，加上b站和csdn上面也有挺多墨刀的教学，所以我们选择了墨刀。

2.2 遇到的困难与解决办法

• 原型设计过程中最大的困难就是怎么设计出强交互性的原型，我们最初的想法就是想要把整个游戏过程包括掷骰，选骰，选倍率，得分等等一系列的交互做出来，然后发现这不现实，因为这工作量确实有点大，然后我们借鉴参考了下其他人和往年学长学姐的原型作品，我们领悟到了什么是原型，原型就要有原型的样子，不要想那些花里胡哨的东西。最终对原型进行简化。我们最大的收获就是搞清楚了原型的作用和意义以及设计思路，原型让程序员在编程的时候就只需要考虑功能的实现而无需考虑界面布局和交互跳转的逻辑，让程序员能更专心地投入到功能代码的编写。（反正前端我照着原型贴）

2.3 原型作品链接

原型作品链接

2.4 原型界面图片展示

1.这是我们的欢迎界面和游戏主页（右上角的鼠鼠是bgm开关，dj鼠为开，哭泣鼠为关），游戏的主题我们采用萌系风格来设计，鼠鼠这个叠叠词也适配了萌系主题风格，"有头脑"谐音为"有“骰“脑"，因为我们觉得这游戏还是要有一点骰脑的（欢迎界面中的K班元素和右下角的吃瓜k鼠，都体现了我们K班的特色！！！）

2.规则

3.三种游戏模式

本地鼠

人机鼠

在线鼠

4.排行鼠

创新点：

1. 采用动态小鼠鼠作为按钮

2. 点击按钮时具有班级特色音效

3. 欢迎页面左上角带有K班级元素，以及右下角有只吃瓜ing的K鼠

三、编程实现

3.1 网络接口的使用

利用微信自带的获取用户信息的接口，在用户授权的情况下获取用户的昵称等信息，用于绑定数据库中的得分。

用户授权登录接口

wx.getUserProfile({
            desc: '必须授权才能继续使用', // 必填 声明获取用户个人信息后的用途，后续会展示在弹窗中
            success:(res)=> { 
                console.log('授权成功', res);
                app.globalData.userInfo=res.userInfo;
                wx.connectSocket({
                  url: app.globalData.serverurl,
                });
            },
            fail:(err)=> {
                console.log('授权失败', err);
            }
        })

用了websocket接口实现在线对战所需的全部联网功能，排行榜的数据获取

websocket连接接口

wx.connectSocket({
      url: app.globalData.serverurl,
      success: () => {
       console.log('建立 WebSocket 连接成功:);
      },
      fail: (error) => {
        console.error('建立 WebSocket 连接失败:', error);
      },
    });

websocket发送数据接口

wx.sendSocketMessage({
      data: socketMsg[i]//发送socketMsg[i]数据
});

websocket接收数据接口

wx.onSocketMessage((result) => { 
      console.log(result)//接收result数据并打印
});

websocket关闭连接接口

wx.onSocketClose((result)=> {
     //断开连接后执行的代码
})

3.2 代码组织与内部实现设计（类图）

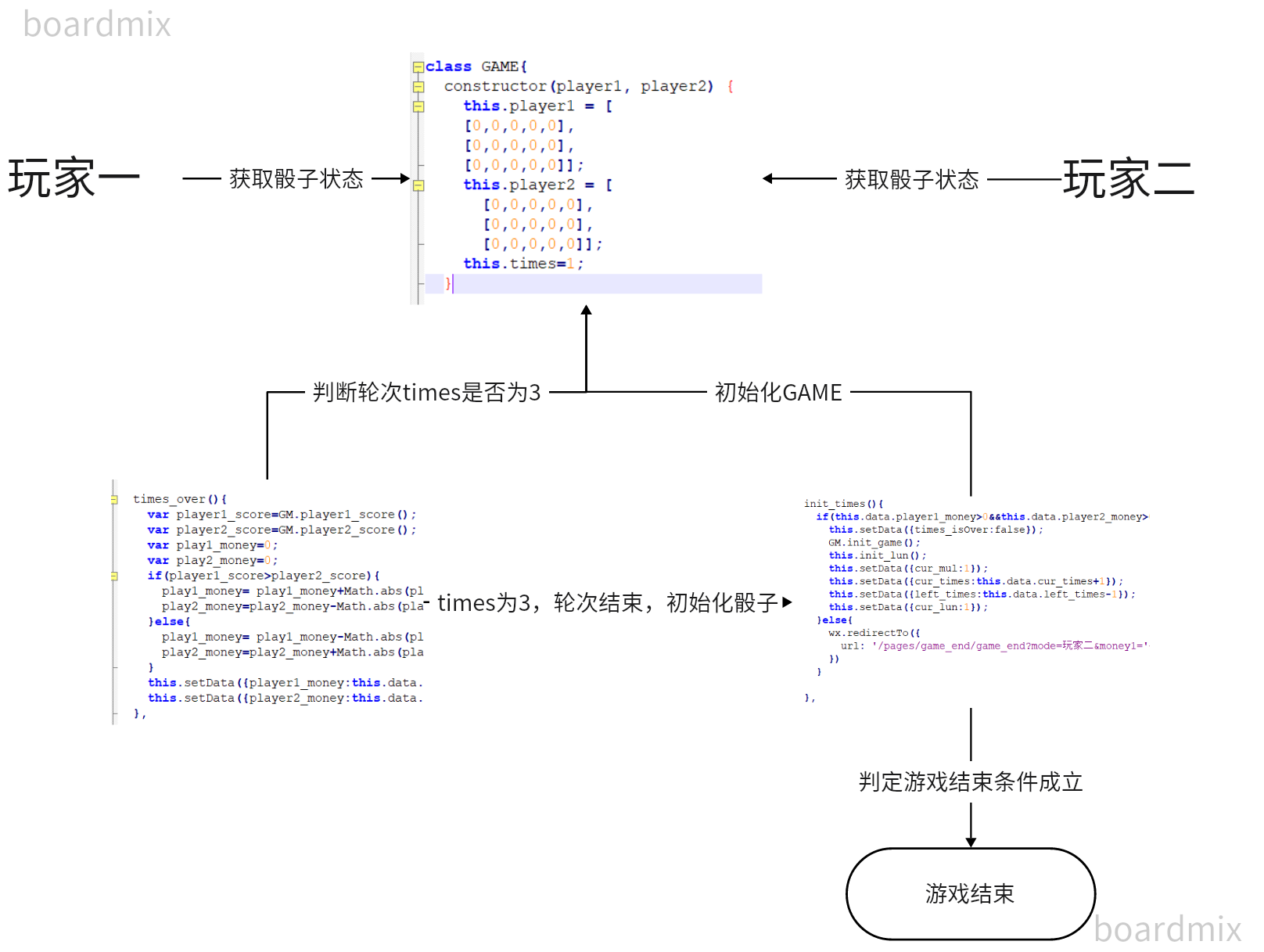
实现思路：定义一个游戏对象GAME，维护整局游戏双方的骰子状态，轮次和分数计算，双方玩家能从GAME获取当前双方的骰子区，锁定区。并能在结算时获取双方得分。外部函数times_over()用于计算双方筹码的改变并作用于页面显示，init_times()用来初始化GAME以及判断游戏是否结束，若游戏结束则跳转结算页面。

3.3 说明算法的关键与关键实现部分流程图

关键一：

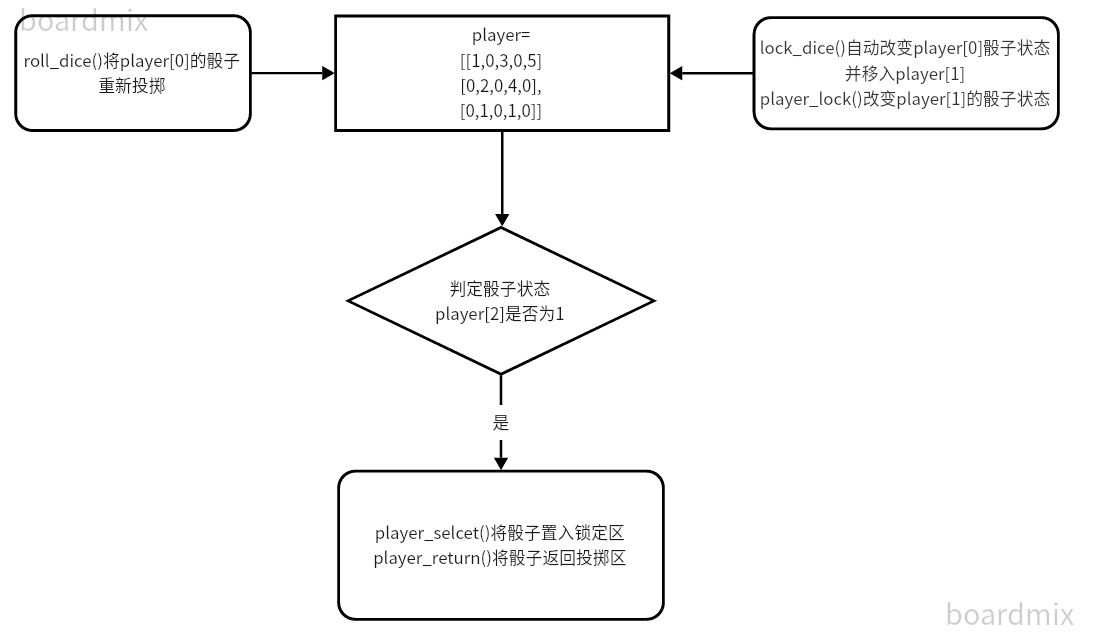
算法的关键在于控制双方骰子的状态，即骰子在哪个区，骰子的区域是否能改变，骰子是否需要在重掷的时候改变等等。player是一个二维数组，player[0]为投掷区，player[1]为锁定区，player[2]为状态区,0表示未锁定，1表示锁定。可以用player_select()的方法将改变骰子的状态，置入锁定，player_return()方法将未锁定的骰子从锁定区移入投掷区，player_lock()方法将锁定区的骰子状态改为不可转变和移动,lock_dice()方法则用于三阶段自动锁定所有骰子。role_dice()则是将投掷区的骰子重掷。

流程图与代码实现如下：

  role_dice(){
    this.times=this.times+1;
      for(let i=0;i<5;i++){
        if(this.player1[0][i]!=0){
          this.player1[0][i]=Math.floor(Math.random()*6)+1;
        }
        if(this.player2[0][i]!=0){
          this.player2[0][i]=Math.floor(Math.random()*6)+1;
        }
      }
    return this.times;
  }
  lock_dice(){
    for(let i=0;i<5;i++){
      if(this.player1[0][i]!=0){
        this.player1[1][i]=this.player1[0][i];
        this.player1[0][i]=0;
      }
      if(this.player2[0][i]!=0){
        this.player2[1][i]=this.player2[0][i];
        this.player2[0][i]=0;
      }
    }
  }
  player1_select(x){
    if( this.player1[0][x]!=0){
      this.player1[1][x]=this.player1[0][x];
      this.player1[0][x]=0;
    }
    return;
  }
  player1_return(x){
    if(this.player1[2][x]==0&& this.player1[1][x]!=0){
      this.player1[0][x]=this.player1[1][x];
      this.player1[1][x]=0;
    }
    return;
  }
  player1_lock(){
    for(var i=0;i<5;i++){
      if(this.player1[1][i]!=0){
        this.player1[2][i]=1;
      }
    }
    return;
  }

关键二：

为了能够让AI在每次选择骰子时可以选择出最优结果，我们通过递归将选择每种骰子情况的期望分（期望分是指选择该种骰子情况后整局即三轮投掷锁定的平均得分）计算存入到一维六叉树expect数组中。之后AI在选择骰子时可通过查询expect数组中期望值最大的情况，从而选出最优骰子结果。通过这种方式可以最大程度的避免AI选错骰子。
举个例子：
例如第一轮投掷锁定中，可选骰子为[1, 1, 2, 2, 3]，通过个人主观判断，可能的选择情况是[1, 1, 2, 2]或者[1, 2, 3]，因为我们主观认为应该去选择具有奖励分的骰子情况，但是根据期望分（也就是整局平均得分）来选择的话，应该是选择[3]，是不是很惊讶，这似乎有点不符合我们的主观认识？是不是错了呀？
不急，接下来解释一下：

1. 选择[1, 1, 2, 2]：
   在选择这种骰子情况后，它的最终骰子只能是[1, 1, 2, 2, 1 or 2 or 3 or 4 or 5 or 6]六种情况中的一种，那它的得分也就只能是[27, 28, 19, 20, 21, 22]六种中的一种，那它的期望分（也就是整局平均得分）是不是就是expect[266] = (27 + 28 + 19 + 20 + 21 + 22)/6 = 22.833。

2. 选择[1, 2, 3]：
   在选择这种骰子情况后，他的最终骰子就是6 * 6 = 36（因为剩下两个骰子，每个骰子有6种选择）种情况，[1, 2, 3, 1 or 2 or 3 or 4 or 5 or 6， 1 or 2 or 3 or 4 or 5 or 6]，它的得分是[18,19,20,41,12,13,19,20,21,42,13,14,20,21,22,43,14,15,41,42,43,44,75,46,12,13,14,75,16,17,13,14,15,46,17]36种中的一种，那它的期望分（也就是整局平均得分）是不是就是expect[51] = (18+19+20+41+12+13+19+20+21+42+13+14+20+21+22+43+14+15+41+42+43+44+75+46+12+13+14+75+16+17+13+14+15+46+17)/36 = 26.333。（是不是觉得列这36种情况很累，其实一点不累，直接从expect数组中复制出来就好了，很方便的哈哈哈哈，对了expect中的266和51是通过骰子计算的，266 = ((((0 * 6)+1) * 6+1) * 6+2) * 6+2 , 51 = (((0 * 6)+1) * 6+2) * 6+3）

3. 那么，通过相同的计算方法我们得到选择[3]的期望分是29.978，所以在[1, 1, 2, 2, 3]中，应该选择[3]。（这种选择骰子的方式也太天才了hhhhhhh）

递归求解一维六叉树代码实现如下：

def get_score(a):
    # 对输入的骰子点数列表a进行升序排序
    a.sort()
    # 计算骰子点数总和
    basic = sum(a)
    price = 0
    # 判断是否满足特殊规则并返回相应的分数
    price = judge_shun(a)  # 判断是否为顺子
    if price != 0:
        return basic + price
    elif all(x == a[0] for x in a):  # 判断是否为五骰相同
        return basic + 100
    elif judge_four(a) == 1:  # 判断是否为四骰相同
        return basic + 40
    elif judge_hulu(a) == 1:  # 判断是否为葫芦
        return basic + 20
    elif judge_three(a) == 1 or judge_two(a) == 1:  # 判断是否为三条或两对
        return basic + 10
    # 若都不满足以上规则，返回基本总和分数
    return basic

def tree_push(x1, x2, x3, x4, x5, num):
    # 将分数num存储在一维数组expect中的指定位置
    index = ((((0 * 6 + x1) * 6 + x2) * 6 + x3) * 6 + x4) * 6 + x5
    expect[index] = num

def get_all_expect(depth, index):
    # 递归计算期望值
    if depth >= 5:
        return
    for i in range(1, 7):
        get_all_expect(depth + 1, index * 6 + i)
        expect[index] += expect[index * 6 + i]
    expect[index] /= 6.0

def init_expect():
    a = [0] * 5
    # 创建一个5维的数组res，用于存储每个骰子点数组合对应的分数

    for i1 in range(6):
        for i2 in range(6):
            for i3 in range(6):
                for i4 in range(6):
                    for i5 in range(6):
                        # 将点数加1并计算对应的分数，存储在res中
                        a[0] = i1 + 1
                        a[1] = i2 + 1
                        a[2] = i3 + 1
                        a[3] = i4 + 1
                        a[4] = i5 + 1
                        # 将分数存储在expect一维数组中
                        tree_push(i1 + 1, i2 + 1, i3 + 1, i4 + 1, i5 + 1, get_score(a))

    # 计算期望值
    get_all_expect(0, 0)

关键三：

在能够正确选择最优骰子后，我们还需要让AI能够根据不同情况去选择最优的倍率，但是如果仅仅考虑双方分差的话，由于这是一个零和博弈的问题，这样倍率的选择不是0就是3，所以要引入其他变量，我们引入双方筹码差，当前骰子分差，剩余局数3个变量，通过alpha，beta，gamma三个参数来帮助倍率选择的决策，而这三个参数我们通过用遗传算法来优化，。

代码实现如下：

 /*倍率决策函数*/
  mul_power(chips_sub, scores_sub, round_sub) {
    if (chips_sub > 0) {
        chips_sub = Math.log(Math.abs(chips_sub));
    } else if (chips_sub < 0) {
        chips_sub = -Math.log(Math.abs(chips_sub));
    }
    if (round_sub !== 0) {
        round_sub = Math.log(Math.abs(round_sub));
    }
    if (-10 <= chips_sub && chips_sub <= 10 && 0 <= round_sub && round_sub <= 10) {
        var judge = alpha * chips_sub + beta * scores_sub + gama * round_sub;
        if (judge > 100) {
            return 3;
        } else if (judge > 0) {
            return 2;
        } else if (judge > -100) {
            return 1;
        } else {
            return 0;
        }
    }
    return 0;
  }
/*生成所有组合情况*/
generateIndexCombinations(arr) {
    const indexes = [];
    for (let i = 0; i < arr.length; i++) {
      if (arr[i] !== 0) {
        indexes.push(i);
      }
    }
    const combinations = [];
    function backtrack(start, currentCombo) {
      combinations.push([...currentCombo]);
      for (let i = start; i < indexes.length; i++) {
        currentCombo.push(indexes[i]);
        backtrack(i + 1, currentCombo);
        currentCombo.pop();
      }
    }
    backtrack(0, []);
    return combinations;
  }
/*找到期望最大的骰子组合*/
findMaxScoreIndexCombination(arr) {
    const indexCombinations = this.generateIndexCombinations(arr);
    let maxScore = -Infinity;
    let maxScoreIndexCombination = [];
  
    for (let i = 0; i < indexCombinations.length; i++) {
      const currentIndexCombination = indexCombinations[i];
      const lockedDice = currentIndexCombination.map(index => arr[index]);
      const score=this.calculate_expect(lockedDice);
      if (score > maxScore) {
        maxScore = score;
        maxScoreIndexCombination = currentIndexCombination;
      }
    }
    return maxScoreIndexCombination;
  }
/*期望得分查找*/
  calculate_expect(dice) {
    let locked_dice = Array.from(dice);
    const l = locked_dice.length;
    let index = 0;
    for (let i = 0; i < 5; i++) {
      if(this.player2[1][i]==0){
        continue;
      }
      index *= 6;
      index += this.player2[1][i];
    }
    for (let i = 0; i < l; i++) {
      if(locked_dice[i]==0){
        continue;
      }
      index *= 6;
      index += locked_dice[i];
    }
    return this.expect[index];
  }
/*倍率获取*/
  getmult(chips_sub,round_sub){
    var scores_sub=this.get_expect(this.player2[1])-this.get_expect(this.player1[1]);
    var mul = this.mul_power(chips_sub,scores_sub,round_sub);
    return mul;
  }

3.4 贴出重要的/有价值的代码片段并解释

重要片段实现想法：

为了让AI的倍率决策足够好，我们需要填入足够完美的三个参数，但这三个参数靠自己瞎猜没辙，数学分析什么的也绞尽脑汁也分析不出什么个所以然，这参数的好坏是非常有价值的，它决定了我们AI的智商，所以我们通过遗传算法来找这三个参数。

重要片段实现思路：

我们通过模拟10000局游戏去优化这三个参数。在游戏中，两位玩家的骰子选择方式均采用AI方式，而倍率选择方式略有不同。
对于玩家一：我们通过遗传算法中随机生成的alpha, beta, gamma为玩家一进行倍率选择。
对于玩家二：当选择的骰子期望分高于玩家一时选择3倍，反之0倍。
在这种游戏模式下，去跑10000局，然后将该参数的游戏胜率作为适应度，从而去迭代优化三个参数。在得到一个较为优秀的值后，将这三个参数用于玩家二的倍率选择，然后继续迭代优化，从而获取到最优秀的参数，并用于我们的AI倍率选择中。（在经过了数天的优化，我们最终也是得到了一个较为优秀的值，不枉费我们多天的努力哈哈哈哈。）

代码实现如下：

def get_fitness(win_round):
      win_rounds = [0] * POP_SIZE
      for i in range(len(win_round)):
          win_rounds[i] = win_round[i]
          win_rounds[i] /= 1000
      return win_rounds

def translateDNA(pop):
    dna_size = (3 * DNA_SIZE)
    # 划分pop矩阵以提取alpha、beta和gamma部分
    alpha_pop = pop[:dna_size // 3]
    beta_pop = pop[dna_size // 3: 2 * (dna_size // 3)]
    gamma_pop = pop[2 * (dna_size // 3):]

    # 将二进制编码转换为十进制
    alpha = (alpha_pop.dot(2 ** np.arange(dna_size // 3)[::-1]) / float(2 ** (dna_size // 3) - 1)) \
            * (alpha_BOUND[1] - alpha_BOUND[0]) + alpha_BOUND[0]
    beta = (beta_pop.dot(2 ** np.arange(dna_size // 3)[::-1]) / float(2 ** (dna_size // 3) - 1)) \
           * (beta_BOUND[1] - beta_BOUND[0]) + beta_BOUND[0]
    gamma = (gamma_pop.dot(2 ** np.arange(dna_size // 3)[::-1]) / float(2 ** (dna_size // 3) - 1)) \
            * (gamma_BOUND[1] - gamma_BOUND[0]) + gamma_BOUND[0]

    return alpha, beta, gamma


def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
    new_pop = []
    for father in pop:  # 遍历种群中的每一个个体，将该个体作为父亲
        child = father  # 孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:  # 产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]  # 再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE * 3)  # 随机产生交叉的点
            child[cross_points:] = mother[cross_points:]  # 孩子得到位于交叉点后的母亲的基因
        mutation(child)  # 每个后代有一定的机率发生变异
        new_pop.append(child)

    return new_pop


def mutation(child, MUTATION_RATE=0.003):
    if np.random.rand() < MUTATION_RATE:  # 以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE * 3)  # 随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point] ^ 1  # 将变异点的二进制为反转

def select(pop, fitness):    # nature selection wrt pop's fitness
    all_sum = sum(fitness)
    for i in range(len(fitness)):
        fitness[i] /= all_sum
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=fitness)
    return pop[idx]


ct=0
for _ in range(N_GENERATIONS):  # 迭代N代
        ct += 1
        print(f"迭代次数:{ct}")
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))#种群繁衍
        wt_ct = 1
        for i, mul in enumerate(pop):
            alpha, beta, gamma = translateDNA(mul)#基因编码
            win_round[i] = play(alpha, beta, gamma)#返回胜率
            print(f"第{ct}代;第{wt_ct}个权重")
            wt_ct += 1
        fitness = get_fitness(final_win_round)#将胜率转换为选择的概率
        pop = select(pop, fitness)  # 选择生成新的种群
    print_info(pop)#输出最优基因型

3.5 性能分析与改进

我们采用了微信小程序开发工具自带的真机调试功能，发现加载图片的时候时间消耗比较大，经常出现白屏的现象。我们的改进思路是把一些用到比较的多的组件图片存到本地，例如返回按钮，然后对所有图片进行压缩，避免图片过大造成的额外开销。我们程序消耗最大的函数应该是人机计算最大得分期望的组合findMaxScoreIndexCombination()，因为它要把所有组合情况都算出来。

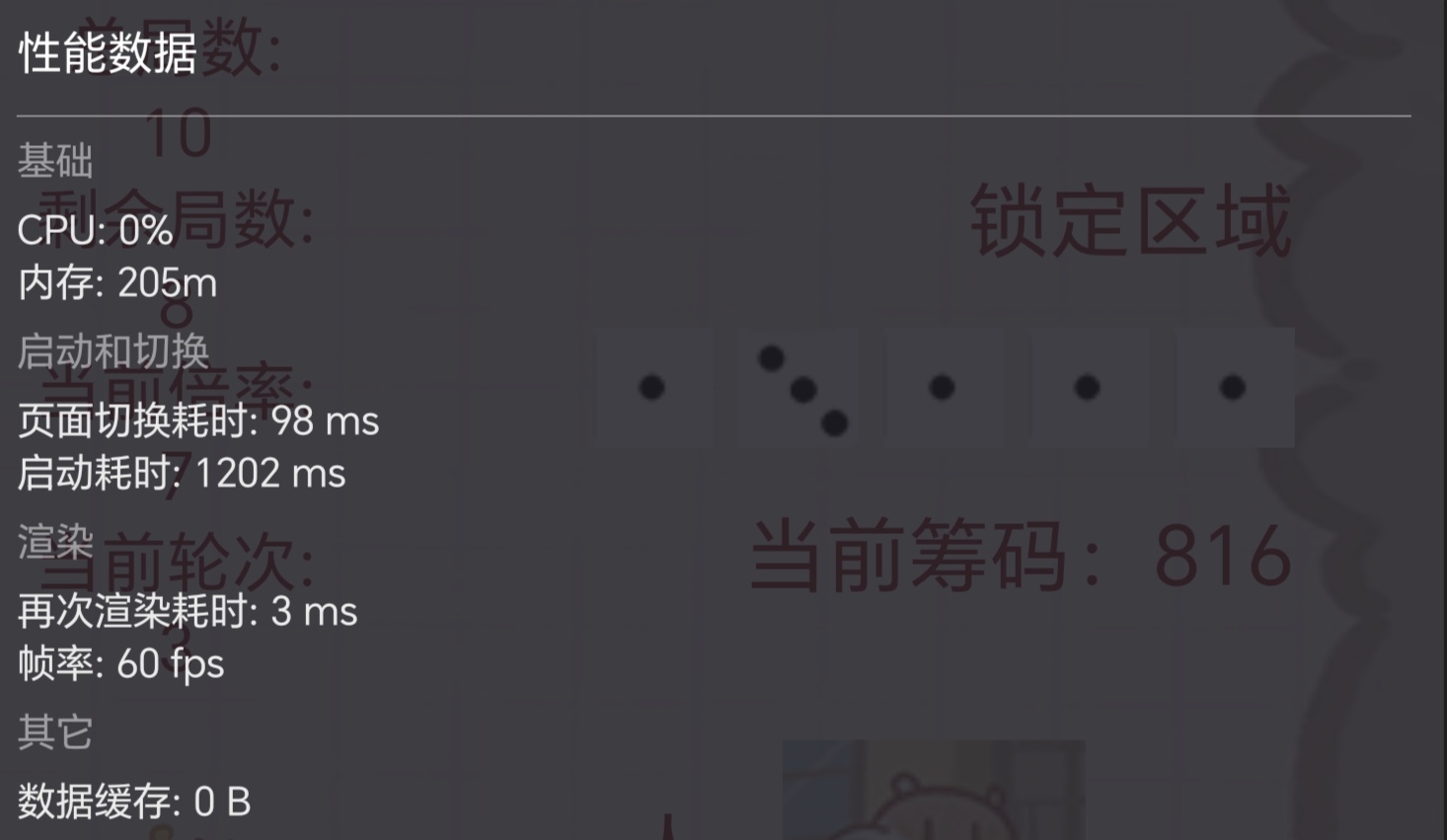
还有就是遗传算法跑的时间有亿点久，但看到CPU利用率不高，于是就采用多进程优化。

代码实现如下：

def process_iteration(i, mul, ct, win_round):
    alpha, beta, gamma = translateDNA(mul)
    result = play(alpha, beta, gamma)

    with win_round.get_lock():
        win_round[i] = result

pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 3))  # matrix (POP_SIZE, DNA_SIZE)
    ct = 0
    num_processes = multiprocessing.cpu_count()  # 获取可用的 CPU 核心数
    for _ in range(N_GENERATIONS):  # 迭代N代
        ct += 1
        print(f"迭代次数:{ct}")
        processes = []  # Define the processes list
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
        win_round = multiprocessing.Array('i', [0] * len(pop))
        for i, mul in enumerate(pop):
            p = multiprocessing.Process(target=process_iteration, args=(i, mul, ct, win_round))
            processes.append(p)
        while processes:
            wait_p=[]
            for j in range(num_processes):
                if processes:
                    p = processes.pop(0)
                    wait_p.append(p)
                    p.start()

            for p in wait_p:
                p.join()
        # 获取修改后的 win_round 值
        final_win_round = list(win_round)
        fitness = get_fitness(final_win_round)
        pop = select(pop, fitness)  # 选择生成新的种群
    print_info(pop)

3.6 单元测试

我们采用pycharm自带的unittest库函数对游戏里的人机的倍率选择和骰子选择进行了测试，检测人机是否能够准确的选择。

代码实现如下：

import itertools
import unittest
from game import mul_power
from cal_expect import expect,init_expect

init_expect

dice = [[1, 2, 3, 4, 6], [1, 2, 3, 4, 5], [1, 1, 2, 2, 3], [3, 3, 3, 4, 4],
        [4, 4, 4, 5, 6], [5, 5, 5, 5, 6], [6, 6, 6, 6, 6], [1, 1, 2, 4, 6],
        [1, 2, 4, 5, 6], [4, 5, 5, 6, 6], [5, 5, 5, 6, 6]]
should_choose_dice = [[1, 2, 3, 4], [1, 2, 3, 4, 5], [3], [3, 3, 3], [4, 4, 4],
                      [5, 5, 5, 5], [6, 6, 6, 6, 6], [4], [4, 5, 6], [5, 5, 6, 6],
                      [5, 5, 5, 6, 6]]
expects = [48.5, 75.0, 29.978395061728396, 38.22222222222222, 41.22222222222222, 73.5, 130.0, 30.978395061728392,
           35.333333333333336, 38.833333333333336, 47.0]
chips_sub = [1000, 2000, -3100, 5000, -4200]
score_sub = [10, 20, 30, 40, 50]
rem_innings = [1000, 1200, 2300, 2100, 3400]
multi_power = [3, 3, 3, 3, 3]


def calculate_expect(test_dice):
    max_expect = []
    m_expect = -1
    for i in range(6):  # 0到count个骰子
        combinations = itertools.combinations(test_dice, i)  # 生成i个骰子的组合
        for combination in combinations:
            index = 0
            l = len(combination)
            for j in range(l):
                index *= 6
                index += combination[j]
            if expect[index] > m_expect:
                m_expect = expect[index]
    max_expect.append(m_expect)
    return max_expect


def choose_Dice(test_dice):
    m_expect = -1
    choose_dice = []
    max_choose_dice = []
    for i in range(6):  # 0到count个骰子
        combinations = itertools.combinations(test_dice, i)  # 生成i个骰子的组合
        for combination in combinations:
            index = 0
            l = len(combination)
            for j in range(l):
                index *= 6
                index += combination[j]
            if expect[index] > m_expect:
                m_expect = expect[index]
                choose_dice = combination
    choose_dice = list(choose_dice)
    max_choose_dice.append(choose_dice)
    return max_choose_dice


class Mytest(unittest.TestCase):

    def test_calculate_expect(self):

        dice_expect = []
        for test_dice in dice:
            dice_expect += calculate_expect(test_dice)
        self.assertEqual(dice_expect, expects)

    def test_choose_Dice(self):

        choosed_dice = []
        for test_dice in dice:
            choosed_dice += choose_Dice(test_dice)
        self.assertEqual(choosed_dice, should_choose_dice)

    def test_mul_power(self):

        power = []
        for i in range(5):
            power.append(mul_power(-108.79908256525293, 158.38854064873104, -47.57462427464868,
                                   chips_sub[i], score_sub[i], rem_innings[i]))
        self.assertEqual(multi_power, power)


if __name__ == '__main__':
    unittest.main()

测试结果：

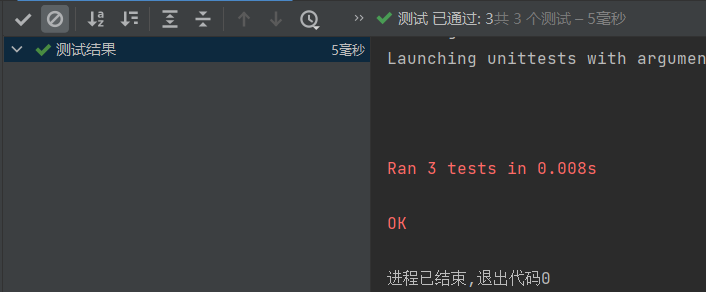
测试思路：

给出多种骰子情况（包含各种奖励分骰子，也包括没有奖励分骰子），并将骰子、倍率、期望的正确选择情况存入列表中，然后与人机返回的选择情况相比较，若相同则说明测试成功，反之失败。

3.7 贴出GitHub的代码签入记录，合理记录commit信息

四、总结反思

4.1 本次任务的PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	30
· Estimate	· 估计这个任务需要多少时间	8255	9360
Development	开发	8180	9275
· Analysis	· 需求分析 (包括学习新技术)	2000	2400
· Design Spec	· 生成设计文档	60	60
· Design Review	· 设计复审	30	45
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	60
· Design	· 具体设计	300	400
· Coding	· 具体编码	5640	6020
· Code Review	· 代码复审	60	60
· Test	· 测试（自我测试，修改代码，提交修改）	60	60
Reporting	报告	75	85
· Test Report	· 测试报告	15	25
· Size Measurement	· 计算工作量	30	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	· 合计	8285	9390

4.2 学习进度条（每周追加）

112101129陈佳俊：

第N周	新增代码（行）	累计代码（行）	本周学习耗时(小时)	累计学习耗时（小时）	重要成长
1	300	300	42	42	学习了微信小程序的开发流程，能开始开发微信小程序
2	4000	4300	60	102	学习了JS文件，前端的程序编写，人机AI算法模型，完成了本地对战，人机对战的功能。
3	4000	8300	72	174	学习了websocket网络编程的使用，后端nodejs的编写，完成在线对战和排行榜的功能

102101518吴鑫雄：

第N周	新增代码（行）	累计代码（行）	本周学习耗时(小时)	累计学习耗时（小时）	重要成长
1	0	0	23	23	了解原型设计工具，学会运用ps，原型设计能力提升
2	467	467	61	84	遗传算法，编写游戏代码
3	54	521	6	90	单元测试，视频制作

4.3 最初想象中的产品形态、原型设计作品、软件开发成果三者的差距如何？

最初想象中的产品形态和我们的原型设计作品差不多，基本一模一样，甚至效果可能更好，比如在在线鼠中，我们多加了创建房间、加入房间、在线匹配三种选择，更加符合联机模式的需求。原型设计产品能具象化我们的想象，然后设计过程中就会发现”欸，这里加点东西会不会好点，多个功能会不会更好“，这些类似的情景。然后是软件开发成果上确实无法做到和原型设计中一模一样，因为有些东西在原型设计中很难考虑到（可能是我们自身的问题），例如我们排行榜原型的布局，在微信小程序上我们无法实现（太菜了喵）。在线对战没有考虑到怎么匹配玩家，在最终的产品上加一点，减一点，虽然如此，但最终产品确实和我们想象中的产品有十分甚至九分相似。

游戏进行中的相关说明：

1. 进入游戏界面后，点击投掷区域里的骰子即可选择

2. 选择骰子后，若发现选择了错误骰子，可以点击锁定区域里的错误骰子（在锁定区域四个字右边还没有“已锁”两个字的时候），即可重新选择正确骰子

3. 无误的选择骰子后，可以点击屏幕中央下方的木鱼鼠进行锁定骰子,这时锁定区域四个字右边会出现“已锁”两个字

4. 锁定骰子后，会出现3种倍率以供选择，直接点击倍率即可选择

5. 游戏结束后，会自动跳转到结算界面

6. 玩家头像旁边的摸肚肚鼠是托管按钮，点击即可托管

ps：左下角的鼠鼠是bgm开关

创建房间以及托管功能如下：

在线匹配以及托管功能如下：

4.4 评价你的队友

112101129陈佳俊：

我的队友真的能让我感到惊喜，他的原型设计确实能惊艳到我，比我这种直男审美要好，而且原型的交互，界面也确实不错，没想到能做得这么好。还有就是AI算法模型的参数需要用遗传算法来找嘛，我跟我的队友说了算法模型和思路，没想到他竟然真的实现了（虽然写了挺多bug的）。他的这种行动力确实值得我去学习，要说有什么值得改进的，估计就是多点讨论吧，编写算法模型时理解错我的意思导致算法写错了（也许是我表达不好的问题），然后少写bug（

102101518吴鑫雄：

我只能说我的队友很强（大拇指）！！！他的学习能力和执行效率都很高，在之前从未接触过开发工具和开发语言的情况下，依旧能在较短的时间完成原型设计的代码实现。以及联机模式的代码编写；然后他的团队意识也很好，在作业完成过程中，会帮我一起找bug改bug，还一起调参数，并且因为遗传算法跑的很慢，用他的电脑一起跑（开多进程跑，CPU占用率很高，将自己的电脑贡献给这个作业...）。总之，这次作业可以说是在他的带领下完成的，他有很多我指得学习的地方。然后值得改进的地方，也是再多点讨论吧。

4.5结对编程作业心得体会

112101129陈佳俊：

最想说的就是太折磨了。。。无论是开发工具还是开发语言，代码编写什么的，从头折磨到尾＞﹏＜

1. 首先是开发工具和开发语言，我全都没有用过！！！！简直就像路都不会走就叫我们去跑1km。我只能从网上找到一些资源，学一半做一半，最折磨的当属学习语言，开发时根本不知道有什么特性能用，有什么功能好使，还有满屏的语法错误，学习语言最痛苦的就是要花大量时间学习前人的语法，改正自己的代码。要是没有GPT，我们要花多一倍的时间在无意义的查错上。

2. 还有就是微信小程序的开发，一开始打算做小游戏的，但我们发现小游戏要上线十分困难，要签一堆证书，软著等等，还要有资质，等这些东西办完下来，早就不知道过deadline多久了，然后我们打算换回小程序，但一旦你选择了小游戏的服务类目你就改不回其他类目了，只能注销账号重新注册了。

3. 还有就是联机功能，首先最大的难点是服务器和SSL证书，没钱哇，还有就是你小程序要是有联机在线这类东西的话，你审核是很难通过的，所以上线的小程序我们不得不砍掉在线的功能，但这部分程序我们会放在GitHub上。但最主要的是我们后端程序没有完善的安全检验系统，也就是我们后端防不住恶意的请求，有人稍微捣乱下就能使游戏乱掉。。（太菜了不会防）

4. 还有的AI算法模型的编写，真的是一堆bug和莫名其妙的错误，改bug改到头疼，好不容易改完了发现跑遗传算法所需的时间有那么亿点点久，就采用了多进程优化100%榨干CPU，跑完后发现参数不是不理想，是离谱！相关性都是错的，又找了很久的bug，发现bug修复bug，没有用，又再找。。。反反复复，最终终于能跑出正确相关性的参数了，但胜率甚至不如傻瓜式AI？？？？最后发现胜利函数参数限制了发挥。。。。跑了几天总算有个能用的了。（太折磨了）

5. 网络编程调试也挺折磨的，经常因为各种同步问题造成莫名其妙的错误，包括但不限于倍率无限叠加，锁定锁到下一局，锁定区骰子自己走回投掷区，贷款对决。。。。修起来也头疼，现在可能还有隐藏的bug没被发现

6. 小程序今年上线是要备案的，但个人备案我不好说，过不了，怎么想都过不了吧，驳回原因不是什么小程序名称备注不对，就是小程序内容不符合个体性质，需上传企业资质，我。。。。

怎么说呢，折磨是真折磨，但也能让我学到挺多东西，熟悉开发流程，就是没少熬夜，有点费身体。但这一切都是值得的，对吗？执拗的花朵永远不会因暴雨而褪去颜色，你的决心也一定能在绝境中绽放真我

102101518吴鑫雄：

这次的作业难度说实话是有一定难度的，不管是原型的设计，前后端代码的编写，遗传算法的运用以及联机模式的实现都是具有一定的难度，每个环节都在折磨着我们。

1. 原型的设计：

   为了能够设计出一个能够吸引眼球的原型。着实是非常折磨的，在刚开始设计了几种原型，但感觉都没有很创新，就都pass掉了。最后通过借鉴学长学姐们的作业，我们用谐音梗的形式确定了我们的小程序名字，也就确定了大致风格，之后就是找素材，这也是一大折磨之处，找图片是难事，找到图片后的处理也是难事，要么是图片有水印，要么是背景颜色不符合，要么是图片大小不统一等等，反正就是折磨。

2. 游戏编写：

   能满足本地对战的游戏编写折磨倒是没那么大，但是能用于计算适应度函数的游戏编写属实折磨。本地对战的游戏编写，我是在gpt编写完的大致框架下去修改的（gpt还是不够聪明，错误很多），大致改了1.5小时吧。之后就是在本地对战游戏模式下继续修改，让其能够满足适应度函数要求，在这个过程里，依旧有一堆bug（当然，这个时候我也理解错了我队友的意思，把代码思路写错了），这边我又改了一天吧好像（零零碎碎的一天）。

3. 遗传算法：

   在这次作业之前，我没有自主实现过遗传算法，所以我知道这也是一个难题。但是为了作业的顺利完成，我只能硬着头皮跟着csdn先复现这个算法，然后再慢慢的去修改目标函数、适应度函数、种群、个体等等。就是在修改的时候，我又一次被折磨了，会出现各种的bug，修改完一个bug又出现一个bug，永无止境的bug(啊啊啊啊～)。好在我的队友前来帮助，最后才解决掉所有的bug（nice~）。（发现我写代码bug好多...）

总之，在这次作业里面，可以说是在折磨中进步，受到了不少折磨，也收货了不少知识，掌握了墨刀工具（还有到处找素材的能力！）、学会了使用遗传算法优化问题、能够编写游戏代码，以及懂得了ps和剪映的使用。最后在小程序完成的时候成就感满满！！！

[刘炜祺102101513]

这个页面真的好看，满昏

[杨宇晗102101517]

鼠鼠我鸭，被人机薄纱了捏