L1-5 最大公约数和最小公倍数

202321332016 林伟坤软件23 2023-11-07 18:15:50

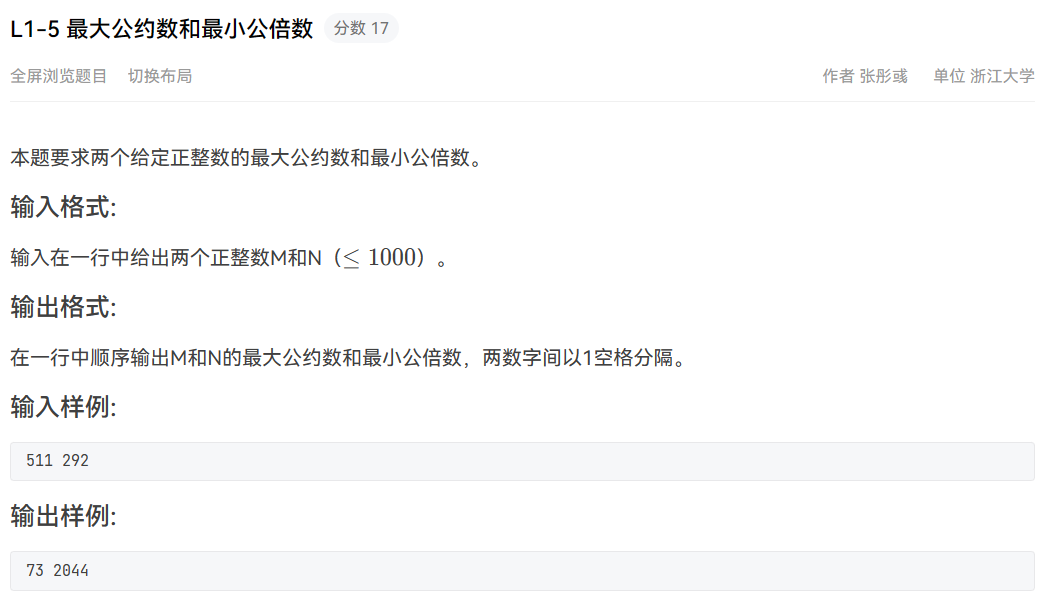
这道题是一个经典的数学问题，要求我们求出两个给定正整数的最大公约数和最小公倍数。最大公约数是指能够同时整除两个数的最大的正整数，最小公倍数是指能够被两个数同时整除的最小的正整数。有一个重要的性质是，两个数的乘积等于它们的最大公约数和最小公倍数的乘积，即

MN=gcd(M,N)×lcm(M,N)

为了求出最大公约数，我们可以使用一个古老而有效的算法，叫做辗转相除法或欧几里德算法。这个算法的思想是，如果

M≥N，那么

gcd(M,N)=gcd(N,M mod N)

其中M mod N 表示M除以N的余数。这样，我们可以不断地用余数替换较大的数，直到余数为0，此时较小的数就是最大公约数。例如，要求

60 和24 的最大公约数，我们可以这样计算：

gcd(60,24)

=gcd(24,60mod24)

=gcd(24,12)

=gcd(12,24mod12)

=gcd(12,0)

=12

为了求出最小公倍数，我们可以利用上面提到的性质，用两个数的乘积除以它们的最大公约数，即

lcm(M,N)=gcd(M,N)MN 。

例如，要求60 和24 的最小公倍数，我们可以这样计算：

lcm(60,24)=gcd(60,24)60×24=1260×24=120

下面是用C语言实现这个算法的一种可能的代码：

#include <stdio.h>

// 定义一个函数，用辗转相除法求两个数的最大公约数
int gcd(int m, int n) {
    int r; // 用来存储余数
    while (n != 0) { // 当余数不为0时，重复以下步骤
        r = m % n; // 计算余数
        m = n; // 用较小的数替换较大的数
        n = r; // 用余数替换较小的数
    }
    return m; // 当余数为0时，返回较小的数，即最大公约数
}

// 定义一个函数，用两数乘积除以最大公约数求两个数的最小公倍数
int lcm(int m, int n) {
    return m * n / gcd(m, n); // 利用性质，直接返回结果
}

int main() {
    int m, n; // 定义两个变量，用来存储输入的两个正整数
    printf("请输入两个正整数，以空格分隔：\n"); // 提示用户输入
    scanf("%d %d", &m, &n); // 从标准输入读取两个整数
    printf("这两个数的最大公约数是%d，最小公倍数是%d\n", gcd(m, n), lcm(m, n)); // 调用函数，输出结果
    return 0; // 程序正常结束
}

这段代码的输入和输出格式符合题目要求，可以通过测试。如果您想了解更多关于这个问题的信息，您可以参考以下网页：

希望这篇博文对您有所帮助，如果您有任何问题或建议，欢迎在下方留言。谢谢您的阅读！

...全文