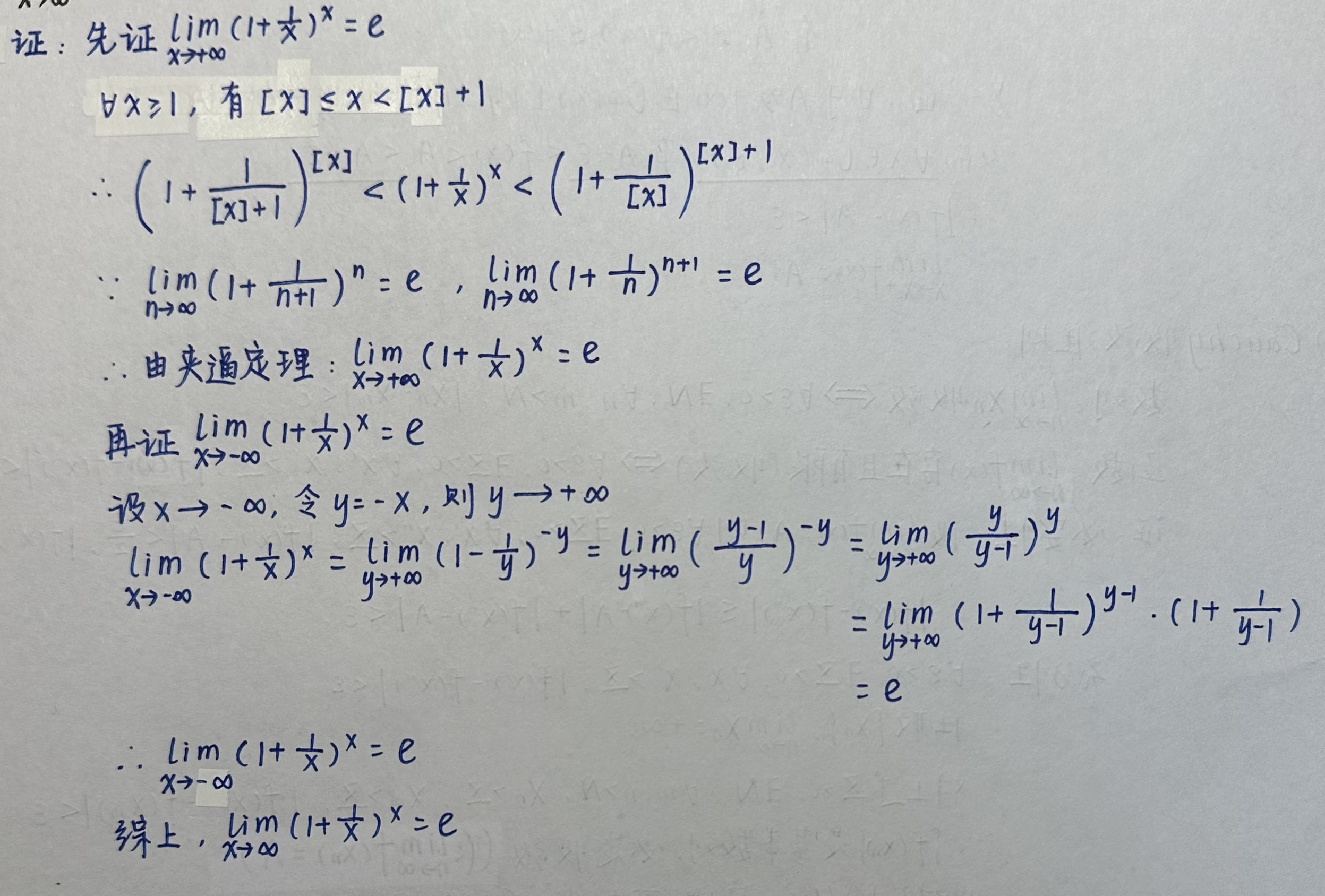数学分析——函数极限四节笔记

[mcn18065151636]

目录

1、函数极限的概念

2、函数极限的性质

3、函数极限存在的条件 

4、两个重要极限 

---

1、函数极限的概念

1）x趋于∞时函数的极限：

 2）x趋于+∞时函数的极限：

 3）x趋于-∞时函数的极限：

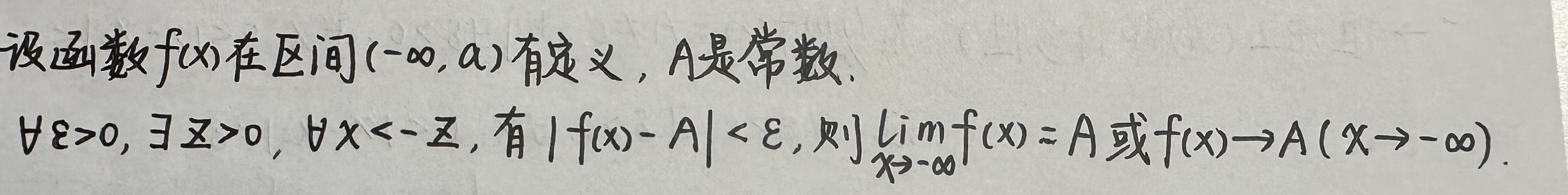
4）x趋于 x0时函数的极限：

5）x趋于x0+时函数的极限 ：

6）x趋于x0-时函数的极限：

函数极限定义的扩充（24种） ：

2、函数极限的性质（注意：对于∞这种不定号无穷大，函数极限的性质1）—4）不成立。）

1）唯一性：若函数f(x)在x0存在极限，则它的极限是唯一的。以下给出证明：

2）局部有界性：若f(x)在x0存在极限，则函数 f(x)在x0的某个去心邻域内有界。对此有两种写法，并分别给出证明：

第一种：

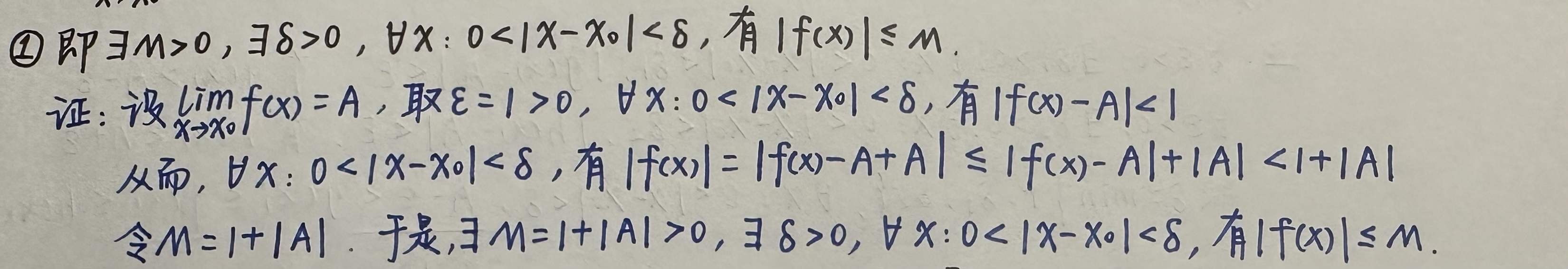
第二种：

（注：此种写法即证明方法需用到函数极限的局部保序性，下面会进行局部保序性的证明。） 

3）局部保序性：

以下给出证明：

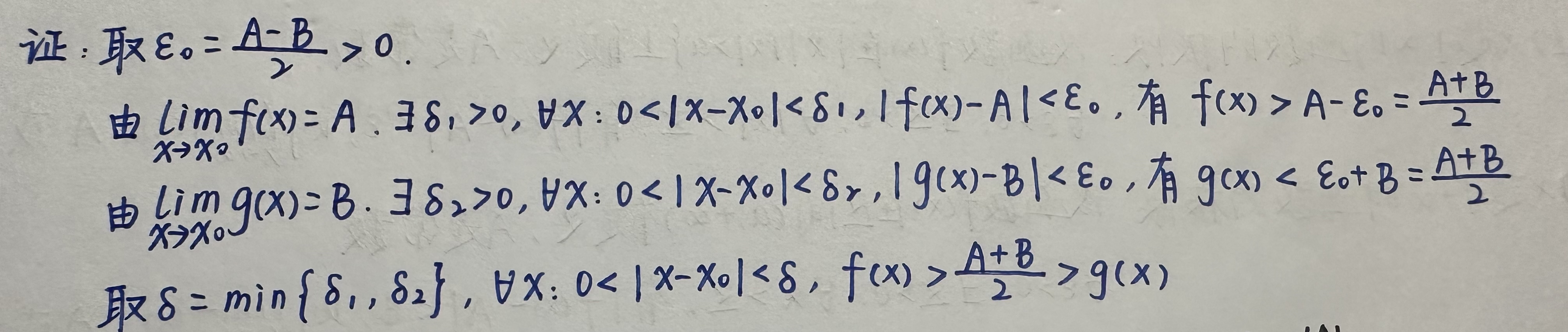
由函数极限的局部保序性，我们可以得出三个推论。以下分别是这三个推论的陈述与证明：

推论1（局部保号性）：

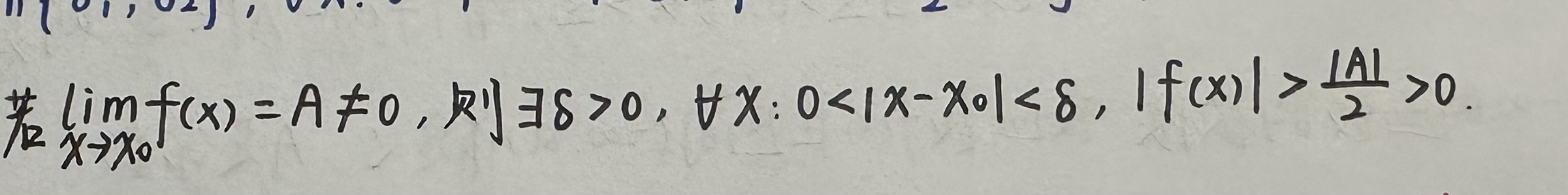
证明过程如下：（此处运用到三角形不等式，三角形不等式在后续的定理证明过程中也会经常用到，不一一说明。） 

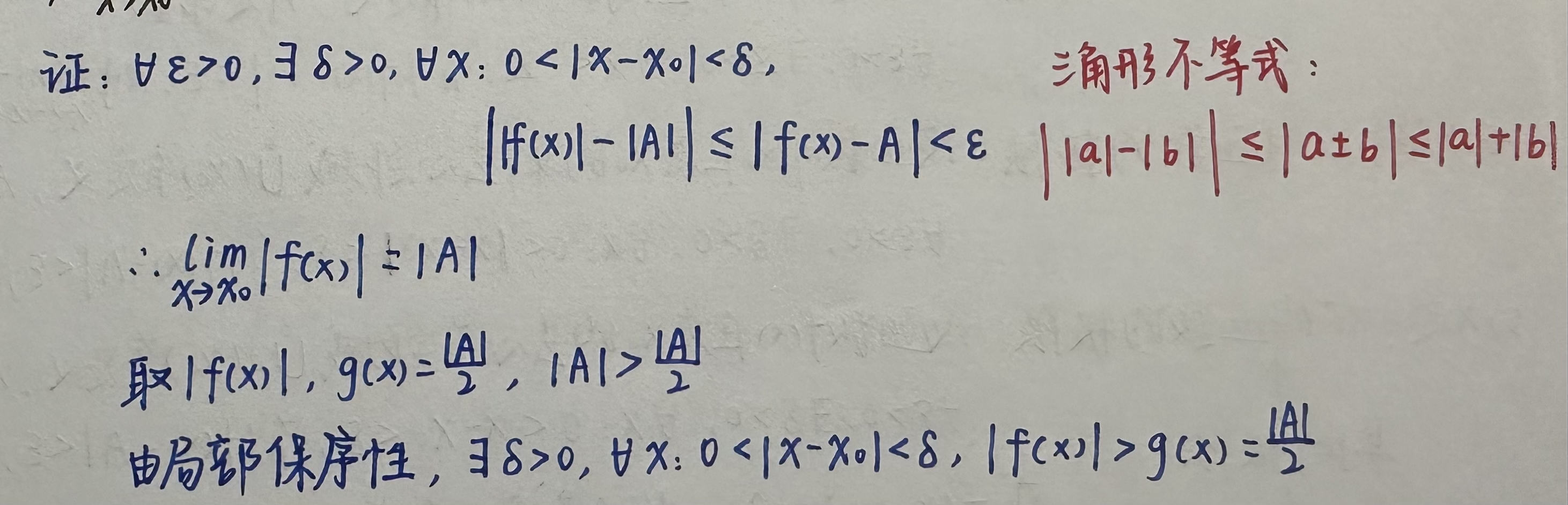
 推论2（局部保不等式性）：

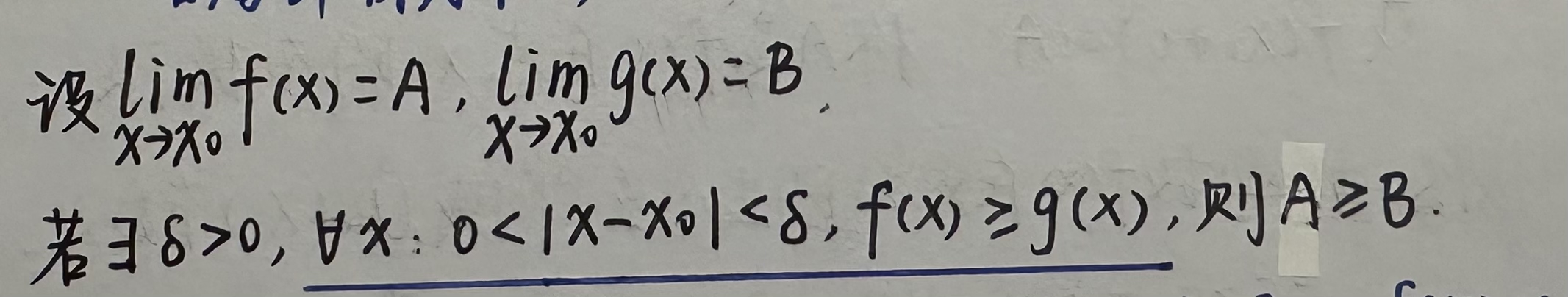
以下给出两种证明方法：

证法一：（反证法） 

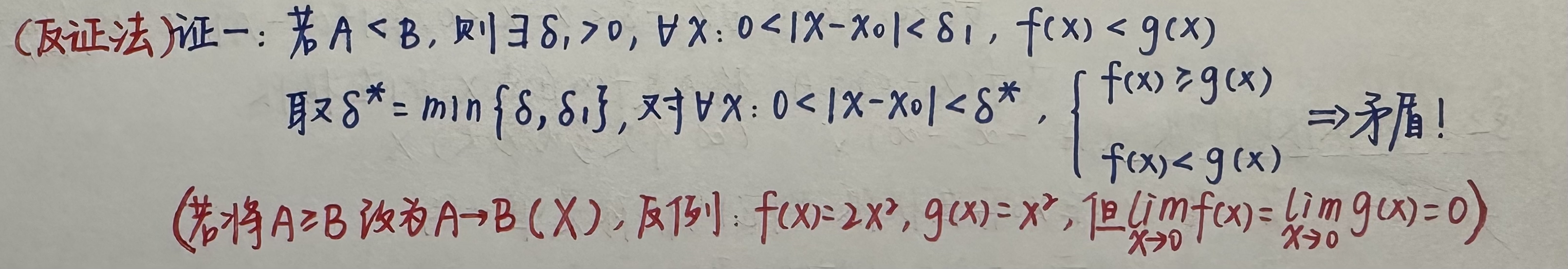
证法二：

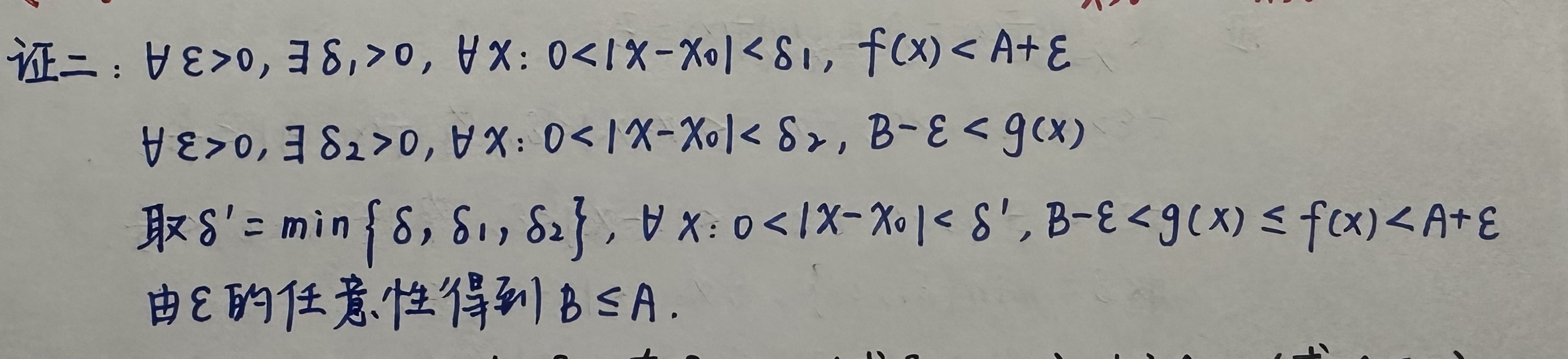
推论3：

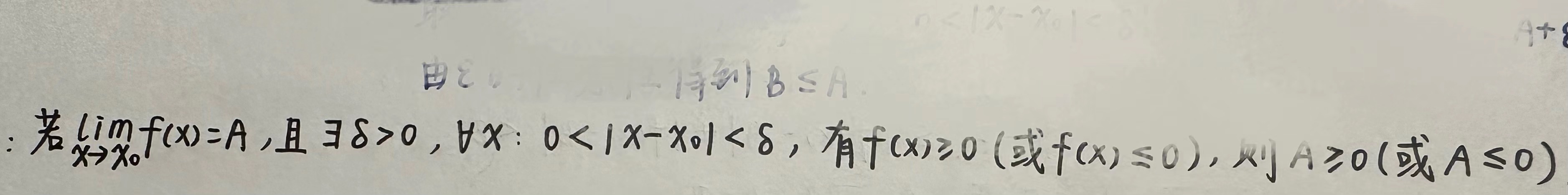
4）夹逼准则：

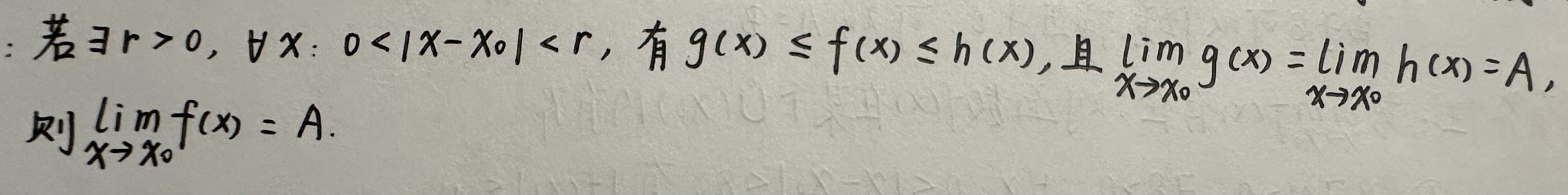
以下给出证明：

5）函数极限的四则运算：（注意：要排除待定型）

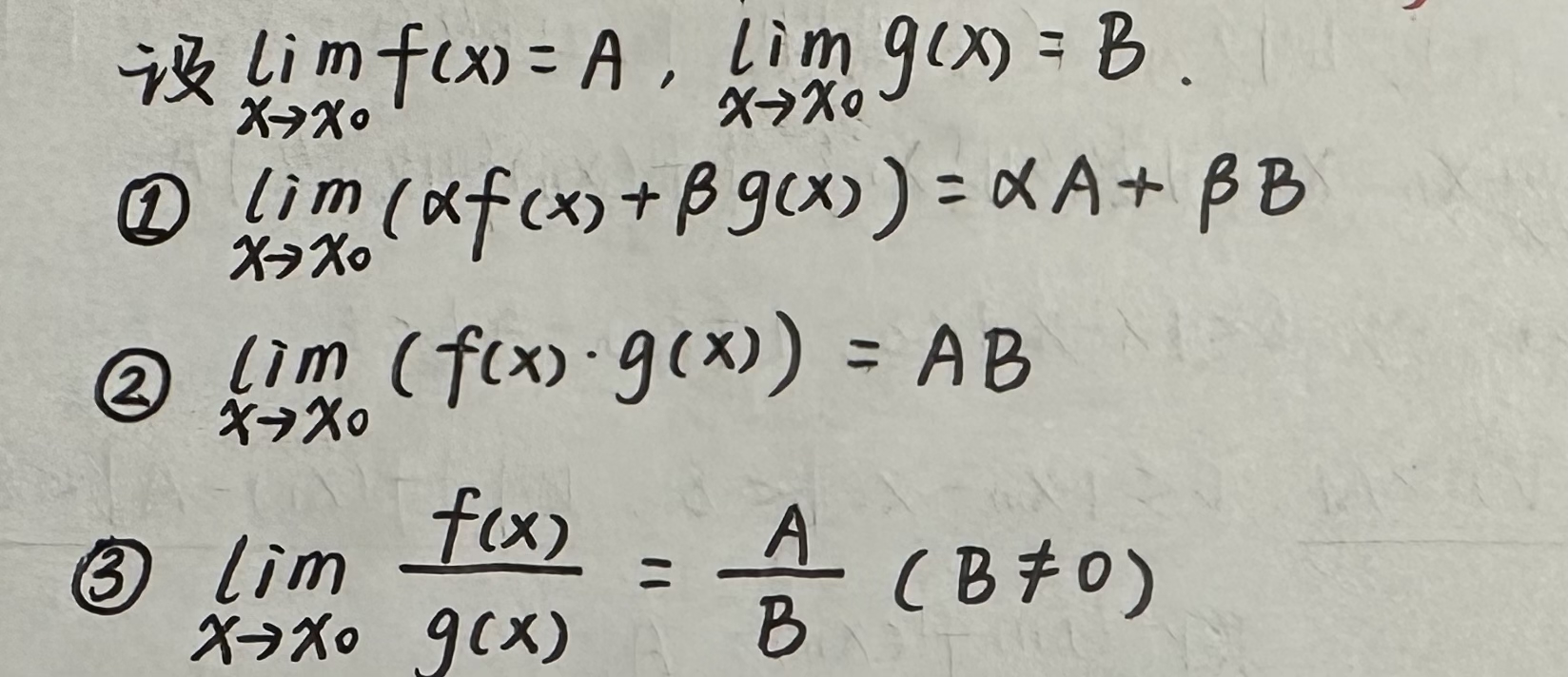
以下给出三种函数极限四则运算法则的证明过程：

6）复合函数的极限运算法则：

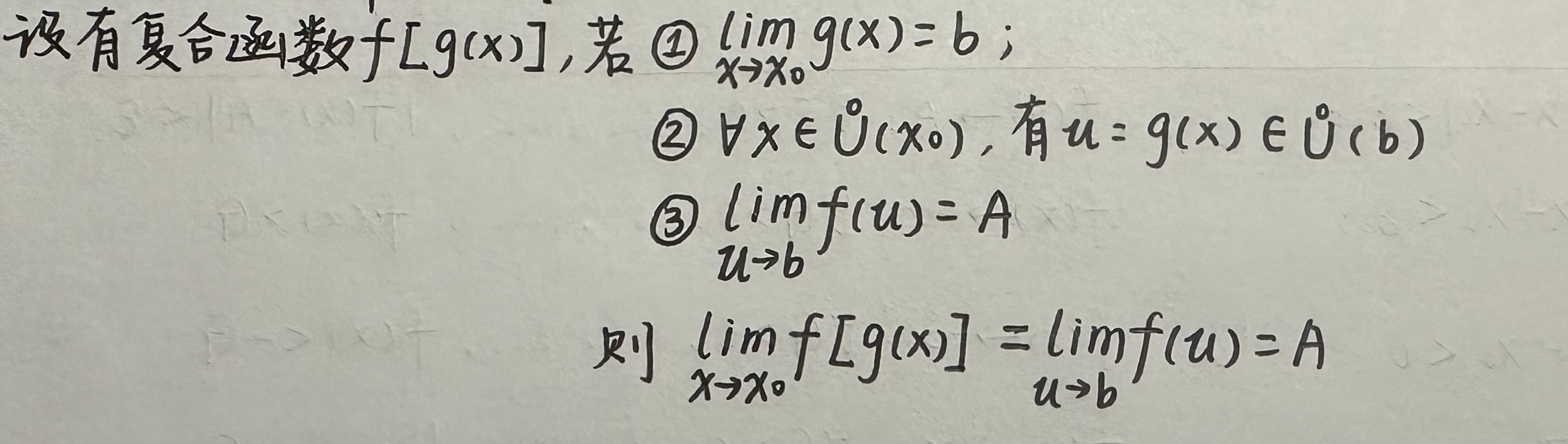
以下给出证明过程：

3、函数极限存在的条件 

 1）海涅定理（Heine定理）（此定理体现了函数极限与数列极限的关系，通常用来证明一个函数在一点没有极限。）

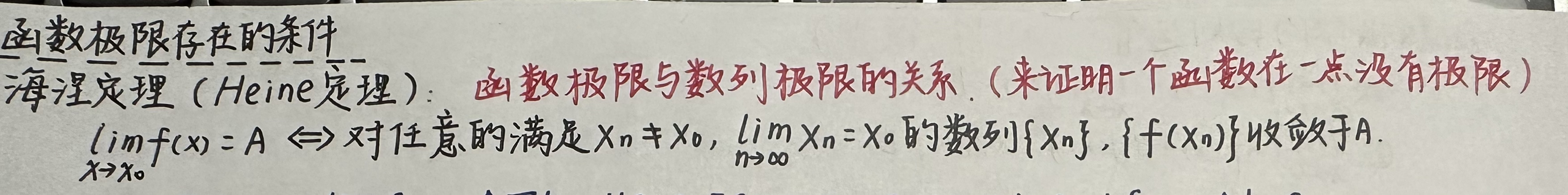
 以下给出证明：

由此可以得出两个推论，即证明一个函数在一点没有极限的两种方法：

推论1：

推论2：

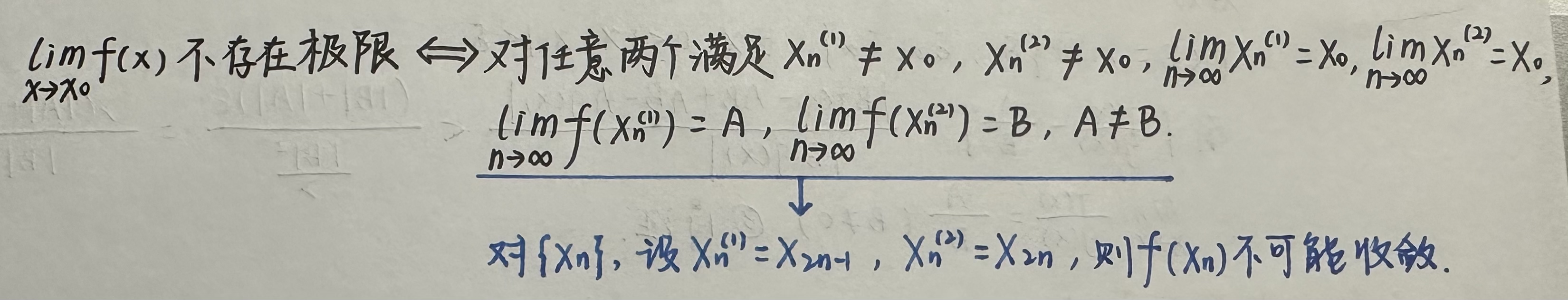
2）单调有界定理：设f(x)为定义在x0的一个去心邻域上的单调有界函数，则f(x)在x0点的有极限存在。

以下给出证明：

3）柯西收敛准则（Cauchy收敛准则）：

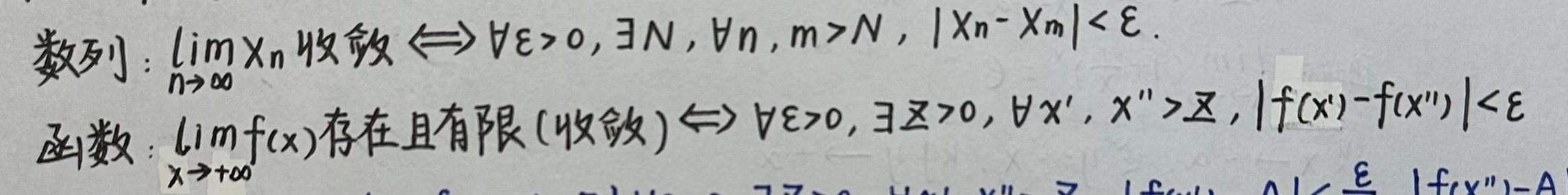
以下给出证明过程：

4、两个重要极限 

1）

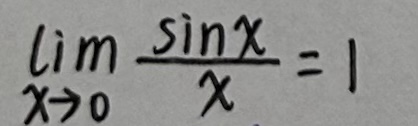
以下给出两种证明方法：

证法一：

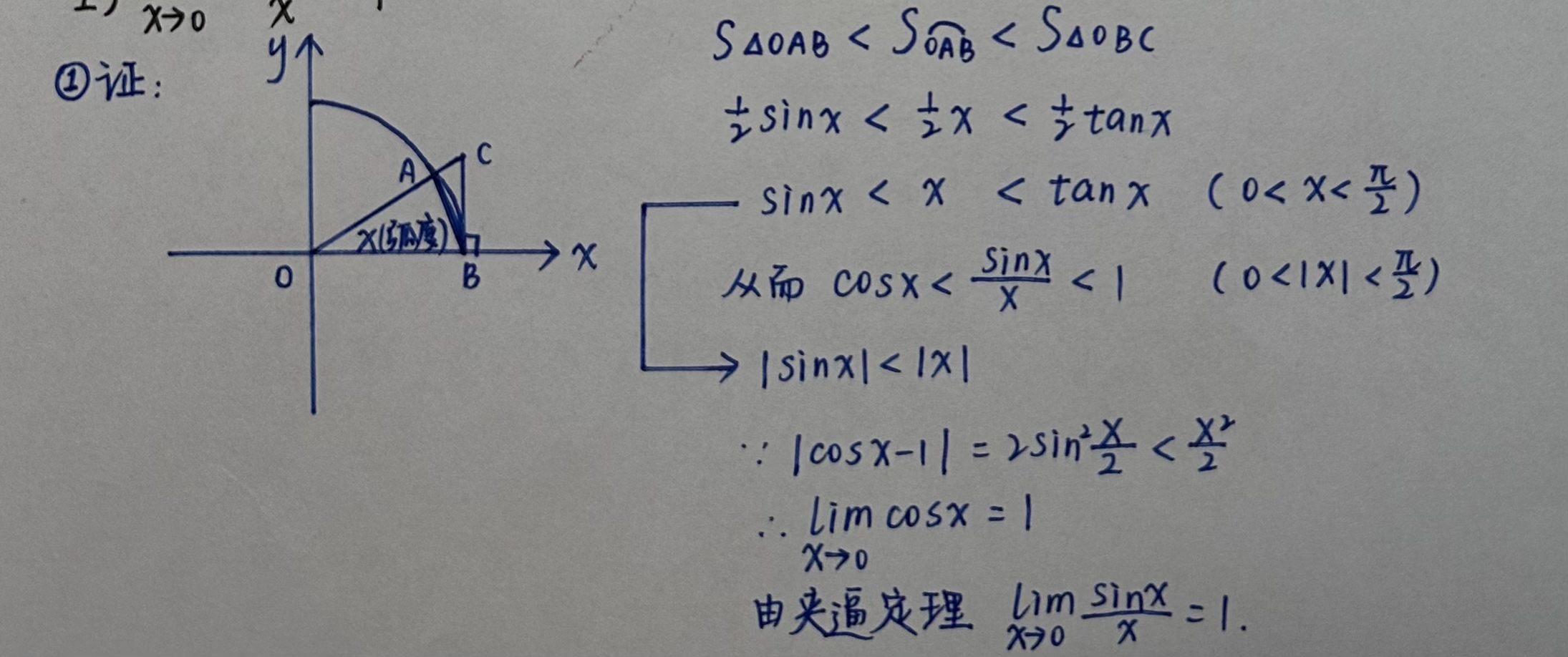
证法二：

在数列极限中，我们证明过这个式子：

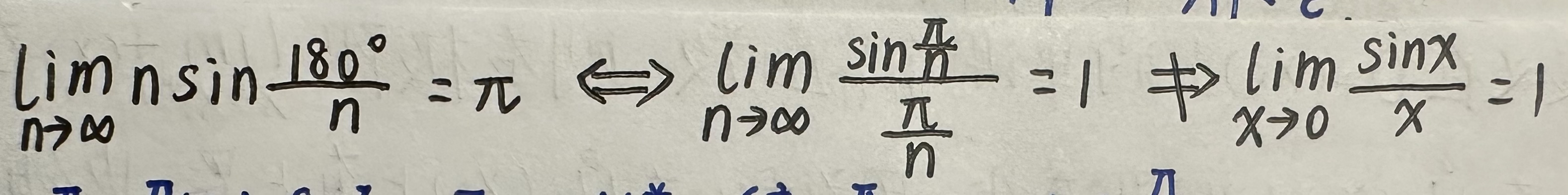
因此，我们用数列极限来进行证明：

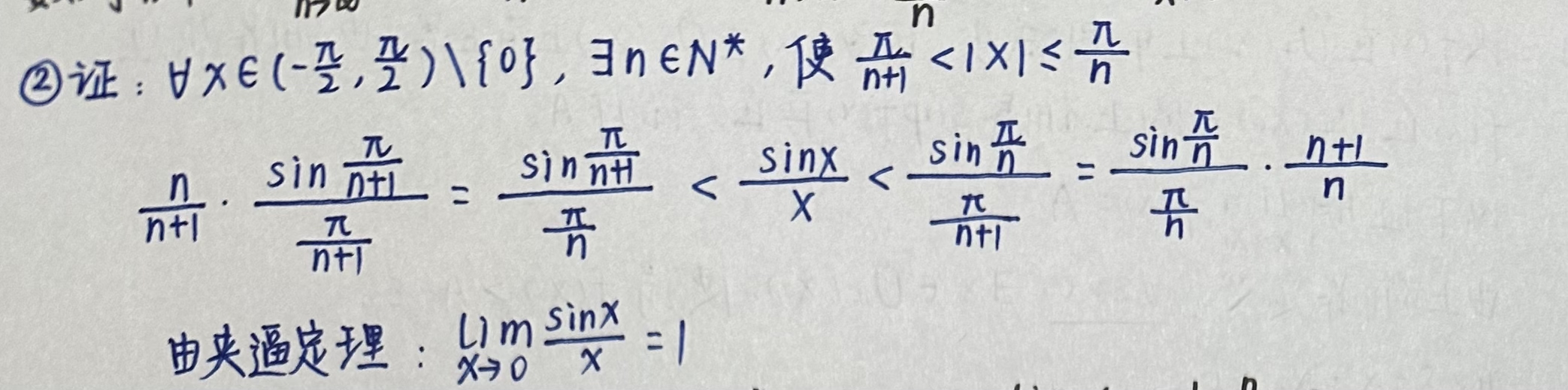
2）

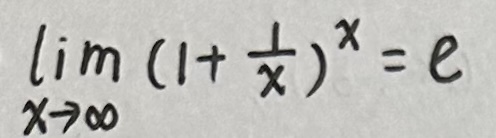
以下给出证明过程：

我们在数列极限中学过这个式子：

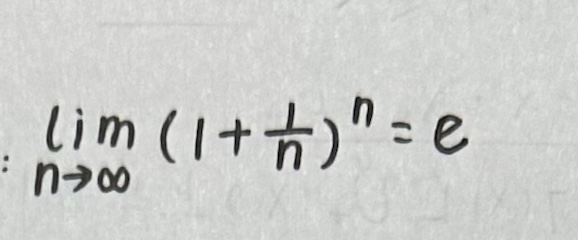
 因此，我们也用数列极限来证明：