学习设计模式——单例模式(Java语言)
高校 IT 实力排行榜 (2213)
请编写您的帖子内容
社区频道(11)
显示侧栏
卡片版式
全部
寒假里的我
MJUPC(编程挑战赛)
算法集训队
数学建模
竞赛交流
新生报道
校友交流
知识分享
求职就业
Ada助手
最新发布
最新回复
标题
阅读量
内容评分
精选

287
评分
回复

学习设计模式——单例模式(Java语言)
单例模式(Singleton Pattern) 这个类提供了一种唯一访问对象的方式,可以直接访问,不需要实例化该类的对象。 public class SingletonPatternDemo { public static void main(St
复制链接 扫一扫
分享
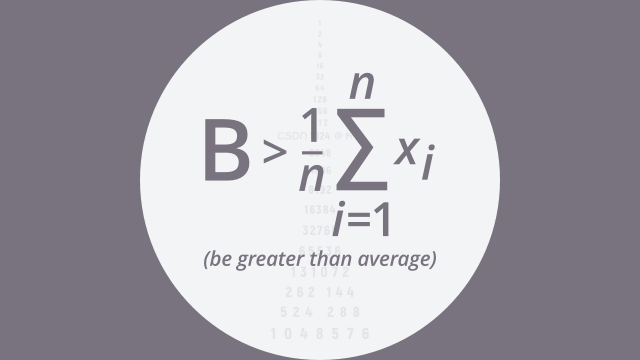
392
评分
回复

数分一致连续性和一致收敛方法
一致连续性:重点找δ 某一函数f在区间I上有定义,如果对于任意的ε>0,总有δ>0 ,使得在区间I上的任意两点x'和x",当满足|x'-x"|<δ时,|f (x')-f (x")|<ε恒成立,则该函数在区间I上一致连续 不一致连续:重点找x',x"
复制链接 扫一扫
分享

814
评分
回复

JDBC数据库连接池与DBUtils工具
目录 1.JDBC 1.1 JDBC基础 1.1.1 什么是JDBC 1.2JDBC的常用API 1.2.1Driver接口 1.2.2 DriverManager接口 1.2.3Connection接口 1.2.4 Statement接口 1.2.
复制链接 扫一扫
分享

300
评分
回复

软件测试的Selenium基础知识
一、环境搭建(以java为例) 1.下载chrome浏览器 https://www.google.cn/intl/zh-CN/chrome/ 2.查看chrome浏览器版本 设置+关于chrome 3.下载chrome浏览器驱动 下载浏览器对应版本的
复制链接 扫一扫
分享
777
评分
回复

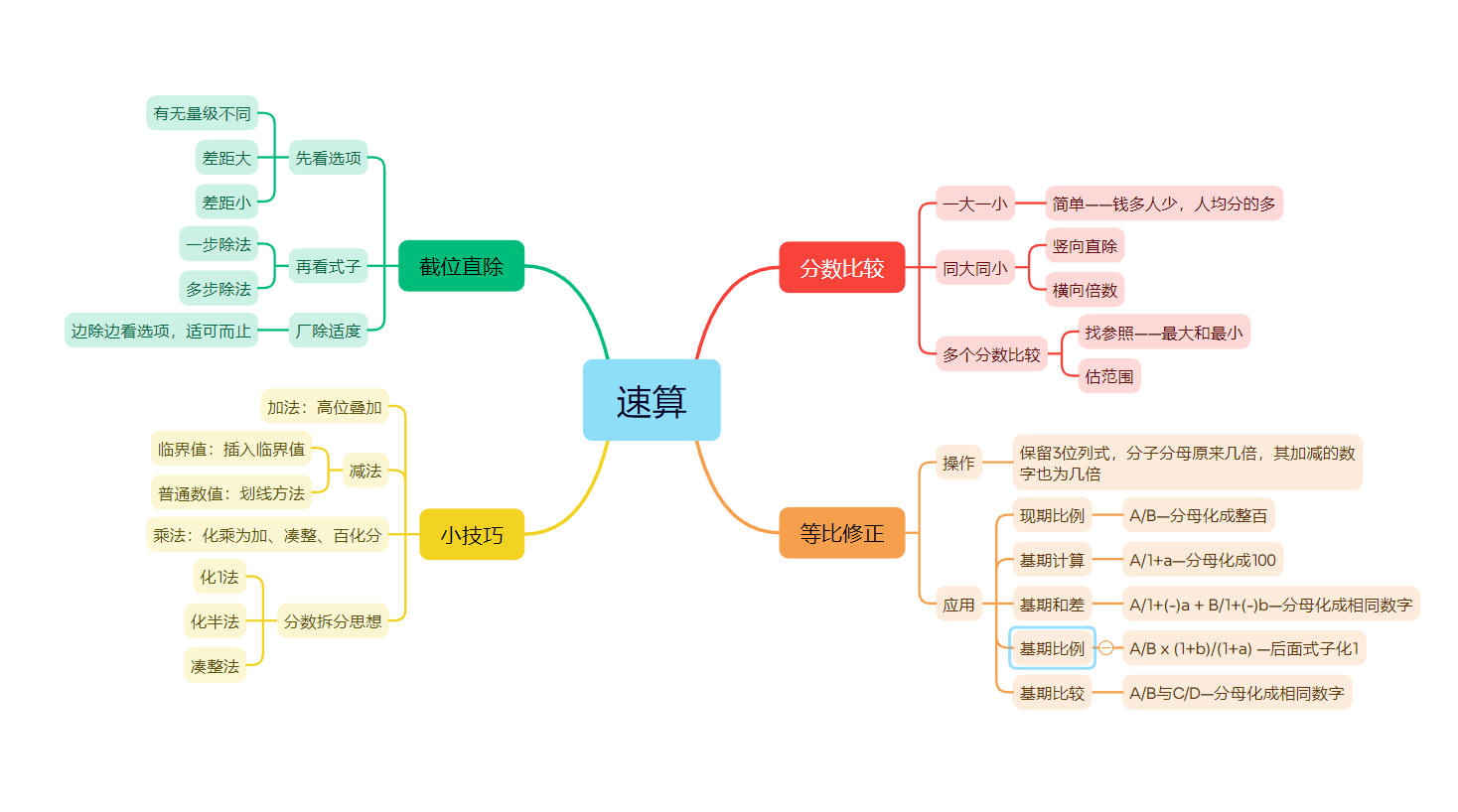
公务员考试-资料分析笔记(速算、基期量、现期量、增长率等)
目录 1.1速算 1.2基期量 1.3现期量 1.4增长率 1.2基期量 判定:求过去某个时间量 公式:基期量=现期量-增长量=现期量/1+r 考法一、基期计算 (1)加减计算 (2)除法:r>0,r<0 (3)化除为乘不可用: 选项首位
复制链接 扫一扫
分享

332
评分
回复

数学分析学习笔记分享
数学分析 一、函数单调性: 1.单调区间的讨论:(1)定义域 (2)求f’(x) (3)令f’(x)=0求驻点、求f’(x)不存在的点 (4)列表 2.利用单调性证明不等式:若f(x)在开区间(a,b)上(严格)单调增加(减少),且在点a右连续,则f
复制链接 扫一扫
分享
519
评分
回复

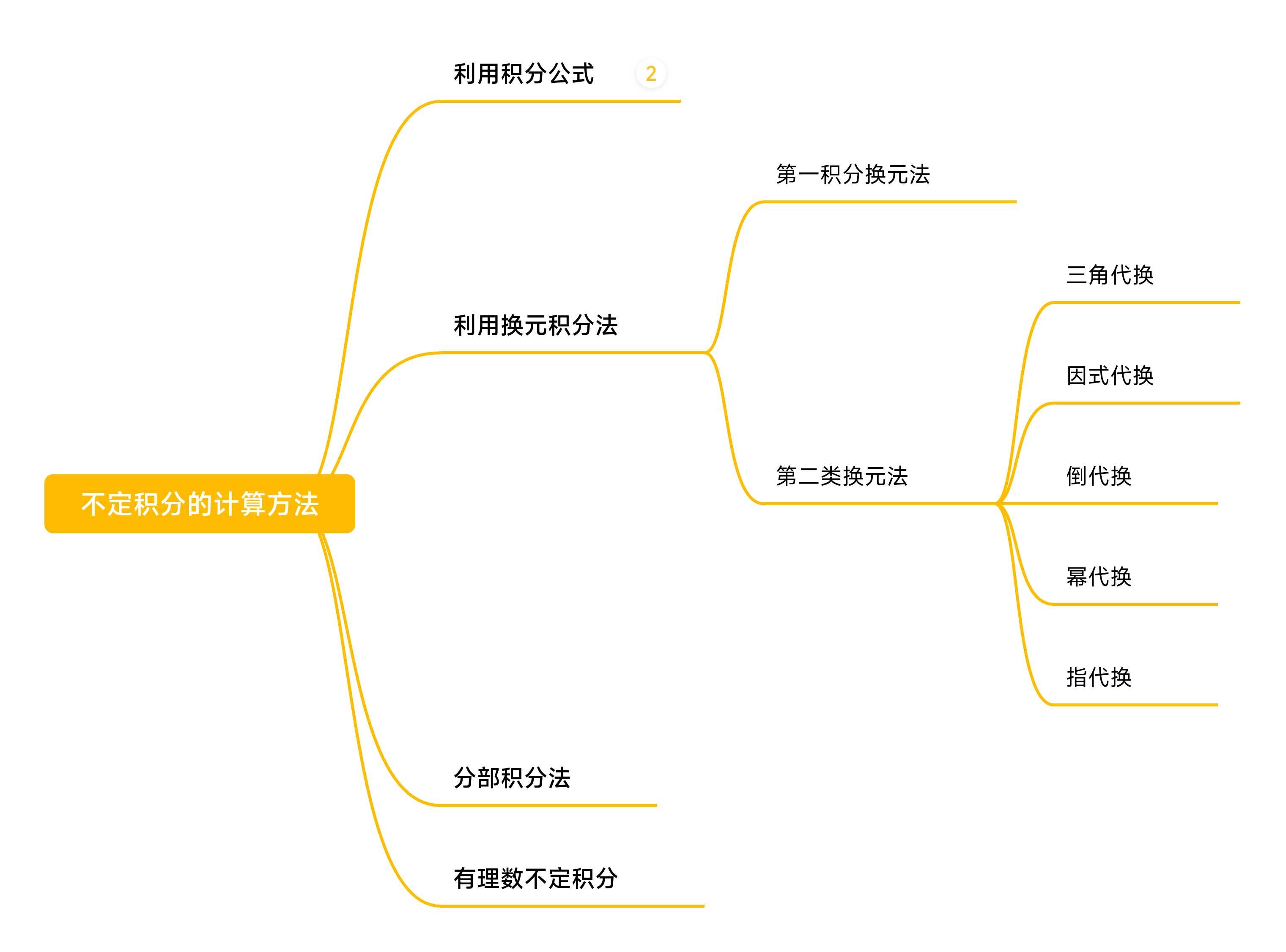
关于不定积分的计算方法
在微分学中,不定积分是定积分、二重积分等的基础,学好不定积分十分重要。然而在学习过程中发现不定积分不像微分那样直观和“有章可循”。故本文是对不定积分解题方法的归纳和总结。 不定积分看似形式多样,变幻莫测,但并不是毫无解题规律可言。本文所总结的是一般规
复制链接 扫一扫
分享

532
评分
回复

红旗永飘扬,红星永照耀——《红星照耀中国》读后感
内容简介 《红星照耀中国》是一部文笔优美的纪实性很强的报道性作品。本书真实记录了斯诺自1936年6月至10月在中国西北革命根据地进行实地采访的所见所闻,向全世界报道了中国和中国工农红军以及许多红军领袖、红军将领的情况。 全书共12篇内容描述了关于红军
复制链接 扫一扫
分享

308
评分
回复

线性规划 及 单纯形法
线性规划及单纯形法 一、一般线性规划问题的数学模型 ①一般线性规划问题的数学模型可表示为一下几种形式: s.t. 用向量形式表达时,上述模型可写为: max(或min)z=CX s.t. 式中C=(c1,c2,…,cn),X=,=,b= 用矩阵形式
复制链接 扫一扫
分享

390
评分
回复

数学分析之求数列极限的方法
简要介绍: 数学分析又称高级微积分,分析学中最古老、最基本的分支。一般指以微积分学和无穷级数一般理论为主要内容,并包括它们的理论基础(实数、函数和极限的基本理论)的一个较为完整的数学学科。而数列的极限问题是我们学习的一个比较重要的部分,同时,极
复制链接 扫一扫
分享
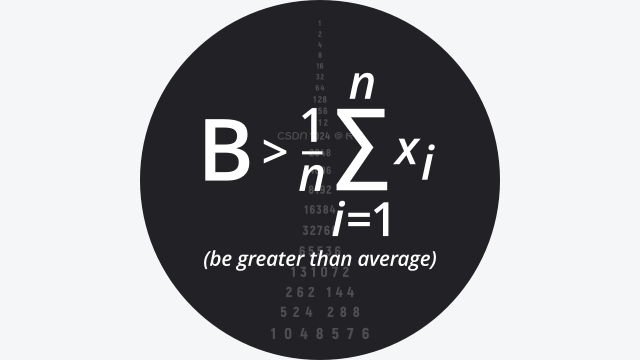
282
评分
回复

我的读书感悟之《红岩》
《红岩》读后感悟 读完《红岩》这部震撼人心的作品,我的内心久久不能平静。这部作品以解放战争时期的重庆为背景,通过细腻而真实的笔触,为我们展现了一群革命者在狱中坚持斗争、不屈不挠的奋斗精神。 书中,许云峰、江姐、成岗等革命者形象栩栩如生,他们面对敌人的
复制链接 扫一扫
分享

346
评分
回复

图论与网络分析问题(1)
图的基本概念 图 图 (graph)是一个二元组其中V(G)是非空集,称为点集 (vertex set),对于V中的每个元素,我们称其为顶点 (vertex)或节点 (node),简称点;E(G)为V(G)各结点之间边的集合,称为边集 (edge s
复制链接 扫一扫
分享

读书笔记——《星火燎原》
《星火燎原》读后感
...全文
331
评分
回复

读书笔记——《星火燎原》
《星火燎原》读后感
复制链接 扫一扫
分享

420
评分
回复

两分钟掌握web知识点(一部分)
目录 了解部分: 基础部分: 1. 文档结构标签 2. 标题标签 3. 段落和换行标签 4. 文本格式化标签 5. 链接标签 6. 列表标签 7. 图像标签 8. 表格标签 9. 表单标签 10.其他常用标签 提高部分:①margin-left: a
复制链接 扫一扫
分享

410
评分
回复

Python爬虫从0-1
Python爬虫从0-1主要讲解一些基本爬虫的使用,以及一些实战项目的编写
复制链接 扫一扫
分享

323
评分
回复

WEB攻防-通用漏洞-文件包含
一、什么是文件包含 文件包含简单来说就是引用文件。有些代码段经常能够被用到,为了避免重复敲写这一代码段, 则就将这一代码段单独放入到一个文件中,需要用时就调用出来。例如在PHP中就是利用 include进行引用(而include能够将任意种类文件(
复制链接 扫一扫
分享

332
评分
回复

《红星照耀中国》读后感
《红星照耀中国》真实记录了埃德加·斯诺自1936年6月至1936年10月在中国西北革命根据地进行实地采访的所见所闻,报道了中国和中国工农红军以及许多红军领袖、红军将领的情况。该作品从多个方面展示中国共产党为民族解放而艰苦奋斗和牺牲奉献的精神,瓦
复制链接 扫一扫
分享

366
评分
回复

F5检测远端UDP端口是否正常
使用F5内置命令:nc(NetCat) NetCat,在网络工具中有“瑞士军刀”美誉,功能非常强大,测试udp只是其中的一个功能变通。在安全领域nc常用来端口监听转发,用的比较多的也是windows版的NC,在运维中需要常用到linux上的nc,而一
复制链接 扫一扫
分享
为您搜索到以下结果:





