数学分析课堂笔记分享

[呃呃呃596]

目录
1.- 数列极限
1.1数列极限概念
1.2无穷小量、有界量、无穷大量
1.3收敛数列的性质
1.4数列极限存在的条件
1.5实数的完备性

2.- 函数的极限
2.1函数极限的概念
2.2函数极限的性质
2.3函数极限存在的条件

1.- 数列极限

1.1数列极限概念

设 {Xn} 为实数列，a 为定数.若对任给的正数 ε，总存在正整数N，使得当 n>N 时有∣Xn-a∣<ε 则称数列{Xn} 收敛于a，定数 a称为数列 {Xn} 的极限。若数列 {Xn} 没有极限，则称 {Xn} 不收敛，或称 {Xn} 为发散数列

1.2无穷小量、有界量、无穷大量

一个数列{Xn}，若既有上界又有下界，则称之为有界数列。也称数列{Xn}是一个有界量。
其中又有无穷小量和无穷大量

1.3收敛数列的性质

收敛数列有唯一性、有界性、保序性、保号性

同时还具备了夹逼定理

证明:因为limYn=a，limZn=a，所以根据数列极限的定义，对于任意给定的正数ε，存在正整数N1、N2，当n>N1时 ，有〡Yn-a∣<ε，当n>N2时，有∣Zn-a∣<ε，现在取N=max{No，N1，N2}，则当n>N时，∣Yn-a∣<ε、∣Zn-a∣<ε同时成立，且Yn≤Xn≤Zn，即a-ε<Yn<a+ε，a-ε<Zn<a+ε，又因为 a-ε<Yn≤Xn≤Zn<a+ε，即∣Xn-a∣<ε成立。也就是说
limXn=a

1.4数列极限存在的条件

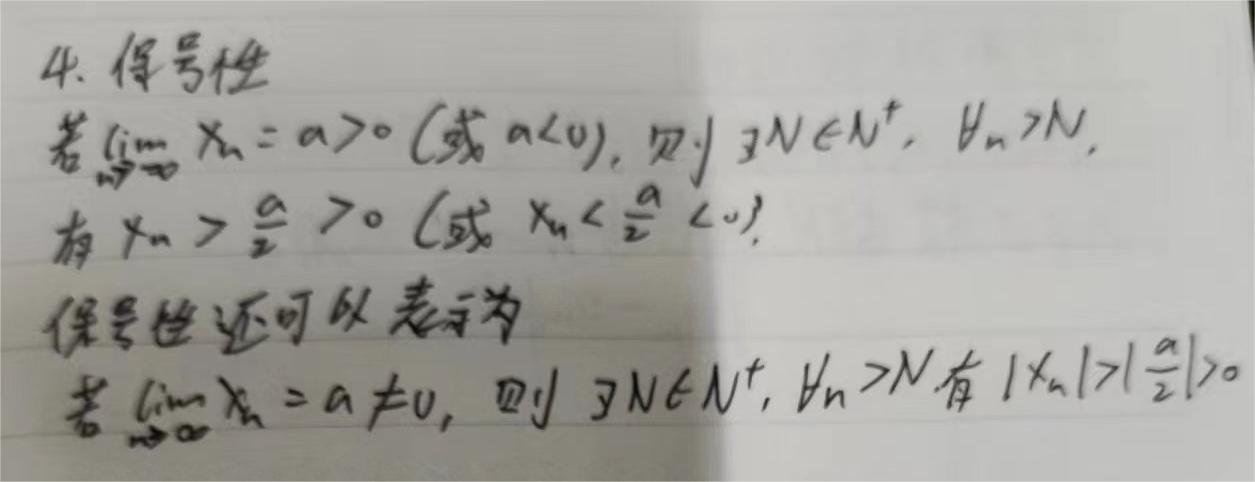
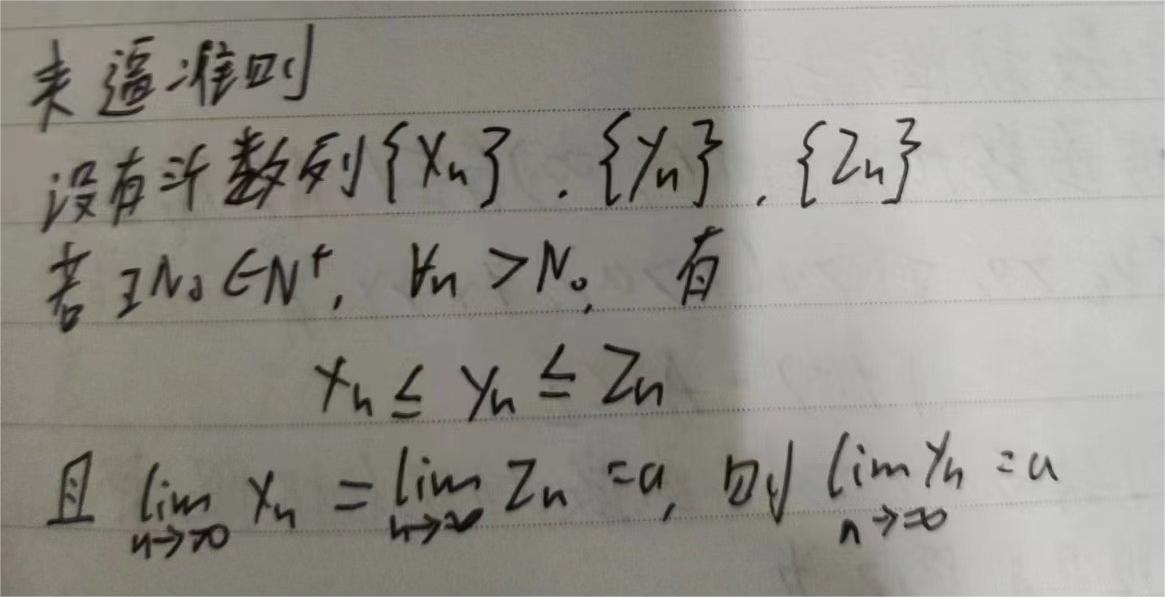
单调有界定理：若数列单调递增有上界，或单调递减有下界，则数列必存在极限。
致密性定理：有界数列必含有收敛子列。

1.5实数的完备性

柯西收敛准则的有点在于它无需借助数列以外的任何数a，只要根据数列本身的特征就可以鉴别其敛散性。
形象地说，收敛数列的各项越到后面越是“挤”在一起，这就是收敛数列最本质的特征。

2.- 函数的极限

2.1函数极限的概念

设函数y=f（x）在点X0的某个去心领域中有定义，即存在ρ>0，使O（X0，ρ）{X0}。

如果存在实数A，对于任意给定的ε>0，可以找到δ>0，使得当0<|x-x0|<δ时，成立│f(x)-A│<ε ,

则称数A为函数f(x)当x→+∞时的极限，记作 f(x)→A(x→+∞).

2.2函数极限的性质

函数极限存在唯一性、局部有界性、局部保序性

2.3函数极限存在的条件

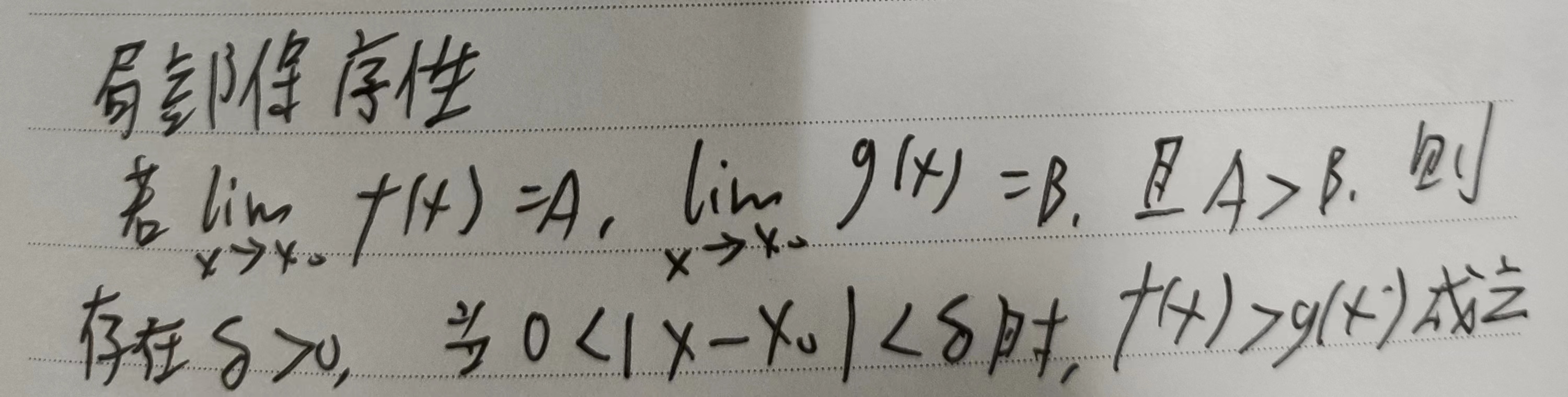
海涅定理

单调有界准则：单调增加（减少）有上（下)界的数列必定收敛。
柯西准则：数列收敛的充分必要条件是任给ε>0,存在N(ε),使得当n>N,m>N时，都有|am-an|<ε成立。