高等代数之行列式章节笔记

[Yzc0102]

目录

1.行列式的定义

2.行列式的性质与计算

3.行列式按一行（列）展开

4.拉普拉斯定理

5.克拉默法则

1.行列式的定义

1.1基本概念

行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det(A)或 | A | 。无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用。
 

例题： 

---

 

 1.2排列及其逆序数

1.排列：

 2.逆序：

 3.逆序数：

4.奇偶排列 

5.对换： 

  1.3n阶行列式(注意：各项符号由列标排列与行标排列的逆序数和决定即奇负偶正)

 2.行列式的性质与计算

  2.1行列式的性质

   有如下5条及推论： 

 2.2行列式的计算

 上述性质2,3,5介绍了行列式关于行和关于列的三种运算，即ri←→rj,kri,ri＋krj,以及ci←→cj,kci,ci+kcj利用这些运算可简化行列式的计算，特别是利用运算ri＋krj（或ci+kcj)，可以把行列式中许多元素化为零，进而把行列式化为三角形行列式，最后得到行列式的值．

下面给出一个例题：

解法如下： 

 接着给出几种特殊行列式计算：

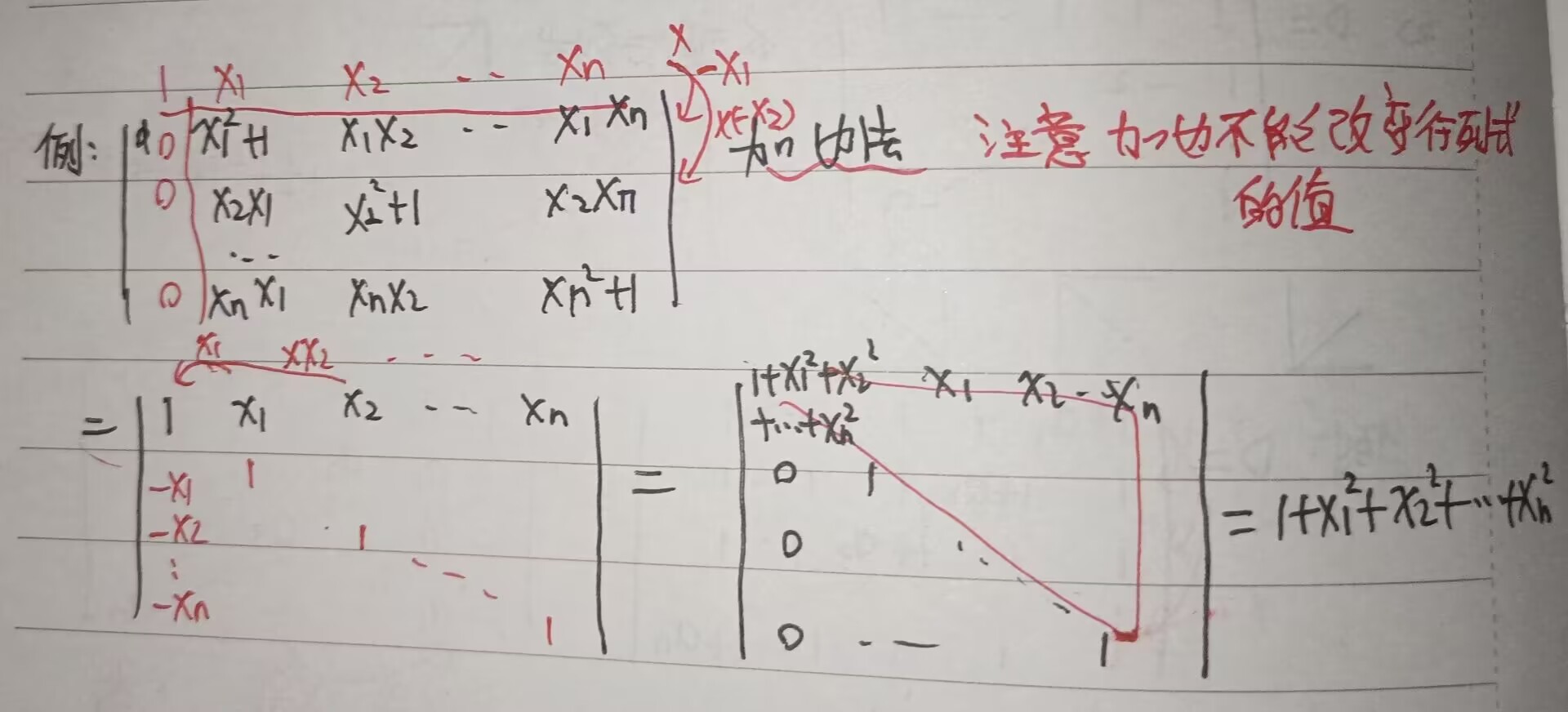
1.爪形行列式：

 2.范德蒙德行列式：

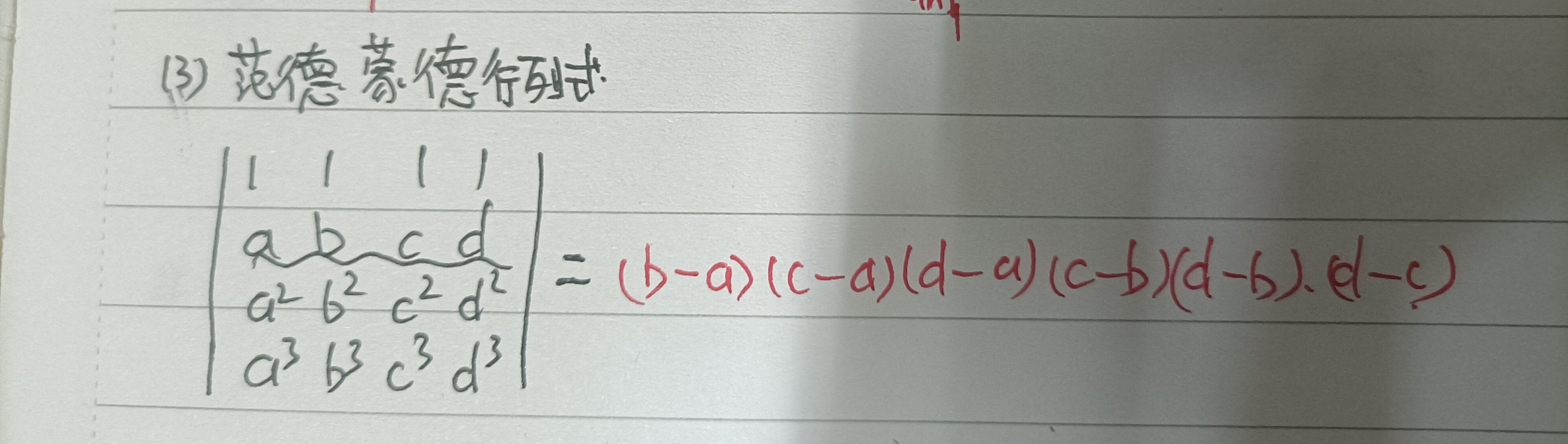
 补充：加边法

例题如下：

 3.行列式按一行（列）展开

行列式按一行（列）展开可以将高阶行列式转化为低阶行列式，进而简便计算，为此先引进余子式与代数余子式

3.1余子式与代数余子式

定义：在n阶行列式中，把元素aₒₑi所在的第o行和第e列划去后，留下来的n-1阶行列式叫做元素aₒₑi的余子式，记作Mₒₑ，将余子式Mₒₑ再乘以-1的o+e次幂记为Aₒₑ，Aₒₑ叫做元素aₒₑ的代数余子式。具体如下：

 3.2行列式按一行（列）展开定理

定理：

 例如：

 4.拉普拉斯定理

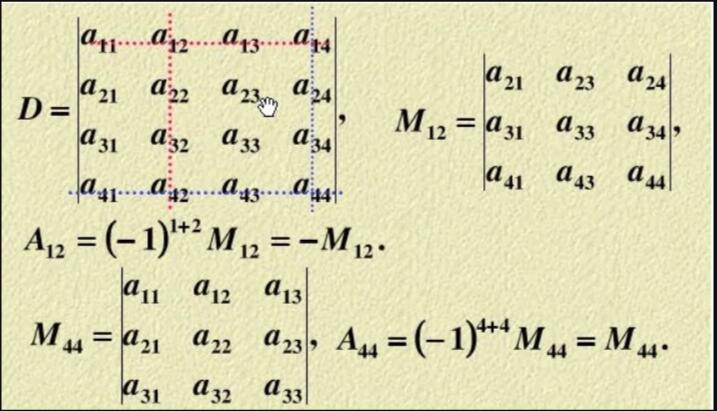
定理：在n阶行列式D=|aij| 中，任意取定k行（列），1≤k≤n-1，由这k行（列）的元素所构成的一切k阶子式与其代数余子式的乘积的和等于行列式D的值。

 例

 5.克拉默法则

定理：n元齐次线性方程组有非零解的充要条件是其系数行列式为零。等价地，方程组有唯一的零解的充要条件是系数矩阵的行列式不为零，其矩阵可逆

 例题