C语言 最小生成树 （Kruskal算法和Prim算法）

微软技术分享 微软全球最有价值专家
优质创作者: 编程框架技术领域
领域专家: 操作系统技术领域
2024-01-30 09:13:12

前言

在一个加权连通图中，最小生成树（Minimum Spanning Tree，简称MST）就是连接所有节点的一棵树，并且使得树上边的总权值最小。这个树又被称为图的“最小权重生成树”。

最小生成树问题是一个重要的组合优化问题，在很多现实应用中都有广泛的应用，比如网络规划、电力工程设计、交通运输等领域。

最小生成树问题可以通过解决环路问题来得到解决。如果移除加权连通图中所有环路，那么剩下的就是一棵最小生成树。由于最小生成树只包含 n-1 条边，因此也是可行运输树的一种特殊形式。

求解最小生成树问题的经典算法包括普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。

视频讲解-----> 

最小生成树 Prim算法和Kruskal算法

 

普里姆算法

Prim算法是基于贪心策略的算法，其基本思想是以一个点为起点开始，每次选择一条与当前生成树相邻的最短边，将其加入生成树中，直到所有点都被加入生成树为止。

基本流程：

  • 定义辅助数组dist（各顶点离当前生成树距离）、visited（标记顶点是否加入生成树）、parent（生成树中每个节点的父节点）。
  • 将各顶点到生成树的距离设为正无穷大，表示暂时无法到达。置起点u的dist[u]为0。
  • 找到离当前生成树最近的顶点t,将其加入生成树并标记。
  • 更新顶点t未被标记的邻接点离当前生成树的距离，并更新其父节点。
  • 重复步骤3和4，直到所有点都被加入生成树为止。
  • 打印最小生成树以及权值和。

需要注意的是，如果原图不连通，则最终生成的树只是原图的一个连通分量的最小生成树，需要对每个连通分量分别进行求解。

无向网G以邻接矩阵形式储存，从顶点u出发构造最小生成树。

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MVNum 100//最大顶点数
#define MaxInt 66666//表示极大值
typedef struct {
    char vexs[MVNum];//顶点表（顶点为字符型）
    int arcs[MVNum][MVNum];//邻接矩阵（权值为整型）
    int vexnum, arcnum;//图的当前点数和边数
}AMGraph;

//定位
int LocateVex(AMGraph* G, char v) {
    int i;
    for (i = 0; i < G->vexnum; i++) {
        if (G->vexs[i] == v) {
            return i;
        }
    }
    return -1;
}
//创建无向网G
AMGraph* CreateUDN() {
    int i, j, k, w;
    char v1, v2;
    AMGraph* G = malloc(sizeof(AMGraph));
    printf("输入总顶点数，边数\n");
    scanf("%d%d", &G->vexnum, &G->arcnum);
    getchar();//吸收换行符
    printf("依次输入点的信息\n");
    for (i = 0; i < G->vexnum; i++) {
        scanf("%c", &G->vexs[i]);
    }
    getchar();//吸收换行符
    for (i = 0; i < G->vexnum; i++)
        for (j = 0; j < G->vexnum; j++) {
            if (i == j) {
                G->arcs[i][j] = 0;
            }
            else {
                G->arcs[i][j] = MaxInt;
            }
        }
    for (k = 0; k < G->arcnum; k++) {
        printf("输入一条边依附的顶点及权值\n");
        scanf("%c%c", &v1, &v2);
        scanf("%d", &w);
        getchar();//吸收换行符
        i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在顶点数组的下标
        G->arcs[i][j] = w;//边<v1,v2>权值置为w
        G->arcs[j][i] = w;//无向网对称边<v2,v2>权值也置为w
    }
    return G;
}

//普里姆算法
void Prim(AMGraph* G, int u) {
    //u为起点
    int dist[MVNum];//储存各顶点离集合U的距离
    bool visited[MVNum];//标记顶点是否加入生成树
    int parent[MVNum];//生成树中每个节点对应的父节点
    int i, j, k, t, min_dis;
    //初始化
    for (i = 0; i < G->vexnum; i++) {
        dist[i] = MaxInt;
        visited[i] = false;
    }
    dist[u] = 0;
    parent[u] = -1;
    for (i = 1; i < G->vexnum; i++) {
        t = -1;
        min_dis = MaxInt;
        //找到离当前生成树最近的顶点t。
        for (j = 0; j < G->vexnum; j++) {
            if (!visited[j] && dist[j] < min_dis) {
                t = j;
                min_dis = dist[j];
            }
        }
        if (t == -1)    break;//生成树无法延伸
        visited[t] = true;//标记顶点t
        //更新顶点t未被标记的邻接点离当前生成树的距离，并更新其父节点。
        for (k = 0; k < G->vexnum; k++) {
            if (!visited[k] && G->arcs[t][k] < dist[k]) {
                dist[k] = G->arcs[t][k];
                parent[k] = t;
            }
        }
    }
    //打印最小生成树以及权值和
    printf("最小生成树：\n");
    int count = 0;
    for (i = 0; i < G->vexnum; i++) {
        if (parent[i] != -1) {
            printf("<%c,%c>  ", G->vexs[parent[i]], G->vexs[i]);
        }
        count += dist[i];
    }
    printf("\n权值和为:%d\n", count);
}

int main() {
    AMGraph* G = CreateUDN();
    Prim(G, 0);
    return 0;
}

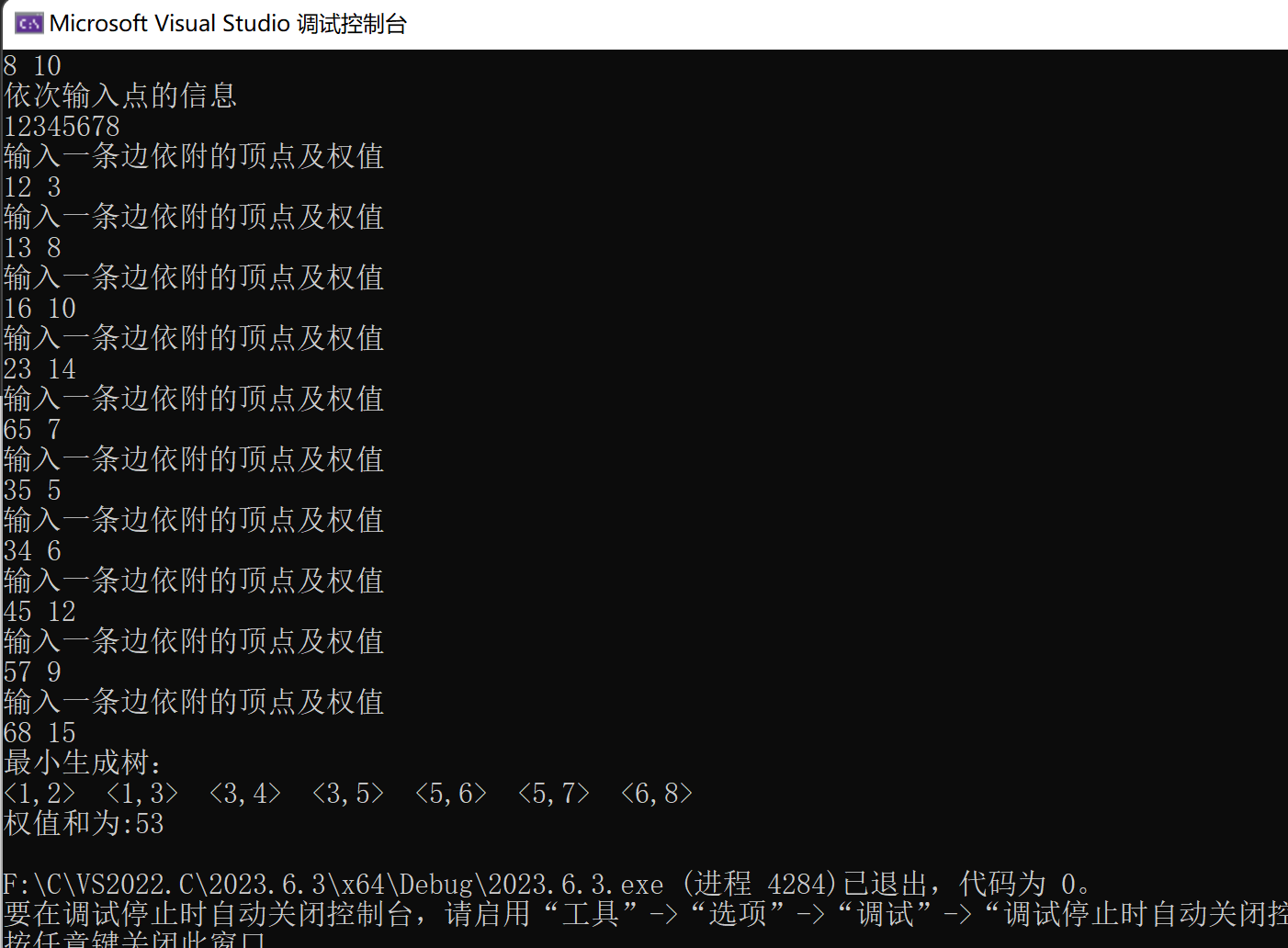
运行代码，构造下图无向网的最小生成树： 

https://img-blog.csdnimg.cn/ef7c861c77384e4c8ba70ff9da85f0d7.png

运行结果： 

https://img-blog.csdnimg.cn/f37c79ba762e49cb993f525d71980032.png

Kruskal算法

克鲁斯卡尔算法是一种基于并查集的算法。其主要思想是将所有边按照权重从小到大进行排序，依次加入边，直到连接所有点，但要确保新加入的边不会形成环。

基本流程：

  • 定义结构体数组Edges（储存边的信息）和并查集数组Vexset。
  • 调用快排函数将数组Edges中的所有边按照权重从小到大进行排序。
  • 初始化并查集Vexset，将每一个顶点都看作一个单独的集合。由于每个集合只包含一个元素，因此该元素即为该集合代表。
  • 依次选择权重最小的边，并判断该边连接的两个顶点是否属于同一个集合（可以通过并查集来实现）。如果不在同一个集合中，则合并这两个集合，更新权重和，并输出该边。
  • 输出权重和。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MVNum 100//最大顶点数
#define MaxInt 66666//表示极大值
typedef struct {
    char vexs[MVNum];//顶点表（顶点为字符型）
    int arcs[MVNum][MVNum];//邻接矩阵（权值为整型）
    int vexnum, arcnum;//图的当前点数和边数
}AMGraph;

//定位
int LocateVex(AMGraph* G, char v) {
    int i;
    for (i = 0; i < G->vexnum; i++) {
        if (G->vexs[i] == v) {
            return i;
        }
    }
    return -1;
}
//创建无向网G
AMGraph* CreateUDN() {
    int i, j, k, w;
    char v1, v2;
    AMGraph* G = malloc(sizeof(AMGraph));
    printf("输入总顶点数，边数\n");
    scanf("%d%d", &G->vexnum, &G->arcnum);
    getchar();//吸收换行符
    printf("依次输入点的信息\n");
    for (i = 0; i < G->vexnum; i++) {
        scanf("%c", &G->vexs[i]);
    }
    getchar();//吸收换行符
    for (i = 0; i < G->vexnum; i++)
        for (j = 0; j < G->vexnum; j++) {
            if (i == j) {
                G->arcs[i][j] = 0;
            }
            else {
                G->arcs[i][j] = MaxInt;
            }
        }
    for (k = 0; k < G->arcnum; k++) {
        printf("输入一条边依附的顶点及权值\n");
        scanf("%c%c", &v1, &v2);
        scanf("%d", &w);
        getchar();//吸收换行符
        i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在顶点数组的下标
        G->arcs[i][j] = w;//边<v1,v2>权值置为w
        G->arcs[j][i] = w;//无向网对称边<v2,v2>权值也置为w
    }
    return G;
}

struct Edge {
    char Head;//边的始点
    char Tail;//边的终点
    int weight;//边的权重
};

//快排函数的比较函数
int cmp(const void* a, const void* b) {
    return ((struct Edge*)a)->weight - ((struct Edge*)b)->weight;
}

//克鲁斯卡尔算法
void Kruskal(AMGraph* G) {
    struct Edge Edges[MVNum];//储存边的结构体数组
    int Vexset[MVNum];//并查集
    int i, j, k, v1, v2, vs1, vs2;
    int count = 0;//储存权重和
    //将图中所有边存入数组Edges
    for (i = 0, k = 0; i < G->vexnum; i++) {
        for (j = i + 1; j < G->vexnum; j++) {
            if (G->arcs[i][j] != 0 && G->arcs[i][j] != MaxInt) {
                Edges[k++] = (struct Edge){ G->vexs[i],G->vexs[j],G->arcs[i][j] };
            }
        }
    }
    //调用快排函数，按权重从小到大排序
    qsort(Edges, G->arcnum, sizeof(struct Edge), cmp);
    //初始化并查集
    for (i = 0; i < G->vexnum; i++) {
        Vexset[i] = i;
    }
    //遍历数组Edges中的边
    for (i = 0; i < G->arcnum; i++) {
        v1 = LocateVex(G, Edges[i].Head);//该边的始点序号
        v2 = LocateVex(G, Edges[i].Tail);//该边的终点序号
        vs1 = Vexset[v1];//vs1为顶点v1所属集合编号
        vs2 = Vexset[v2];//vs2为顶点v2所属集合编号
        //编号不相等时，说明顶点v1和v2不属于同一个集合
        if (vs1 != vs2) {
            printf("<%c,%c>  ", G->vexs[v1], G->vexs[v2]);//输出此边
            count += G->arcs[v1][v2];//更新权重和
            //合并这两个集合，即统一编号
            for (j = 0; j < G->vexnum; j++) {
                //集合编号为vs2的都改为vs1
                if (Vexset[j] == vs2) {
                    Vexset[j] = vs1;
                }
            }
        }
    }
    printf("\n权重和为%d\n", count);
}

int main() {
    AMGraph* G = CreateUDN();
    printf("最小生成树：\n");
    Kruskal(G);
    return 0;
}

运行程序，求下图最小生成树： 

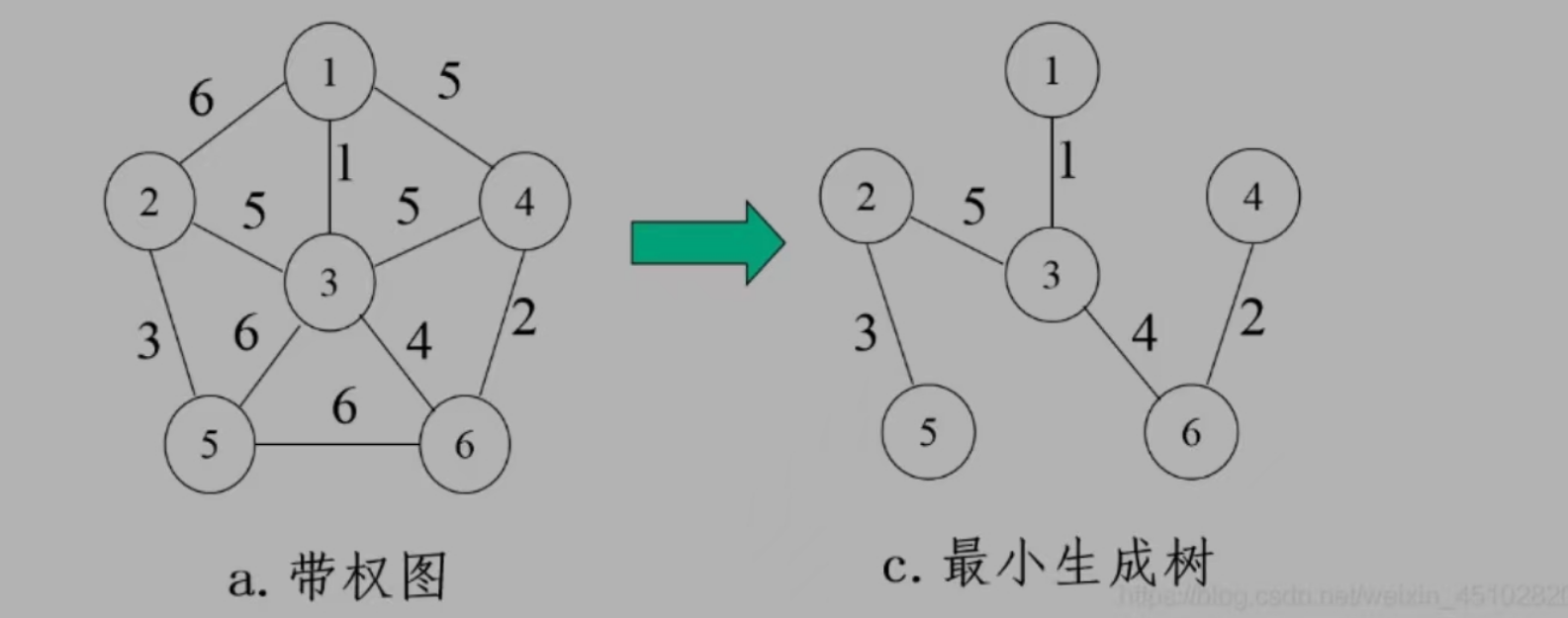
https://img-blog.csdnimg.cn/35c8f05884664a26884909738c39e917.png

 运行结果：

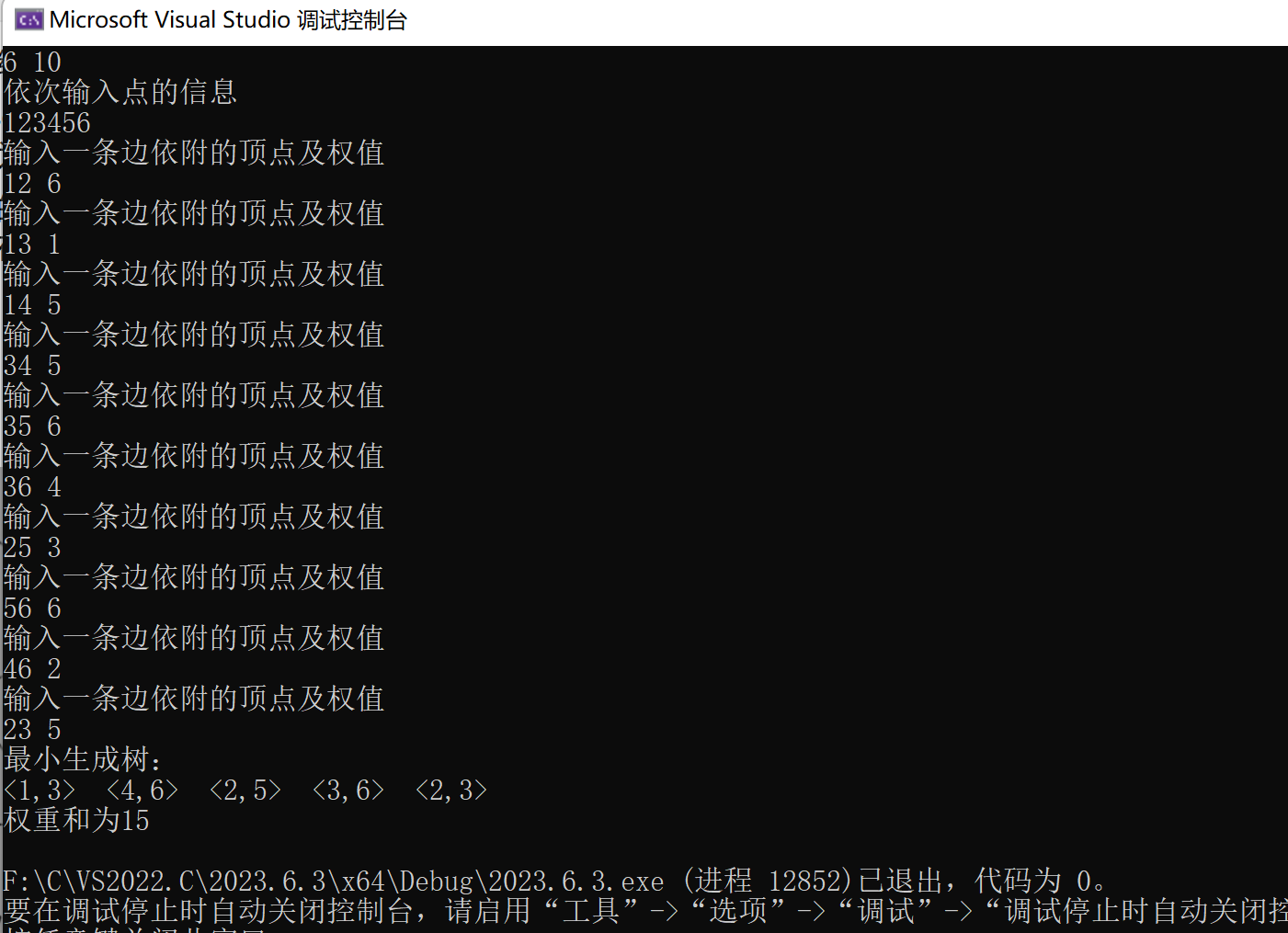
https://img-blog.csdnimg.cn/d5413e878b5740afbe9562ed49fbc821.png

总结

以上算法的实现，普里姆算法的时间复杂度为O（n^2）,与网中边上无关，因此适用于求稠密网的最小生成树；克鲁斯卡尔算法时间复杂度为O（eloge），与网中边数有关，与普里姆算法相比，更适合求稀疏网的最小生成树。

 

文章来源： https://blog.csdn.net/m0_73070900/article/details/131029333
版权声明： 本文为博主原创文章，遵循CC 4.0 BY-SA 知识共享协议，转载请附上原文出处链接和本声明。

...全文
49 回复 打赏 收藏 转发到动态 举报
写回复
用AI写文章
回复
切换为时间正序
请发表友善的回复…
发表回复
cpp-图论算法最小生成树Prim算法和Kruskal算法C实现
本文将详细介绍两种经典算法来解决最小生成树问题：Prim算法和Kruskal算法，并以C语言实现为例进行讲解。 ### Prim算法 Prim算法是一种贪心算法，其基本思想是从一个初始节点开始，逐步添加最短的边，直到连接到...
最小生成树kruskal算法并查集版 C语言实现 - Slyar Home
最小生成树kruskal算法并查集版 C语言实现 - Slyar Home
c语言实现最小生成树的prim算法和kruskal算法
详细的c语言实现最小生成树的prim算法和kruskal算法，非常有用的
最小生成树Prim算法的C语言程序
"最小生成树Prim算法的C语言程序" Prim 算法是最小生成树的一种特殊算法，它的特点是集合 A 的边总是只形成单棵树。该算法的基本思路是：任选一个顶点（本实验取①为起始点），将其涂红，其余顶点为白点；在一个...
最小生成树kru和prim算法的c语言实现
Kruskal算法是一种基于边的贪心策略来构建最小生成树。它的主要步骤如下： 1. **按权值升序排序所有边**：首先，将图中的所有边按照权重从小到大进行排序。 2. **初始化空树**：创建一个空集合，作为最终最小生成...
微软技术社区

6,120

社区成员

37,287

社区内容

发帖
与我相关
我的任务
社区描述
微软技术社区为中国的开发者们提供一个技术干货传播平台，传递微软全球的技术和产品最新动态，分享各大技术方向的学习资源，同时也涵盖针对不同行业和场景的实践案例，希望可以全方位地帮助你获取更多知识和技能。
windowsmicrosoft 企业社区
社区管理员
  • 王瑞MVP
  • 郑子铭
加入社区
  • 近7日
  • 近30日
  • 至今

加载中

查看更多榜单
社区公告

微软技术社区为中国的开发者们提供一个技术干货传播平台，传递微软全球的技术和产品最新动态，分享各大技术方向的学习资源，同时也涵盖针对不同行业和场景的实践案例，希望可以全方位地帮助你获取更多知识和技能。

予力众生，成就不凡！微软致力于用技术改变世界，助力企业实现数字化转型。

试试用AI创作助手写篇文章吧

+ 用AI写文章