C语言 深度优先搜索和广度优先搜索

微软技术分享 微软全球最有价值专家
优质创作者: 编程框架技术领域
领域专家: 操作系统技术领域
2024-01-30 09:12:14

前言

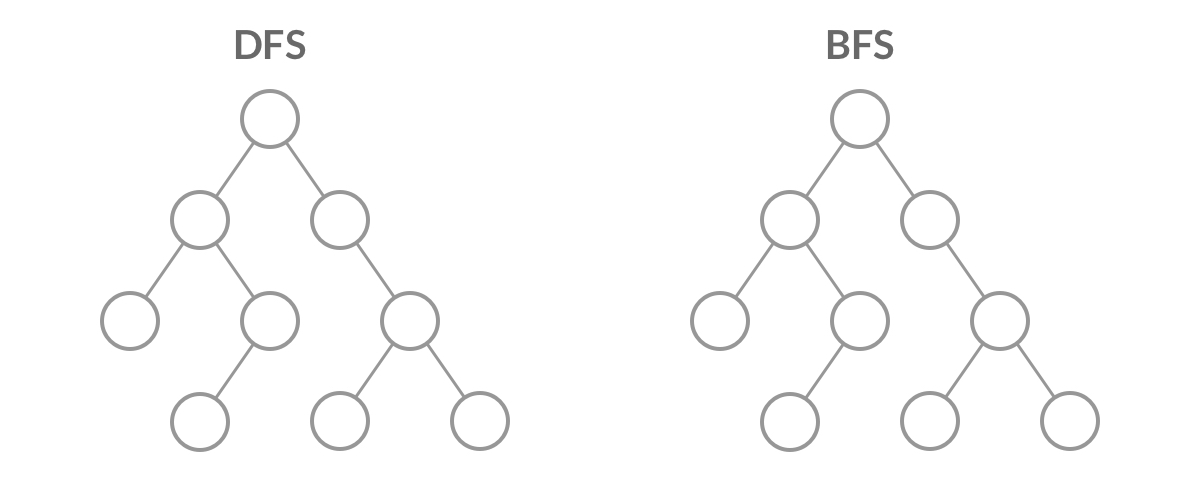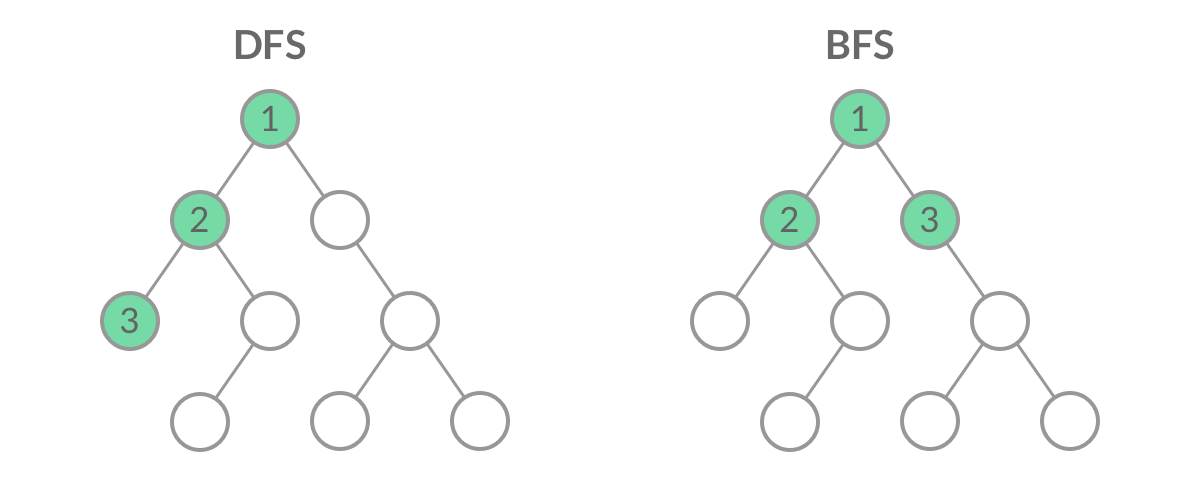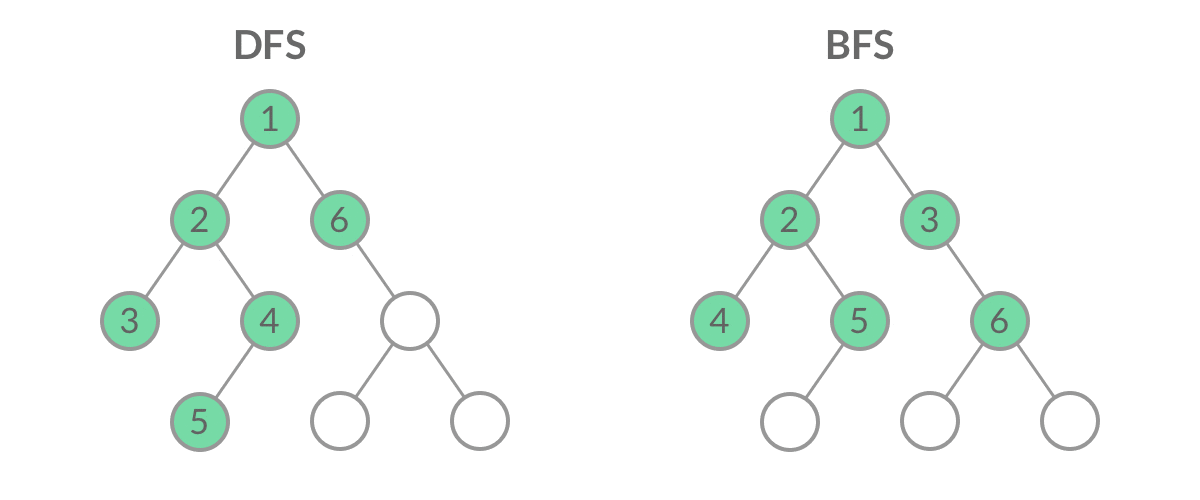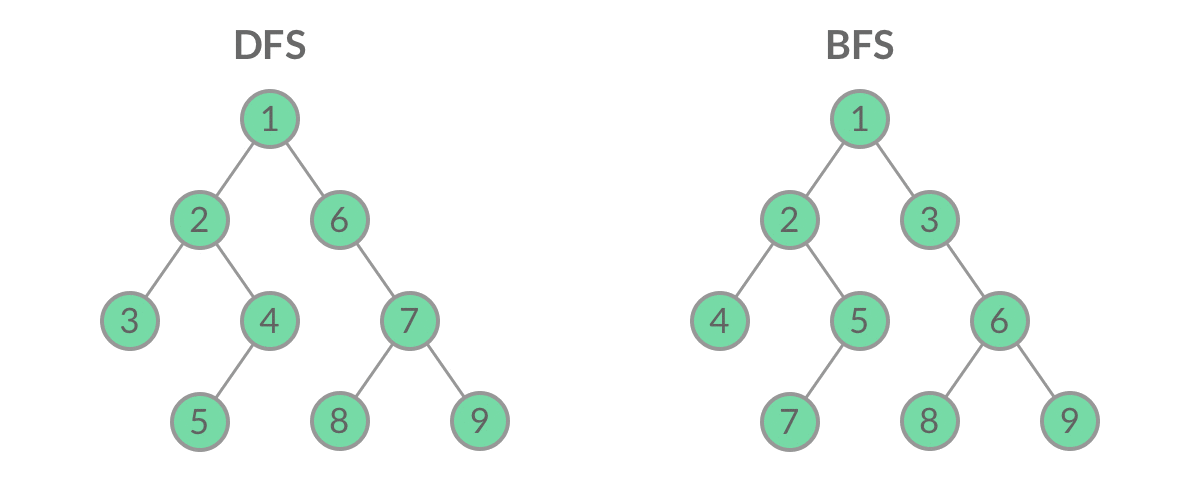
https://img-blog.csdnimg.cn/1b89a9f58e9c49aaa4aad62090ed6e1f.gif

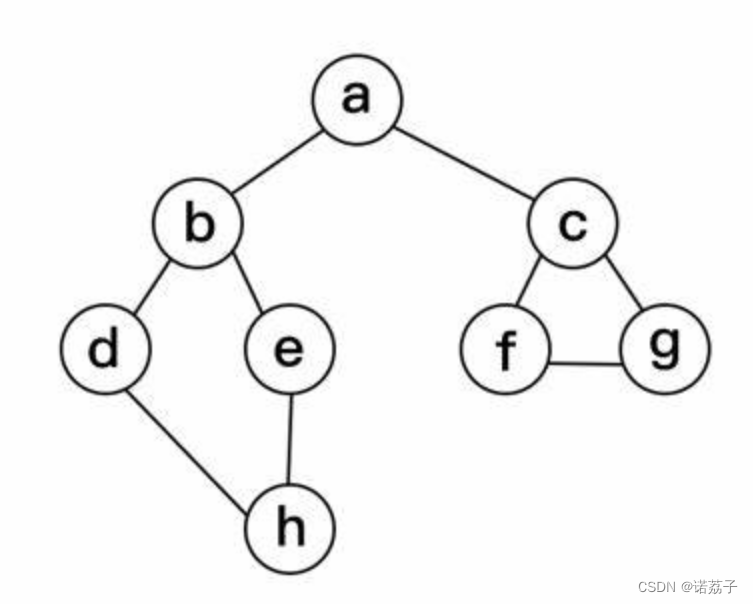
深度优先搜索（DFS）和广度优先搜索（BFS）是常用的图搜索算法。它们可以用于许多不同的应用，例如：

  • 解决迷宫问题：DFS和BFS可以用于寻找从起点到终点的路径。
  • 网络搜索：搜索引擎使用这些算法来构建网页索引和搜索结果。
  • 社交网络分析：DFS和BFS可以用于发现社交网络中的连通分量、关键人物和社区结构。
  • 生成树和图的遍历：DFS和BFS可以用于生成树和图的遍历，以及查找最短路径和最小生成树等。
  • 人工智能：DFS和BFS可以用于训练神经网络、搜索游戏树和解决决策问题等。

总之，DFS和BFS是非常常见和有用的算法，它们可以应用于许多不同的领域，包括计算机科学、人工智能、生物学、社会网络等。

 不太懂的看视频  QWQ（来自@码农论坛）

深度与广度优先搜索

深度优先搜索

深度优先搜索一般通过递归实现，也可以通过模拟栈实现。

基本流程如下：

1.创建一个栈并将起始顶点压入栈中。

2.当栈不为空时，进行以下操作：

  • 弹出栈顶元素，并将其标记为已访问。
  • 将该顶点的未被访问过的邻接点压入栈中。

3.重复步骤 2 直到栈为空。

这是算法递归实现函数：

//递归深度优先遍历
void DFS(ALGraph* G, int v, int* visited) {
    printf("%c ", G->vertices[v].data);//输出顶点v
    visited[v] = 1;//标记顶点v，表示已遍历
    ArcNode* p = G->vertices[v].first;//p指向v第一条依附顶点v的边
    while (p != NULL) {
        //递归遍历顶点v未访问的邻接点
        if (!visited[p->adjvex]) {
            DFS(G, p->adjvex, visited);
        }
        p = p->next;
    }
}

广度优先搜索

广度优先搜索使用队列来实现。

基本流程如下：

1.创建一个队列，并将起始顶点入队。 2.当队列不为空时，进行以下操作：

  • 出队一个顶点，输出该顶点。
  • 将该顶点的所有未被访问过的邻接点入队，并把它标记为已访问。

重复步骤 2 直到队列为空。

//广度优先遍历
void BFS(ALGraph* G, int* visited) {
    int e;//用来储存出队的顶点的顶点数组中的下标
    ArcNode* p = NULL;
    Queue* Q = InitQueue();//初始化队列
    Push(Q, 0);//把第一个顶点入队
    visited[0] = 1;//标记第一个顶点
    //循环结束条件为空队
    while (Pop(Q, &e)) {
        printf("%c ", G->vertices[e].data);//输出出队顶点
        p = G->vertices[e].first;//指针p指向依附顶点e的第一条边
        //将顶点e未访问的邻接点入队并标记
        while (p != NULL) {
            if (!visited[p->adjvex]) {
                Push(Q, p->adjvex);
                visited[p->adjvex] = 1;
            }
            p = p->next;
        }
    }
}

运行代码建立如下图所示的无向图并用深度优先搜索和广度优先搜索遍历：

https://img-blog.csdnimg.cn/5634f32e27bd4c129075d512d702a504.png

运行结果如下：

https://img-blog.csdnimg.cn/f7bb62ffb8a04661af5306511172b890.png

源代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <malloc.h>
#include<stdbool.h>
#define MVNum 100  //最大顶点数
typedef struct ArcNode {  //边表结点
    int adjvex;//邻接点在顶点数组中的下标
    struct ArcNode* next;//指向下一条边的指针
}ArcNode;

typedef struct VNode {   //顶点信息结构体
    char data;
    ArcNode* first;//指向第一条依附于该顶点的边的指针
}VNode, AdjList[MVNum];

typedef struct {   //图结构体
    AdjList vertices;//邻接表
    int vexnum, arcnum;//顶点数和边数
}ALGraph;

//查找
int LocateVex(ALGraph* G, char v) {
    int i;
    for (i = 0; i < G->vexnum; i++) {
        if (G->vertices[i].data == v) {
            return i;
        }
    }
    return -1;
}

//无向图邻接表的创建
ALGraph* CreateALGraph() {
    int i, j, k;
    char v1, v2;
    ALGraph* G = malloc(sizeof(ALGraph));
    printf("输入顶点数和边数:\n");
    scanf("%d%d", &G->vexnum, &G->arcnum);
    getchar();//吸收换行符
    printf("依次输入顶点信息：\n");
    for (i = 0; i < G->vexnum; i++) {
        scanf("%c", &G->vertices[i].data);
        G->vertices[i].first = NULL;
    }
    getchar();//吸收换行符
    //构造边表
    for (k = 0; k < G->arcnum; k++) {
        printf("输入一条边依附的两个顶点:\n");
        scanf("%c%c", &v1, &v2);
        getchar();//吸收换行符
        i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在邻接表数组中的下标
        ArcNode* p1 = malloc(sizeof(ArcNode));//生成新的边结点*p1
        p1->adjvex = i;//邻接点序号为i
        p1->next = G->vertices[j].first;//头插法插到顶点vj的边表头部
        G->vertices[j].first = p1;
        //因为是无向图，所以生成对称的边结点*p2
        ArcNode* p2 = malloc(sizeof(ArcNode));
        p2->adjvex = j;
        p2->next = G->vertices[i].first;
        G->vertices[i].first = p2;
    }
    return G;
}

//输出邻接表
void print(ALGraph* G) {
    int i;
    for (i = 0; i < G->vexnum; i++) {
        printf("顶点%c的邻结点有：", G->vertices[i].data);
        ArcNode* p = G->vertices[i].first;
        while (p != NULL) {
            printf(" %c", G->vertices[p->adjvex].data);
            p = p->next;
        }
        printf("\n");
    }
}

//递归深度优先遍历
void DFS(ALGraph* G, int v, int* visited) {
    printf("%c ", G->vertices[v].data);//输出顶点v
    visited[v] = 1;//标记顶点v，表示已遍历
    ArcNode* p = G->vertices[v].first;//p指向v第一条依附顶点v的边
    while (p != NULL) {
        //递归遍历顶点v未访问的邻接点
        if (!visited[p->adjvex]) {
            DFS(G, p->adjvex, visited);
        }
        p = p->next;
    }
}


typedef struct QNode {
    int data;
    struct QNode* next;
}QNode;
typedef struct {
    QNode* front;
    QNode* rear;
}Queue;
Queue* InitQueue() {
    Queue* Q = malloc(sizeof(Queue));
    QNode* t = malloc(sizeof(QNode));
    t->next = NULL;
    Q->front = t;
    Q->rear = t;
    return Q;
}
void Push(Queue* Q, int e) {
    QNode* t = malloc(sizeof(QNode));
    t->data = e;
    t->next = NULL;
    Q->rear->next = t;
    Q->rear = t;
}
bool Pop(Queue* Q, int* e) {
    if (Q->front == Q->rear)    return false;
    QNode* p = Q->front->next;
    *e = p->data;
    if (Q->rear == p) {
        Q->rear = Q->front;
    }
    Q->front->next = p->next;
    free(p);
    return true;
}

//广度优先遍历
void BFS(ALGraph* G, int* visited) {
    int e;//用来储存出队的顶点的顶点数组中的下标
    ArcNode* p = NULL;
    Queue* Q = InitQueue();//初始化队列
    Push(Q, 0);//把第一个顶点入队
    visited[0] = 1;//标记第一个顶点
    //循环结束条件为空队
    while (Pop(Q, &e)) {
        printf("%c ", G->vertices[e].data);//输出出队顶点
        p = G->vertices[e].first;//指针p指向依附顶点e的第一条边
        //将顶点e未访问的邻接点入队并标记
        while (p != NULL) {
            if (!visited[p->adjvex]) {
                Push(Q, p->adjvex);
                visited[p->adjvex] = 1;
            }
            p = p->next;
        }
    }
}

int main() {
    ALGraph* G = CreateALGraph();
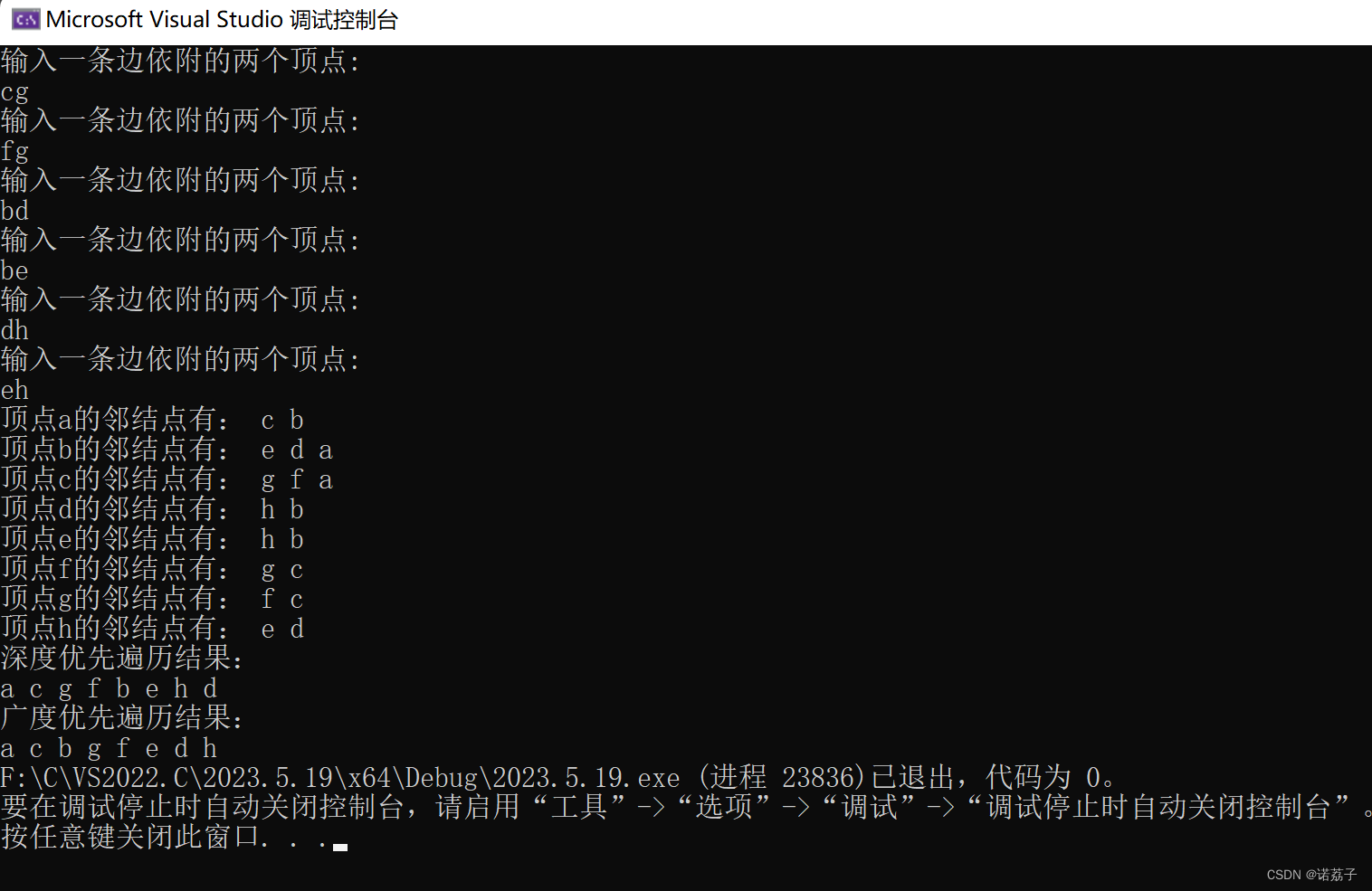
    print(G);
    int visited_1[MVNum] = { 0 };
    printf("深度优先遍历结果：\n");
    DFS(G, 0, visited_1);
    int visited_2[MVNum] = { 0 };
    printf("\n广度优先遍历结果：\n");
    BFS(G, visited_2);
}

总结

  • 深度优先搜索是从一个节点开始，沿着一条路径一直走到底，如果走到了死路，就回退到上一个节点，再继续走其他路径，直到遍历完整个图。
  • 广度优先搜索是从一个节点开始，先访问这个节点的所有邻居节点，然后依次访问这些邻居节点的邻居节点，直到遍历完整个图。

两者的主要区别在于搜索的顺序不同，深度优先搜索的搜索顺序是一条路走到黑，直到遇到死路才回退，而广度优先搜索的搜索顺序是逐层遍历，先遍历距离起始节点为1的节点，再遍历距离起始节点为2的节点，以此类推。

文章来源： https://blog.csdn.net/m0_73070900/article/details/130868251
版权声明： 本文为博主原创文章，遵循CC 4.0 BY-SA 知识共享协议，转载请附上原文出处链接和本声明。

...全文
58 回复 打赏 收藏 转发到动态 举报
写回复
用AI写文章
回复
切换为时间正序
请发表友善的回复…
发表回复
C语言实现：八数码问题的深度优先搜索、广度优先搜索、过程表示（全）
人工智能实验： 实现结果：给定八数码的起始状态和目标状态，程序可以自动计算出所需要的步数，并能打印出每一步的变化。 本资源包括：使用C语言实现 ①使用深度优先搜索来解决八数码问题 ②使用广度优先搜索来解决八数码问题 ③使用过程式表示和实现八数码问题 以及相关代码详细注释 过程式知识表示是将有关某一问题领域的知识， 连同如何使用这些知识的方法，均隐式的表达为 一个求解问题的过程，每个过程是一段程序，完成对具体情况的处理。过程式不像陈述式那样具有固定的形式，如何描述知识完全取决于具体问题。 深度搜索：以栈为容器。由于每次将可能的新状态入栈，并标记为已经搜索到，当一直深入时便会遇到下一步可能搜索到的所有状态都已经标记为搜索过了，即没有可入栈的，这条深度搜索路线结束，下次出栈为栈顶状态，即另一条深度搜索路线。因为进行搜索之前判断了是否可达，所以进入搜索必有解，那么会按上述进行，直到找到目标状态。 最简单的方法是在上述深度搜索代码上进行改动，即可进行广度搜索。 深度是将集合中的元素从末尾取出，即和栈的特点相同，那么将先进后出变为先进先出，即将栈改成了队列。
深度优先、广度优先搜索算法C语言版
数据结构课程中的深度优先搜索算法、广度优先搜索算法的C语言程序，在Turbo C 2.0上调试通过。
图的深度、广度优先遍历（c语言）
本程序方便的实现了图的深度、广度优先遍历。是数据结构中的一部分，现与大家分享
深度优先及广度优先算法c语言源码
深度优先及广度优先算法c语言源码，深度优先及广度优先算法c语言源码
图的广度优先，深度优先算法 c语言描述
图的广度优先，深度优先算法 c语言描述版。
微软技术社区

6,135

社区成员

37,287

社区内容

发帖
与我相关
我的任务
社区描述
微软技术社区为中国的开发者们提供一个技术干货传播平台，传递微软全球的技术和产品最新动态，分享各大技术方向的学习资源，同时也涵盖针对不同行业和场景的实践案例，希望可以全方位地帮助你获取更多知识和技能。
windowsmicrosoft 企业社区
社区管理员
  • 王瑞MVP
  • 郑子铭
加入社区
  • 近7日
  • 近30日
  • 至今

加载中

查看更多榜单
社区公告

微软技术社区为中国的开发者们提供一个技术干货传播平台，传递微软全球的技术和产品最新动态，分享各大技术方向的学习资源，同时也涵盖针对不同行业和场景的实践案例，希望可以全方位地帮助你获取更多知识和技能。

予力众生，成就不凡！微软致力于用技术改变世界，助力企业实现数字化转型。

试试用AI创作助手写篇文章吧

+ 用AI写文章