图的基本概念

图

图 (graph) 是一个二元组 其中V(G)是非空集，称为 点集 (vertex set)，对于V中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)，简称 点；E(G)为V(G)各结点之间边的集合，称为 边集 (edge set)。

常用  表示图。

当 V,E都是有限集合时，称 G 为 有限图。

当 V 或  E是无限集合时，称 G 为 无限图。

图有多种，包括 无向图 (undirected graph)，有向图 (directed graph)，混合图 (mixed graph) 等。

若 G为无向图，则 E 中的每个元素为一个无序二元组 ，称作 无向边 (undirected edge)，简称 边 (edge)，其中 。设 ，则 u 和 v 称为 e的 端点 (endpoint)。

若 G为有向图，则 E中的每一个元素为一个有序二元组 ，有时也写作 ，称作 有向边 (directed edge) 或 弧 (arc)，在不引起混淆的情况下也可以称作 边 (edge)。设 ，则此时 u 称为 e 的 起点 (tail)， 称v为 e 的 终点 (head)，起点和终点也称为 e 的 端点 (endpoint)。并称 u是 v 的直接前驱，v 是 u 的直接后继。

若 G为混合图，则 E 中既有 有向边，又有 无向边。

若 G的每条边  都被赋予一个数作为该边的 权，则称 G为 赋权图。如果这些权都是正实数，就称 G为 正权图。

图 G的点数  也被称作图G的 阶 (order)。

形象地说，图是由若干点以及连接点与点的边构成的。

树和最小生成树

树

一、定义 

无圈的连通图

二、性质

1、任何树图中必存在次为1的点

2、具有n个顶点的树图的边数恰好为（n-1)条

3、任何具有n个点、n-1条边的连通图是树图

生成树

一、概念

如果图G的生成子图是一棵树，则该树T称为图G的生成树

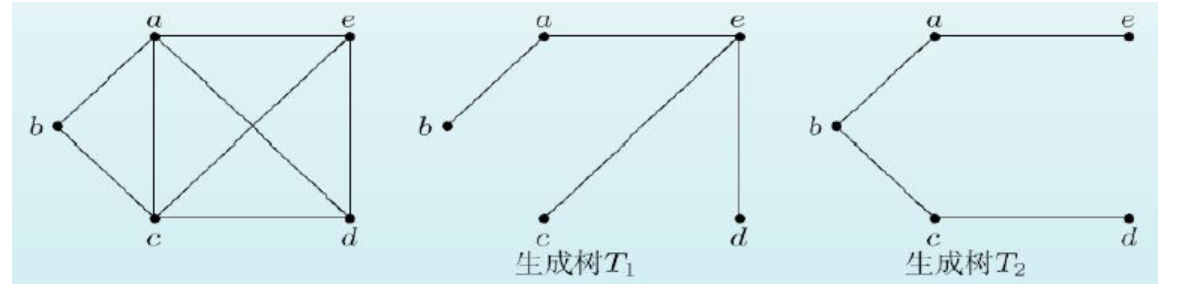
二、定理

图G有生成树的充分必要条件为图是连通图

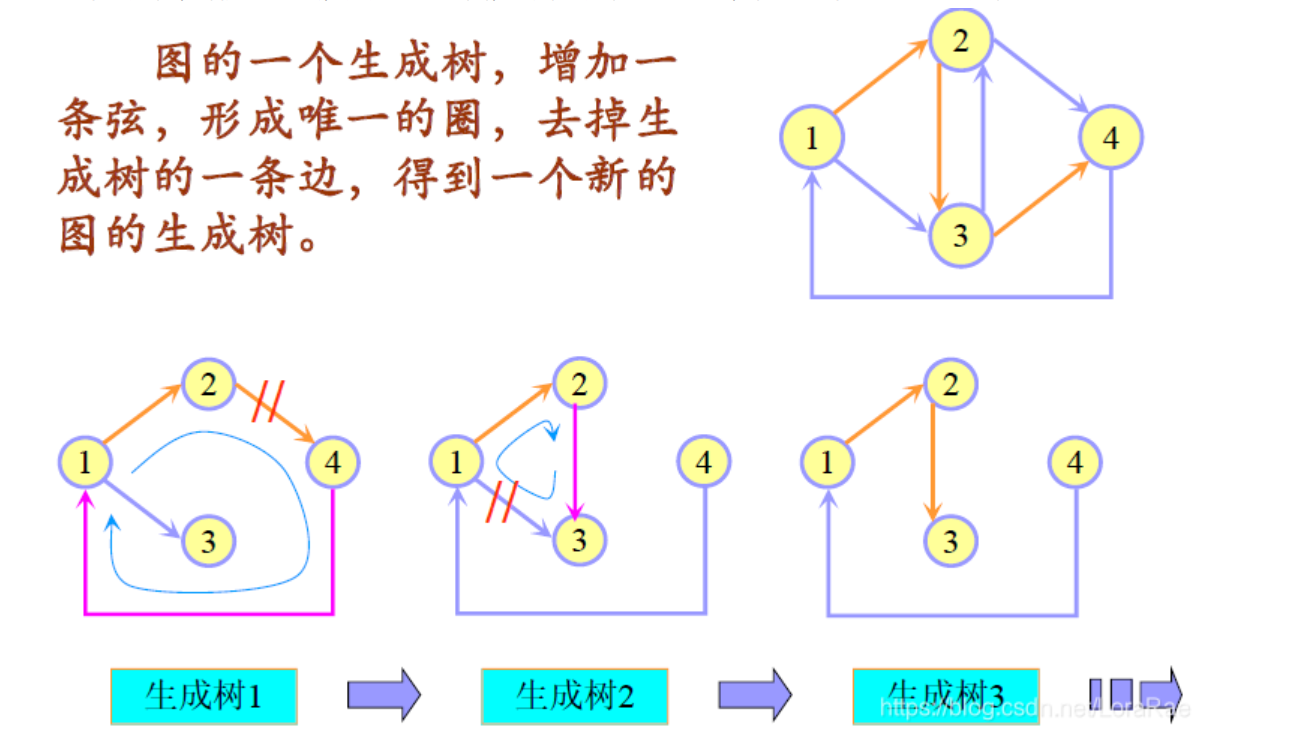
三、求法

1、破圈法

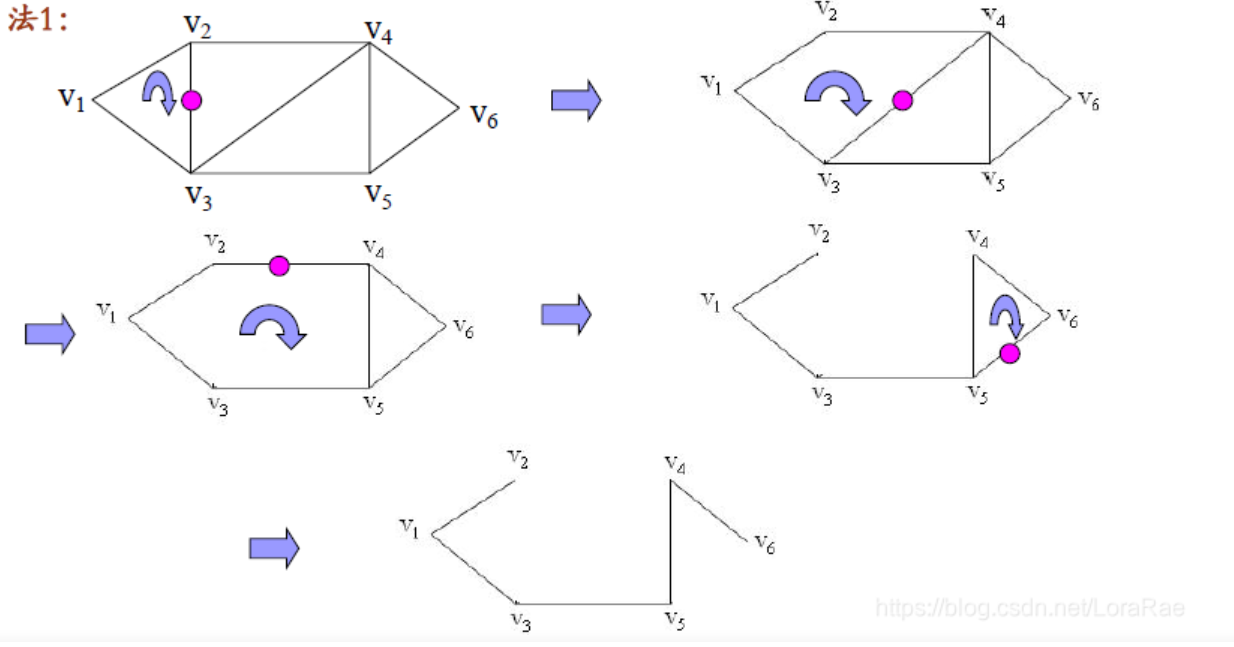
2、避圈法

最小生成树

一、概念

树的权最小的生成树T*称为最小生成树

二、求法

1、破圈法

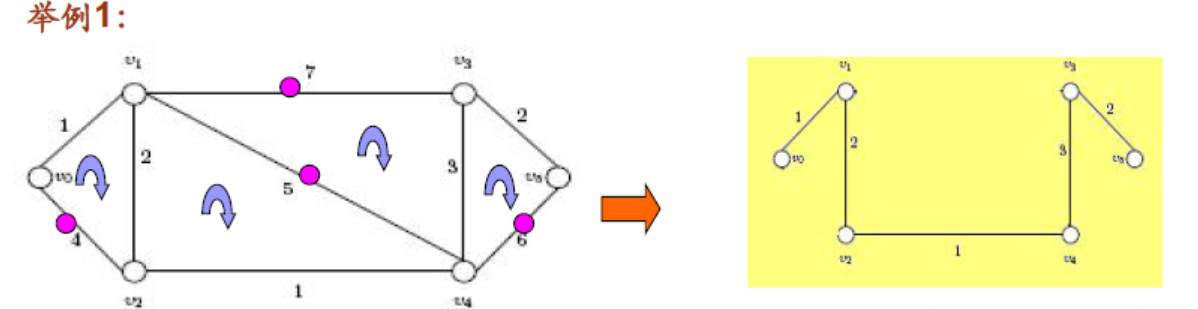
2、避圈法

最短路问题

一、定义

任意两点之间距离最短

二、权

距离的代称，也可以为时间费用

三、举例

设备更新、管道铺设 、线路安排、厂区布局

四、类型

1、求图中某一顶点到其它顶点的最短路径
2、 求图中每一对顶点之间的最短路径

五、求法

1、权W(e) ≥0时   使用Dijkstra算法（标号法）

2、权W(e) ＜0时  使用逐次逼近算法。