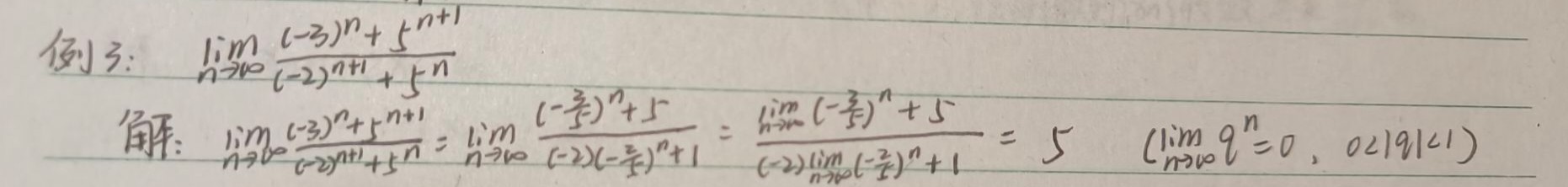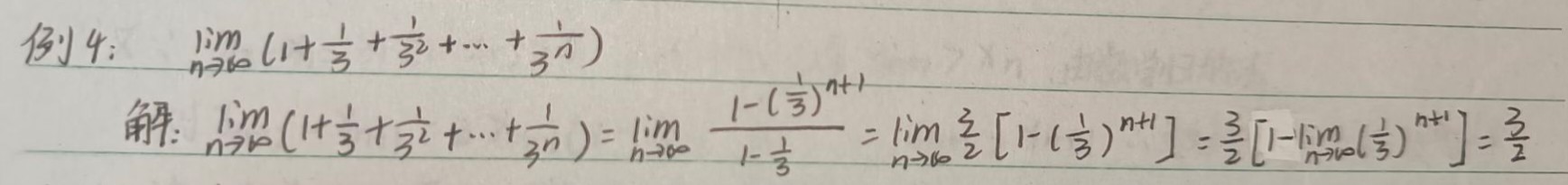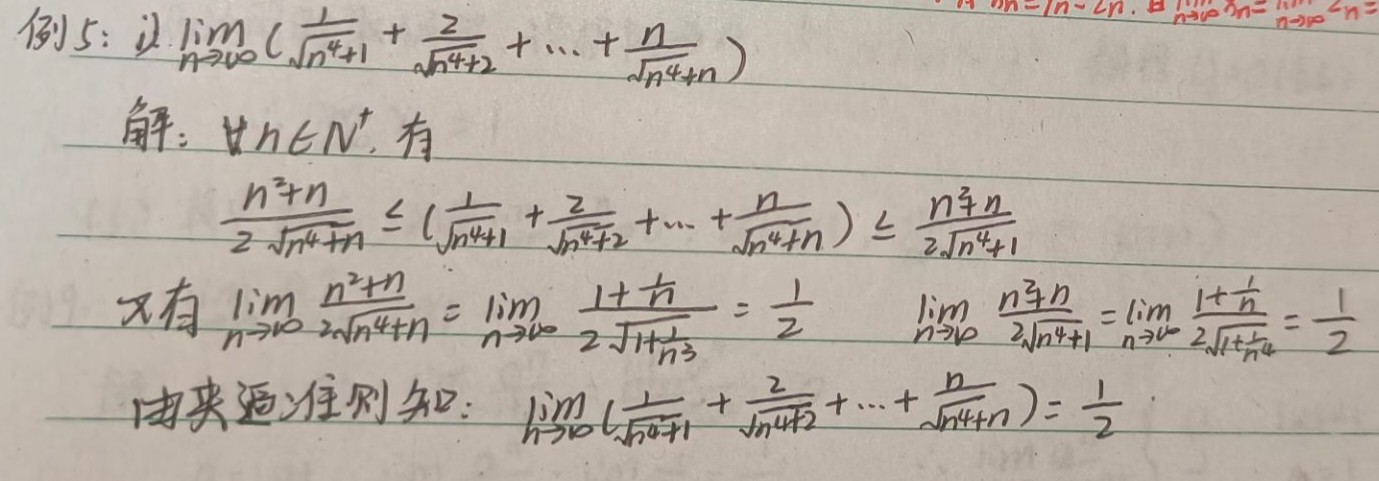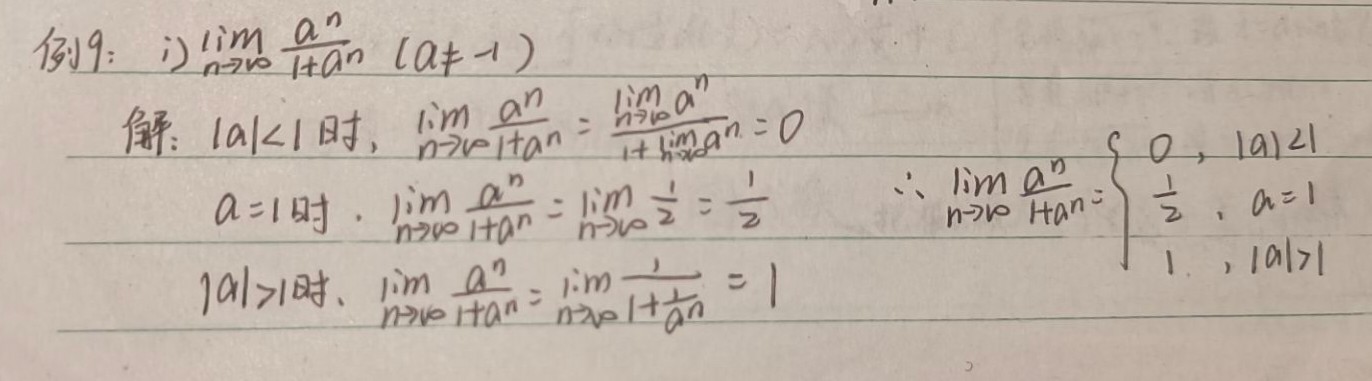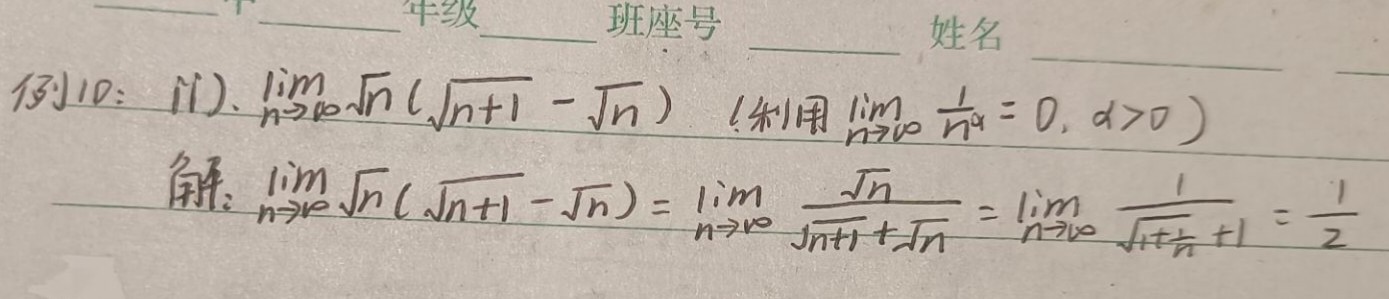简要介绍:
数学分析又称高级微积分,分析学中最古老、最基本的分支。一般指以微积分学和无穷级数一般理论为主要内容,并包括它们的理论基础(实数、函数和极限的基本理论)的一个较为完整的数学学科。而数列的极限问题是我们学习的一个比较重要的部分,同时,极限的理论也是高等数学的基础之一。数列极限的问题作为微积分的基础概念,其建立与产生对微积分的理论有着重要的意义。
接下来是我的笔记关于求数列极限的方法:
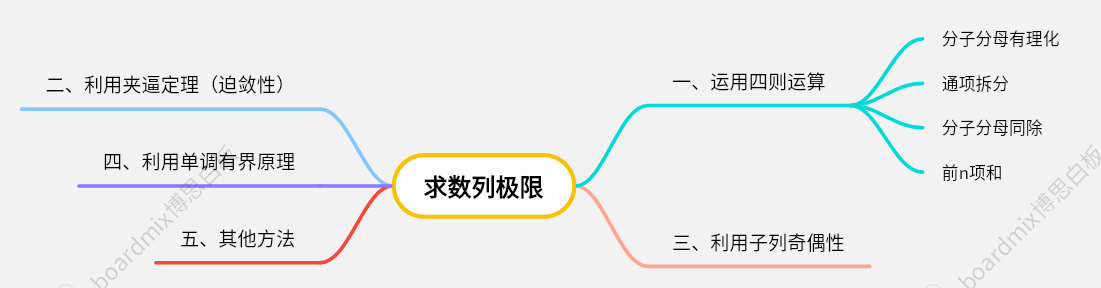
一、运用四则运算
①分子分母有理化(是在二次根式中分母原为无理数,而将该分母化为有理数的过程)
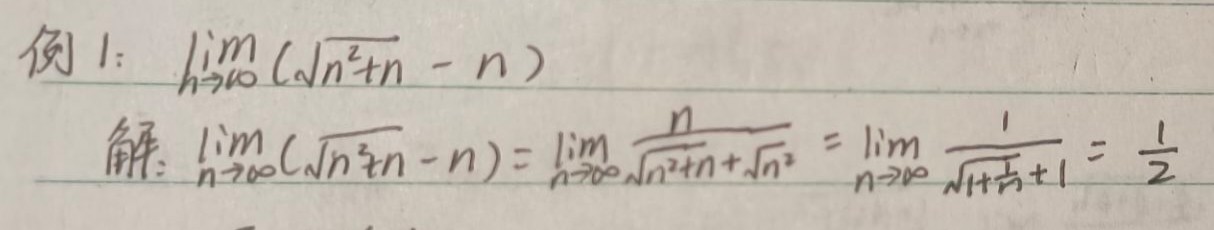
②通项拆分
(是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的。)
 ③分子分母同除
③分子分母同除
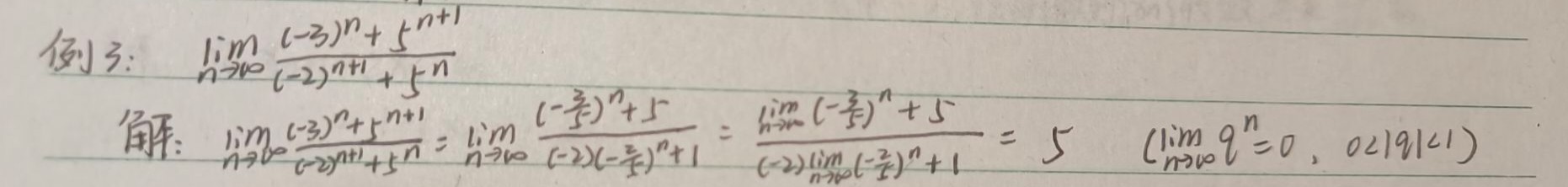
④前n项和
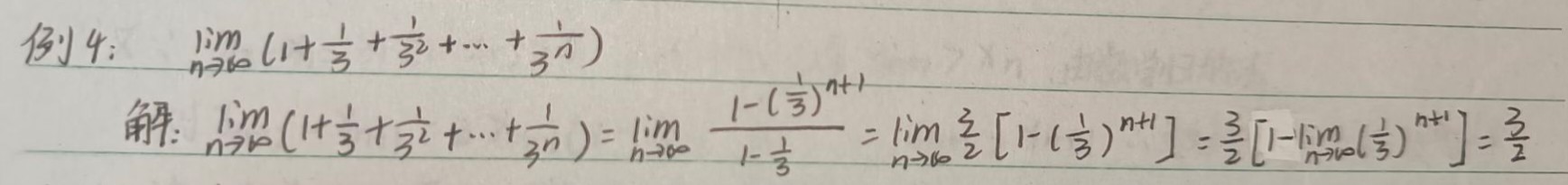
二、利用夹逼定理(迫敛性)
(设函数g(x)≤f(x)≤h(x),如果在自变量的同一变化过程中limg(x)=A,limh(x)=A,则必有limf(x)=A。)
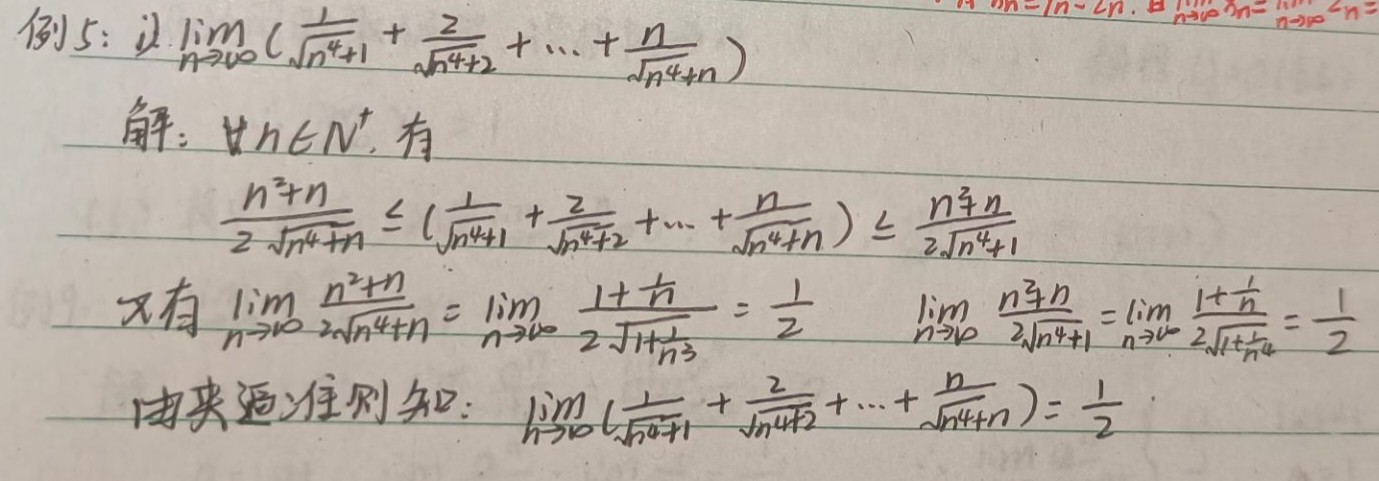

三、利用子列奇偶性
四、利用单调有界原理
(指的是单调有界数列必收敛(有极限)。这一原理只能用于证明数列极限的存在性)

五、其他方法
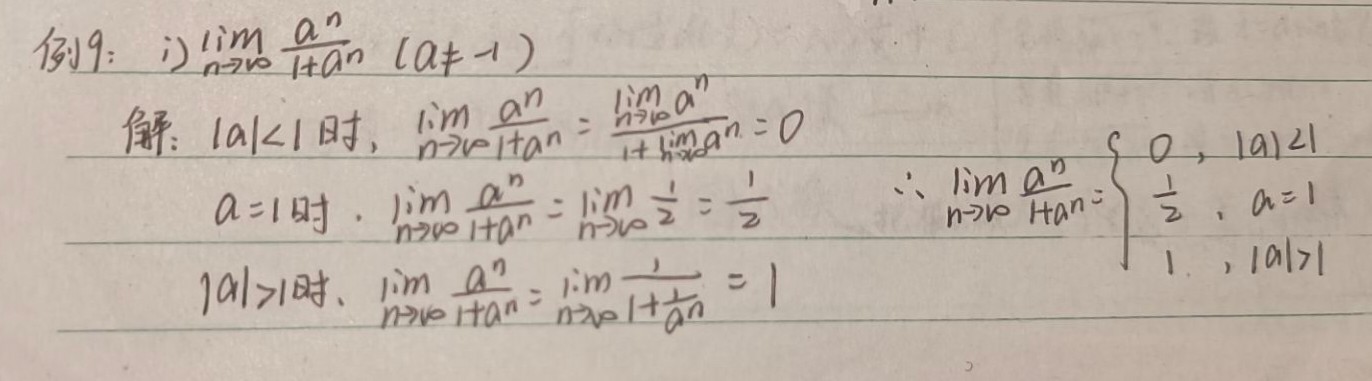
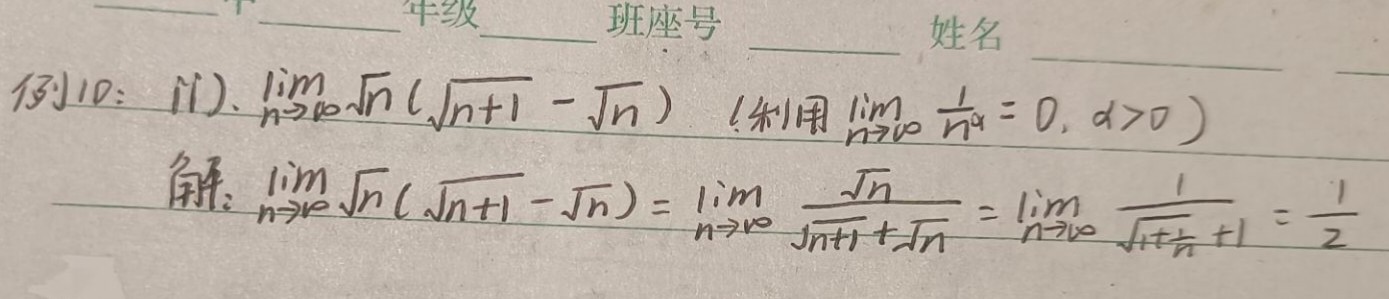
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享
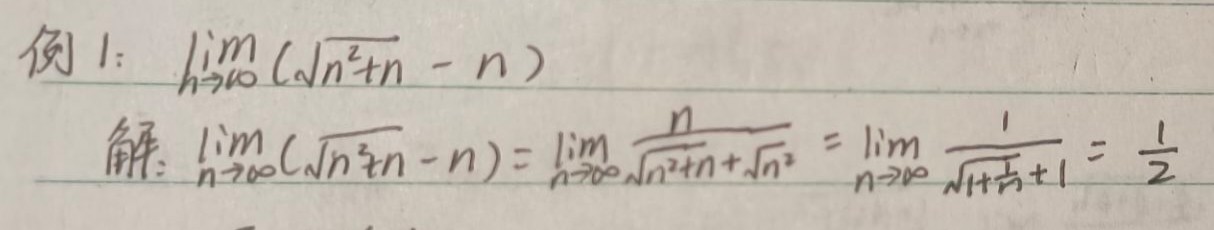
 ③分子分母同除
③分子分母同除