线性规划 及 单纯形法

线性规划及单纯形法
一、一般线性规划问题的数学模型
①一般线性规划问题的数学模型可表示为一下几种形式：
s.t.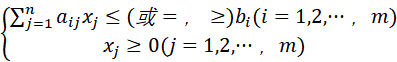

用向量形式表达时，上述模型可写为：

max(或min)z=CX

s.t.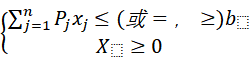
式中C=（c1，c2，…，cn），X=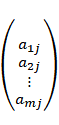，=，b=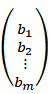

用矩阵形式表达时，上述模型可写为：
max(或min)z=CX

s.t.

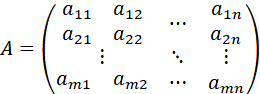
A称为约束方程组变量的系数矩阵，简称约束变量的系数矩阵。

②线性规划问题的解
可行解：满足约束条件的解，全部可行解的集合称为可行域。
最优解：使目标函数达到最大值的可行解称为最优解。


二、图解法（只能用来求解只具有两个变量的线性规划问题）

解的情况有：唯一最优解，无穷多最优解，无界解，无可行解

（1）若线性规划问题的可行解存在，则可行域是一个凸集；
（2）若线性规划问题的最优解存在，则最优解或最优解之一（如果有无穷多的话)一定能够在可行域(凸集）的某个项点找到；

（3）解题思路是，先找出凸集的任一顶点，计算在顶点处的目标函数值；比较周围相邻顶点的目标函数值是否比这个值更优，如果为否，则该顶点就是最优解的点或最优解的点之一，否则转到比这个点的目标函数值更优的另一顶点；重复上述过程，一直到找出使目标函数值达到最优的顶点为止。


三、单纯形法计算步骤

第一步：求出线性规划的初始基可行解，列出初始单纯形表

第二步：进行最优性检验

第三步：从一个基可行解转换到另一个目标函数值更大的基可行解，列出新的单纯形表

第四步：重复第二、三步一直到计算终止