关于不定积分的计算方法

在微分学中，不定积分是定积分、二重积分等的基础，学好不定积分十分重要。然而在学习过程中发现不定积分不像微分那样直观和“有章可循”。故本文是对不定积分解题方法的归纳和总结。

不定积分看似形式多样，变幻莫测，但并不是毫无解题规律可言。本文所总结的是一般规律，并非所有相似题型都适用，具体情况仍需要具体分析。

首先是本文章的思维导图，再从具体的例题说明不同的类型如何进行解题。

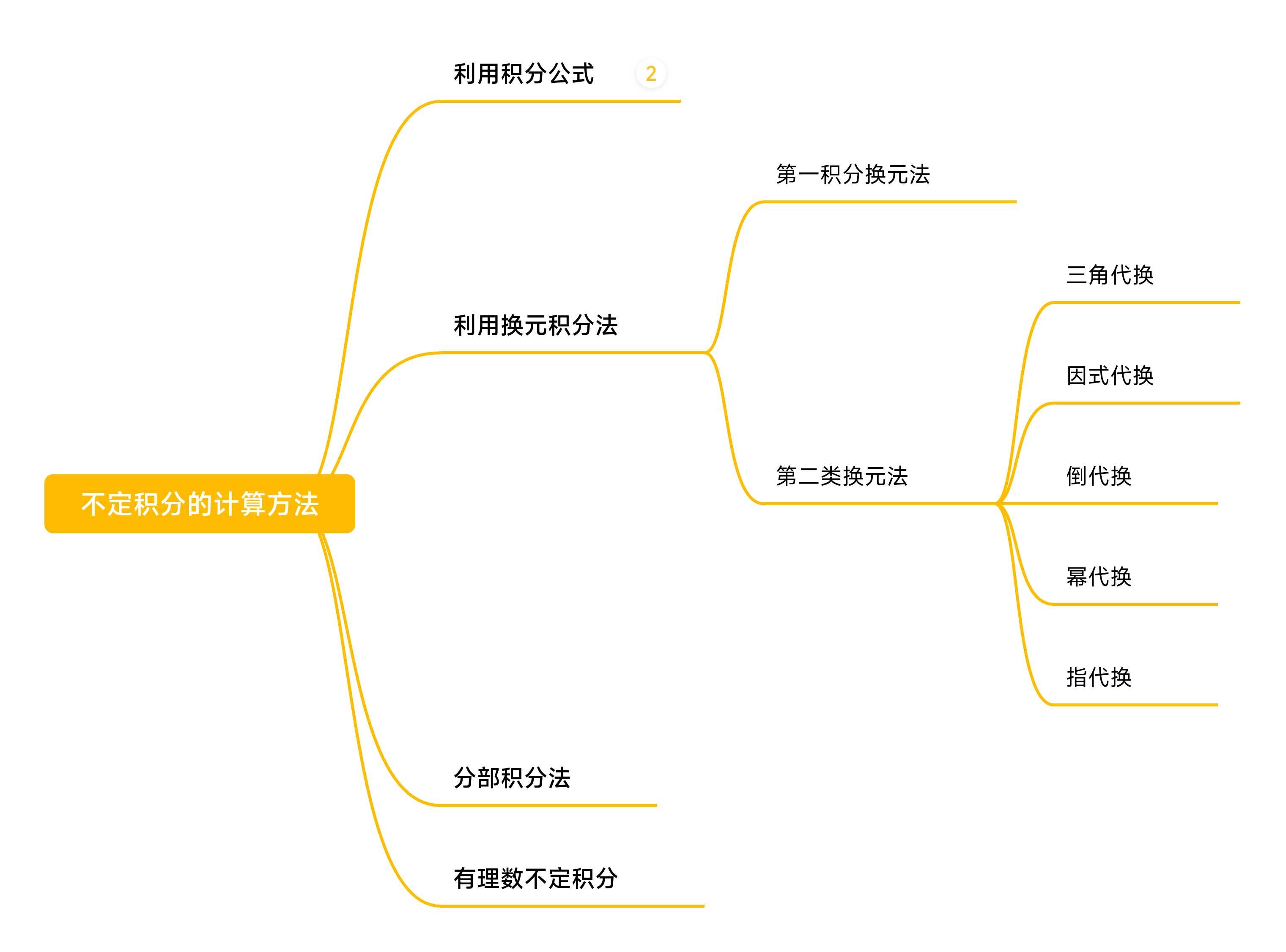
一、利用积分公式（根据不定积分的性质和基本积分公式）

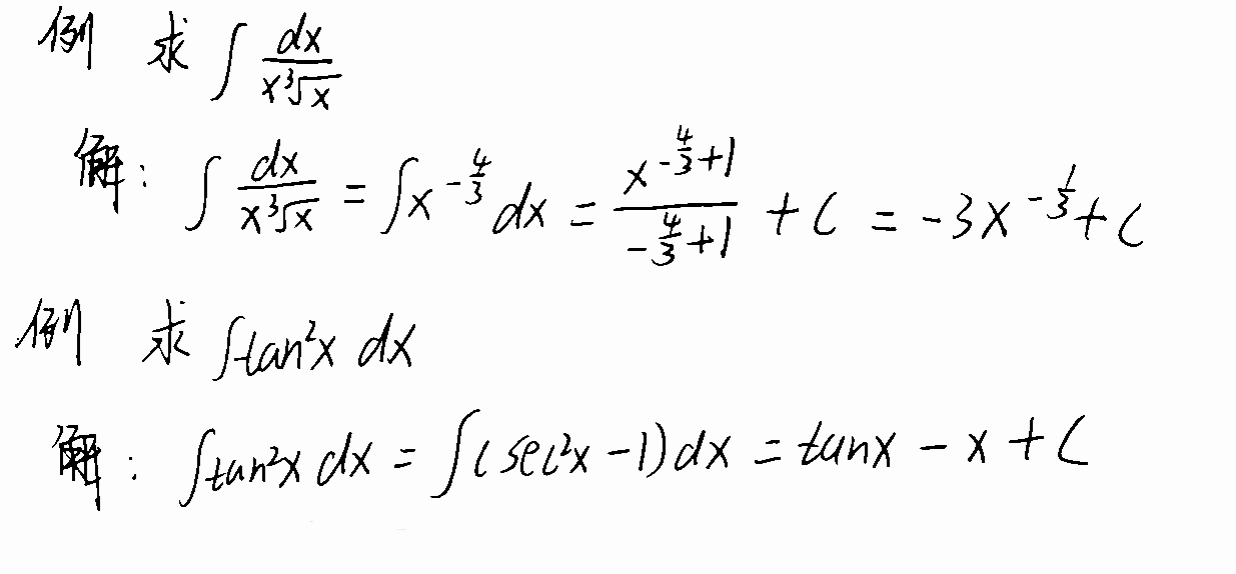
 二、利用换元积分法

（一）第一积分换元法（凑微分法）

用凑微分求解时，先要观察被积函数，需要放进导数项的内容，为积分做准备。

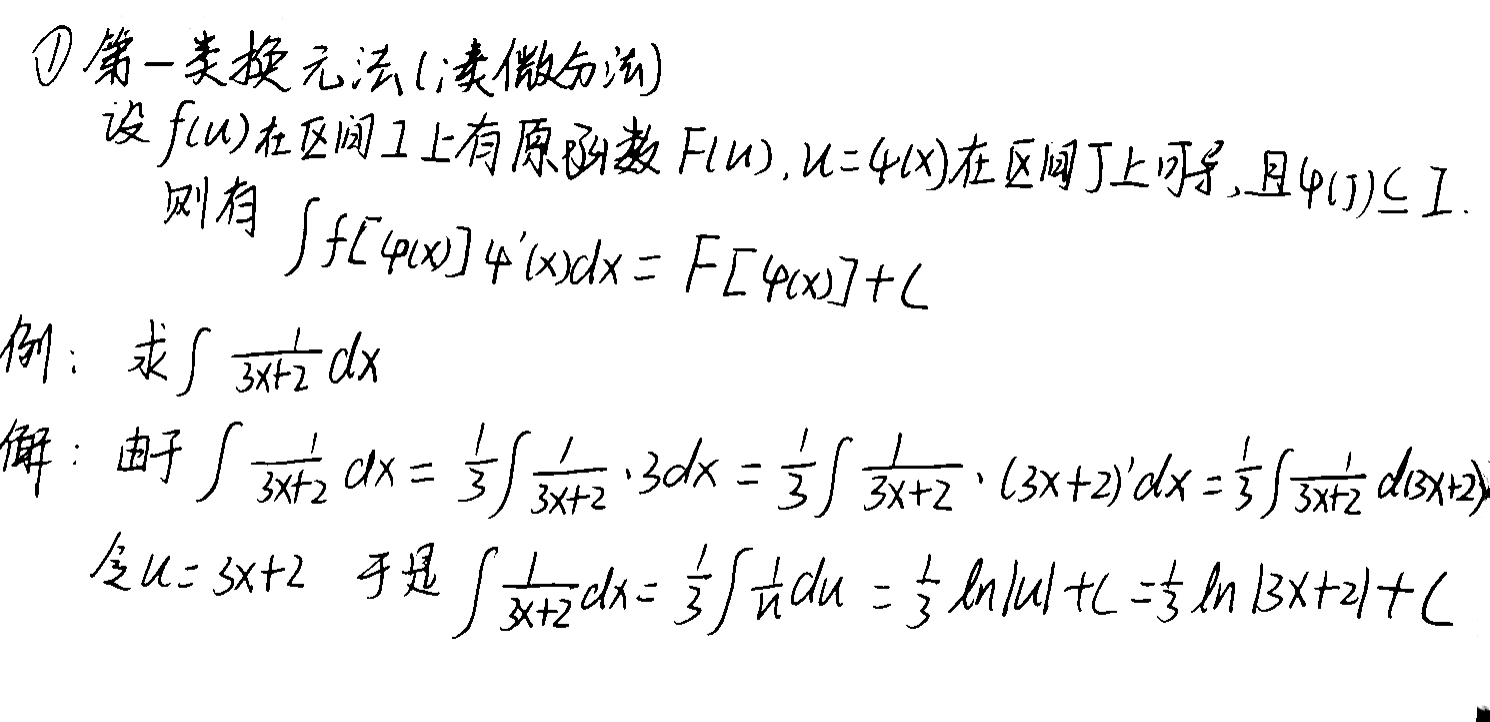
 （二）第二类换元法

第二类换元主要针对多形式的无理根式。熟记常见的几个。

1、三角代换（被积函数含有二次根式的情况）

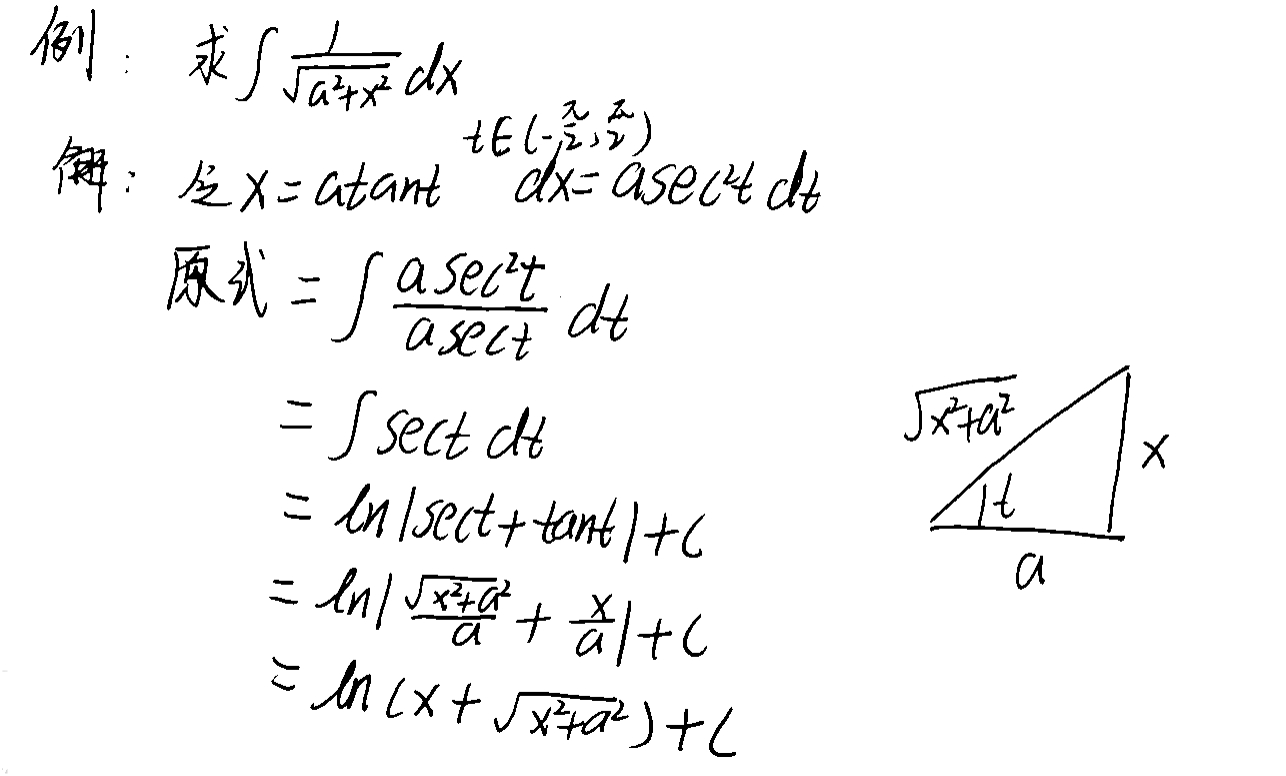
 2.因式代换

3.倒代换 

当被积函数是分母次数较高的有理函数或根式有理数式时，用x=1/t替代。 

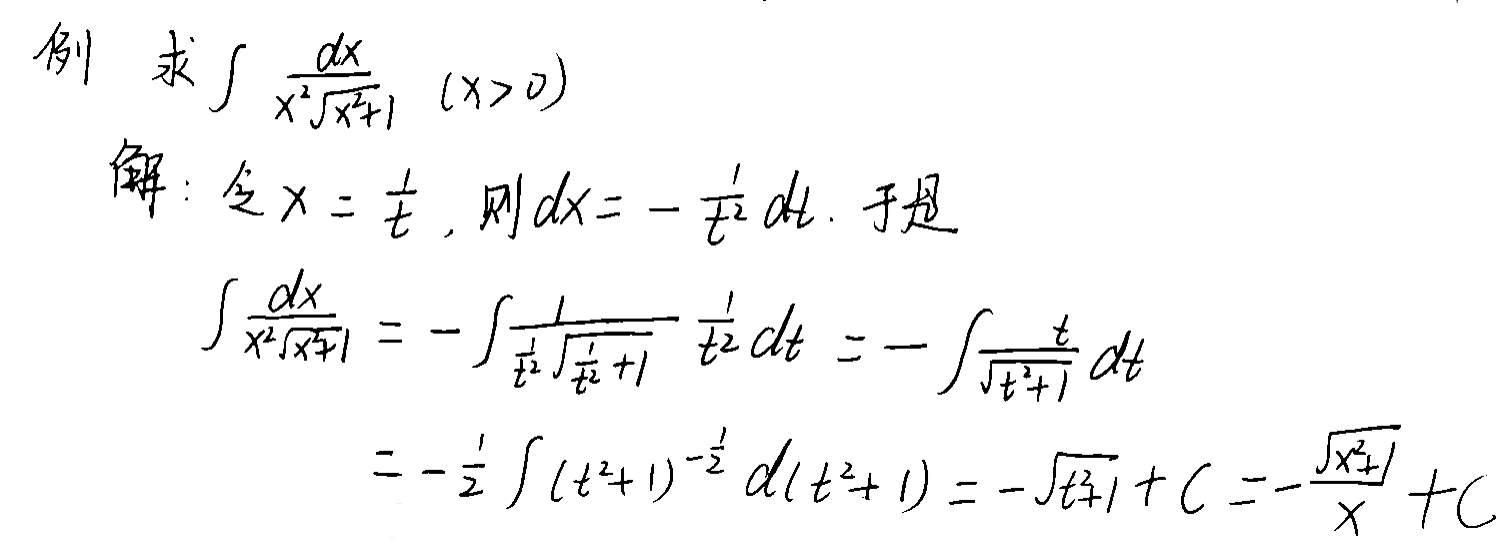
 4.幂代换

被积函数含有开n次方根时，用t整体代换。

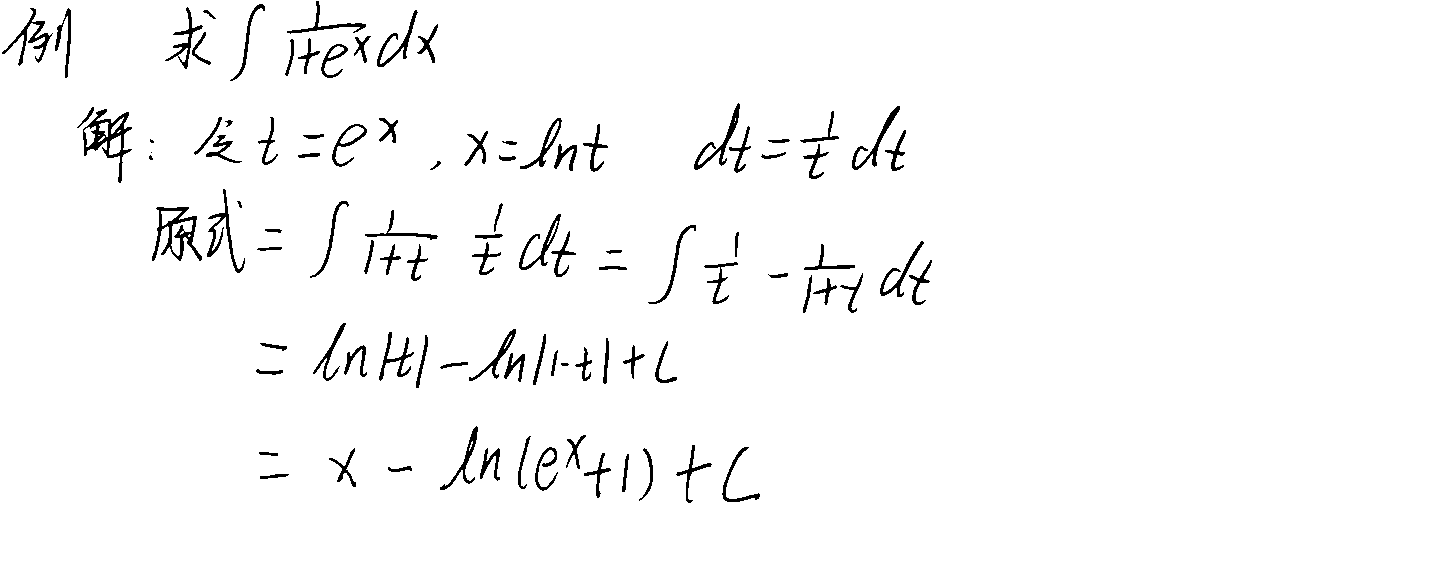
 三、分部积分法

分部积分法采用比较迂回的技巧，规避难点，先积简单部分，最终全部完成。

 四、有理函数不定积分

有理函数先化为多项式和真分式之和，再将真分式分解为若干个部分分式之和。有时过于复杂，可用递推公式。