4,402
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享本文介绍ISSCC34.6文章,题目是《A 28nm 72.12TFLOPS/W Hybrid-Domain Outer-Product Based Floating-Point SRAM Computing-in-Memory Macro with Logarithm Bit-Width Residual ADC》(一种28nm 72.12TFLOPS/W混合域外积浮点SRAM存内计算宏单元,具有对数位宽残差ADC)。该研究结合数字存内计算电路结构和模拟存内计算电路结构的特点,提出了一种新型数模混合存内计算架构,并立足于高精确计算,展开了一系列研究。下面是对文章基本信息及创新点的详细介绍。
一、基本信息介绍
本文第一作者为中国科学院微电子研究所的2021级直博生袁易扬,共同作者来自中国科学院大学、北京理工大学、澳门大学等研究单位。
本研究立足于当前存内计算技术面临的计算精度不足以满足新型AI应用需求的问题,分析当前数字和模拟两种存内计算范式所面临的挑战:(1)模拟存内计算技术虽然因为使用晶体管计算而具备较低的阵列输入消耗,但ADC和阵列输出消耗高;数字存内计算技术中的加法树器件虽然具备较低的阵列输出和移位累加消耗,但计算阵列由于使用逻辑门而具备较高的阵列输入消耗。如何结合两种计算范式的优势,以实现最佳能效是当前存内计算技术所面临的挑战。(2)ADC器件的精度、吞吐量和面积难以取得平衡,是模拟存内计算技术的重要挑战。(3)数字存内计算核内部需要多个多级加法树,以实现高比特精度部分积和内积的计算。并基于上述挑战提出了三个创新点。
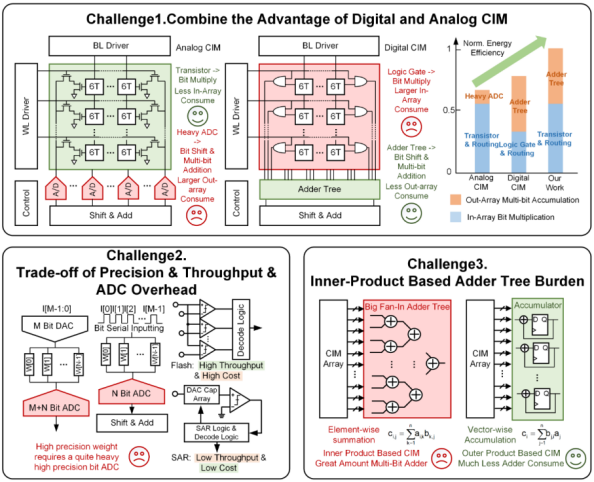
图1 文章背景及面临的挑战
二、创新点解析
本文提出了一种混合域8b CIM宏,分别使用模拟CIM进行高效阵列内比特乘法、使用数字CIM进行高效阵列外多比特移位累加,综合利用了模拟和数字CIM的优势。其中,模拟CIM比数字CIM的内嵌逻辑门可以用更少的晶体管进行更高效的阵列内比特乘法,而数字CIM加法器在进行阵列外多位移位和累加时比大型高精度模拟CIM ADC的效率要高得多。因此,本文提出一种方法来分离比特乘法和计算过程中的多比特移位和累加,以结合模拟和数字CIM的优势。
以具体的乘累加操作为例,如下图2所示,对于W[7:0]×A[7:0]的乘累加操作,首先通过如下所示的公式转换可以将其分为乘法和累加两种操作,分别用橙色和蓝色标注,橙色部分用模拟CIM执行,蓝色部分用数字CIM执行。
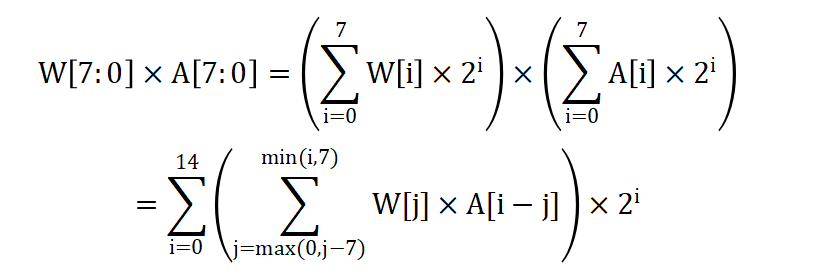
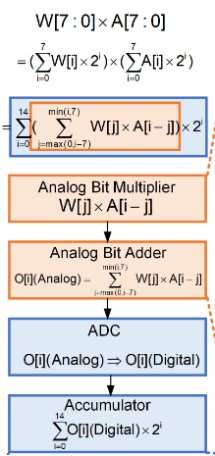
图2 数模混合公式转换
如下图3所示,在具体的电路实施上,模拟CIM用一个由传输端口和电流镜组成的阵列来处理乘法操作;数字CIM通过8周期累加对经过ADC转换之后的数据进行移位累加操纵。这种电路结构重复结合了模拟和数字CIM的优点,从而显著地提高了CIM宏性能。
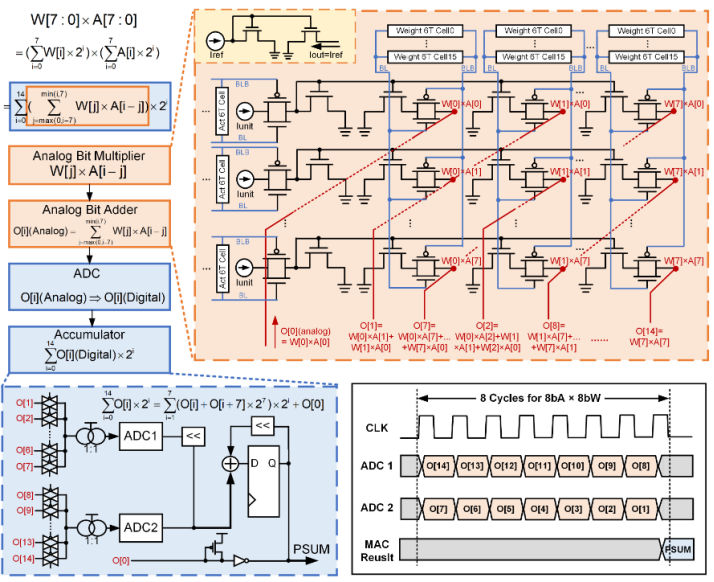
图3 数模混合电路示意图
本文的数模混合方式的原理为将乘累加操作分别拆分为乘法和累加操作,再根据模拟和数字CIM的优势,分别让其进行乘法和累加操作。同年ISSCC 34.3中也提出了一种新颖的数模混合结构——“类闪电式”,这种数模混合方式的原理为拆分乘累加的比特数,分别用数字和模拟CIM进行处理。图4展示了“类闪电式”混合SRAM CIM宏架构,支持累加器长度可扩展。图中蓝色为数字计算部分,黄色为模拟计算部分,通过将高位、低位数字单元(HDU与LDU)与高位、低位模拟单元(HAU、LAU)进行排列组合(两个子阵列与HDU和LDU对组合,四个子阵列与HDU和LAU对组合,其余两个子阵列与HAU和LAU对组合),以此来进行高效的8位整数乘累加操作。这种方案大大减少了所需的ADC转换次数和存储需求,同时支持更大的累加长度,而无需存储大量的部分和,适合于CNN与Transformer。
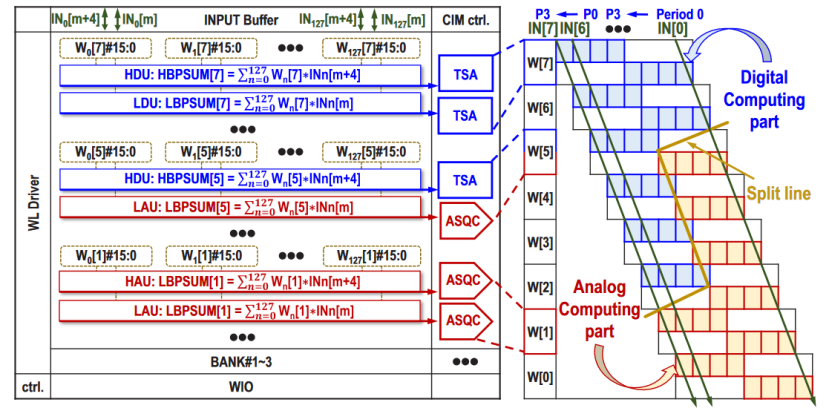
图4 闪电式混合SRAM CIM宏架构
(2)零消折叠ADC架构(a zerocancelling folded-ADC architecture)
下图展示了对数位宽残差ADC的工作原理和电路结构。由模拟位乘法器得到的最大模拟电流值仅为单位电流的8倍,因此该残差ADC可以通过log₂8=3位有效区分非零状态,以避免直接使用折叠ADC(Folding ADC)而导致判断如下图所示的0~8的数据时出现模糊状态。
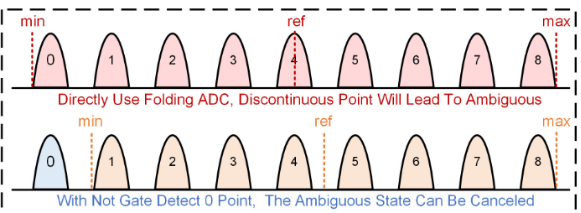
图5 零消结构对ADC的影响
即使是INT16或FP32等更高精度的需求,这种对数关系也依然成立,这极大地降低了ADC的位宽需求,从而提高计算能效。此外,减小的位宽允许更大的信号裕度,从而提高了精度。输入电流通过二极管连接的晶体管转换为电压,并被引导至两个串联的反相器,从而激活ADC。当没有电流输入时,残差ADC(Redisual ADC)会关闭以节省功耗,否则将基于残差比较原理工作。
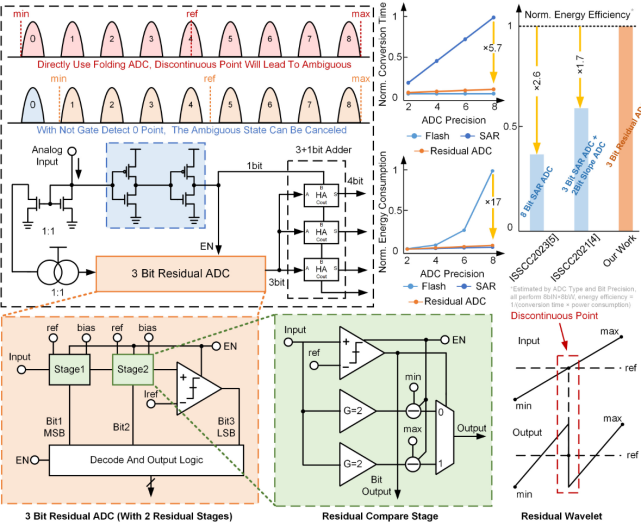
图6 本研究ADC电路结构图
该ADC架构展示了与Flash ADC相当的吞吐量,并具有与SAR ADC相当的能耗。在模拟域中执行8位输入乘8位权重操作时,3位残差ADC的能效比ISSCC2021中J.-W. Su提出的3位SAR+2位斜率ADC提高了70%,比ISSCC2023中S.-E. Hsieh提出的8位SAR ADC提高了2.6倍。
两篇对比文献的全名为ISSCC2021,J.-W. Su,A 28nm 384kb 6T-SRAM Computation-in-Memory Macro with 8b Precision for AI Edge Chips;ISSCC2023,S.-E. Hsieh,A 70.85-86.27TOPS/W PVT-Insensitive 8b Word-Wise ACIM with Post-Processing Relaxation。
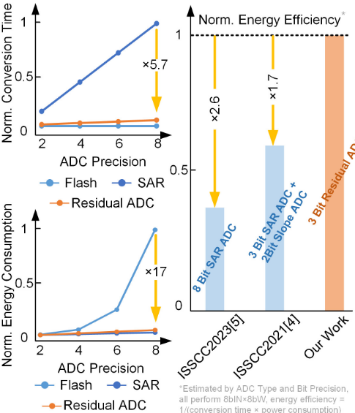
图7 本研究创新点二对比其他研究
(3)数模混合架构
论文中的Figure 34.6.5显示了基于外积的FP/INT双模CIM块的详细结构(The structure of the outer-product based FP/INT-CIM block),接下来我们对于这个架构中的每个模块分别进行分析。
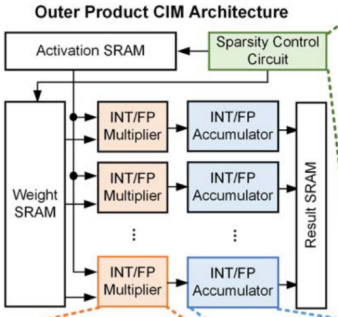
图8 Outer Product CIM Architecture
首先,论文先介绍了外积计算(Outer-Product)的原理,与传统的内积计算不同,内积需要对多个部分和的乘积进行累加。而外积架构通过直接将激活矩阵的元素(element)与权重矩阵的向量(vector)相乘来生成结果。与内积计算相比,外积计算可以避免多层复杂的加法计算,可以减少计算复杂度并改善延迟,进一步提升性能。
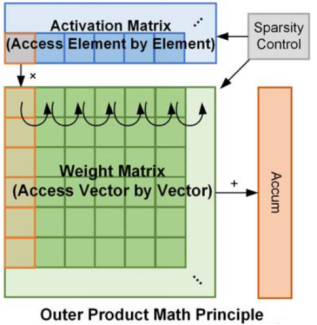
图9 Outer Product Math Principle
架构中的稀疏控制电路(Sparsity Control Circuit,绿色部分)旨在优化对于稀疏矩阵的计算效率,进一步提升能效(EF)。论文采用了压缩稀疏行(CSR Format)的数据格式来储存稀疏矩阵中的数据,索引(Indices)记录非零元素所在的列号,索引指针(Index Pointers)来记录矩阵每一行的起始位置,也即每一行第一个非零元素在索引数组中的位置。在这种数据格式的存储下,稀疏控制电路可以利用CSR格式跳过零元素的计算,先通过索引指针找到每一行的起始位置,再通过索引定位非零元素的具体位置。
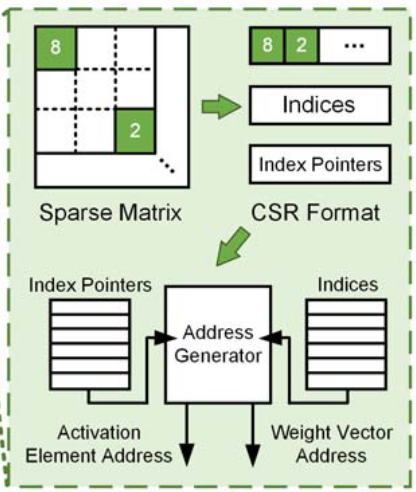
图10 Sparsity Control Circuit
架构包含可实现INT/FP双模计算的乘法器,如下图所示。在INT模式下,可以选择16比特权重存储单元的高位或低位的8比特传输到计算宏中,与1位权重值在宏中进行外积计算,此时无需调用指数&符号数计算模块(Exp&Sign Calc);在FP模式下,BF16的尾数传输至计算宏中,而符号和指数被发送到Exp&Sign Calc组件中分开计算,最终的计算结果还需要进行标准化和化整(Normalize & Round)并打包(Pack)实现BF16格式的输出。
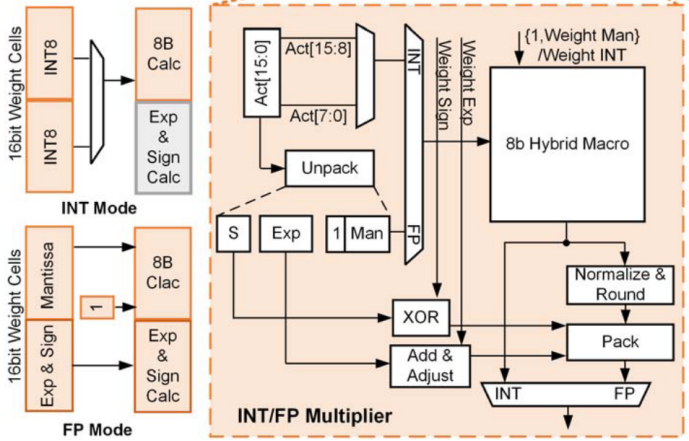
图11 INT/FP双模乘法器
架构包含可实现INT/FP双模计算的累加器,如下图所示。在INT模式下,累加器接收来自乘法器的输出结果,进行移位累加;在BF16模式下,累加器会进行指数位对齐、尾数移位并累加等操作,在累加的过程中,如果尾数位发生溢出,可能还要对指数进行进一步的调整(Exp Adjust)。
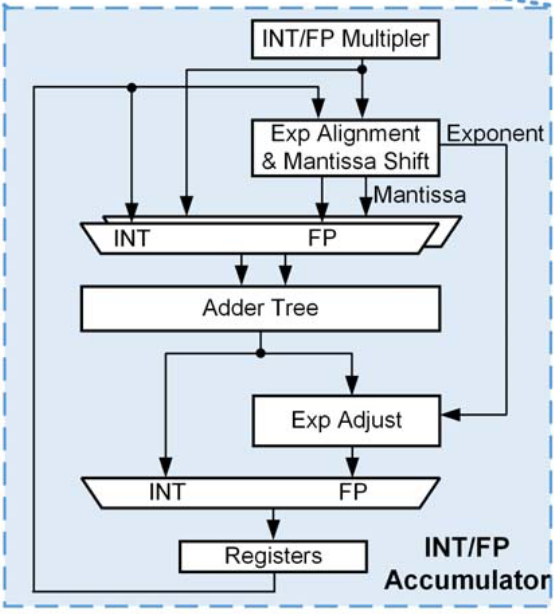
图12 INT/FP双模累加器
三、总结
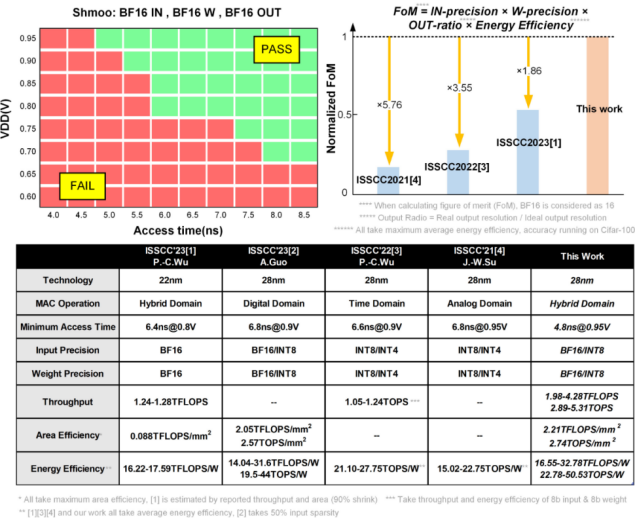
在本篇论文结尾,作者给出研究成果芯片对比其他文献的数据如下。
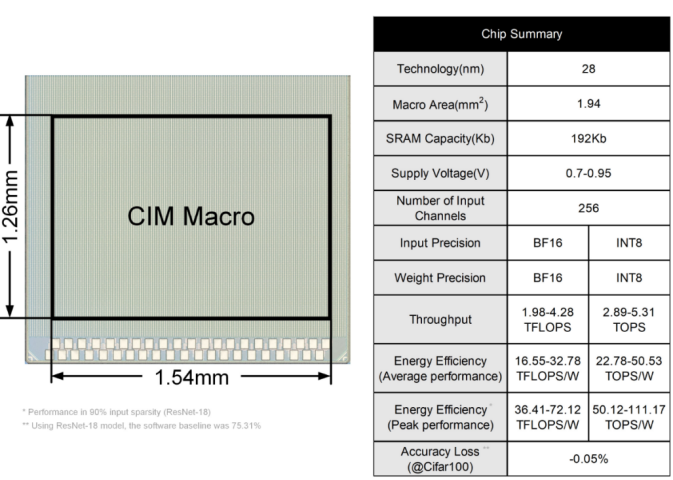
芯片图及参数总结表入下图所示。
本文提出的数模混合存内计算架构颇具特色,对比同年34.3的成果在更精细尺度上将数字和模拟存内计算范式的特色进行了结合,感兴趣的读者可以阅读我们之前对34.3文献的解析。
在零消折叠ADC架构中,作者使用了对数压缩的方式使ADC在能效、吞吐量中取得了平衡,为模拟电路设计提供了一种可能的思路和方向。
在基于外积的双模CIM架构中,文章使用了多种方法以提升能效EF,使用CSR格式存储数据以处理稀疏矩阵、执行外积运算以避免使用大扇入的多级加法器树,但是文章在进行双模计算时有着组件空闲的问题,在INT模式下,有关指数、符号数等计算组件处于空闲状态,双模情况下的硬件利用率仍是一个具有挑战性的问题。这一点在ISSCC2024 34.2中提出了一种解决办法,感兴趣的读者可以读我们之前对于34.2的解读。