MindSpore自动微分原理与实现

昇思MindSpore 2025-12-03 16:08:16

01 背景介绍

自动微分是深度学习框架的核心技术，其设计质量直接影响模型训练的效率和稳定性。MindSpore采用基于函数式编程的自动微分方案，在动态图和静态图模式下提供统一的微分接口。与基于磁带记录的自动微分方案不同，MindSpore通过源码转换和计算图构建实现微分计算，这一设计在复杂模型和高级优化场景中展现出显著优势。

本文系统分析MindSpore自动微分的技术路径，从基础原理出发，逐步深入实现细节和优化策略，为框架的深度使用和扩展开发提供理论支撑。

02 自动微分基础理论

2.1 微分计算模式比较

前向模式：基于对偶数，适用于输入维度小于输出维度的场景

反向模式：基于链式法则的反向传播，适用于深度学习中的高维输入、低维输出场景

2.2 MindSpore微分计算框架

MindSpore采用统一微分接口，支持多种微分模式：

import mindspore as ms
from mindspore import nn, ops

# 基础微分接口
class Net(nn.Cell):
    def construct(self, x):
        return x ** 2 + 3 * x + 1

net = Net()
x = ms.Tensor([2.0], requires_grad=True)

# 一阶微分
y = net(x)
grad_fn = ms.grad(net)
first_grad = grad_fn(x)  # 2*x + 3 = 7.0

# 高阶微分
second_grad_fn = ms.grad(grad_fn)
second_grad = second_grad_fn(x)  # 2.0

03 静态图模式下的自动微分实现

3.1 计算图构建与微分转换

在静态图模式下，MindSpore通过计算图分析实现自动微分：

# 计算图构建过程
def build_computational_graph(func, inputs):
    # 前向计算图构建
    forward_graph = trace_function(func, inputs)
    
    # 微分计算图生成
    grad_graph = generate_grad_graph(forward_graph)
    
    return forward_graph, grad_graph

# 微分算子生成算法
def generate_grad_graph(forward_graph):
    grad_ops = []
    
    # 反向遍历计算图
    for node in reversed(forward_graph.topological_order()):
        if node.is_leaf():
            continue
        
        # 获取节点的微分规则
        grad_rule = get_gradient_rule(node.op_type)
        
        # 生成反向微分操作
        grad_op = grad_rule(node.input_grads, node.output_grads)
        grad_ops.append(grad_op)
    return ComputationalGraph(grad_ops)

3.2 微分规则注册机制

MindSpore通过微分规则注册表实现算子的微分定义：

# 基础算子微分规则示例
@bprop_getters.register(ops.Add)
def get_bprop_add(self):
    """加法算子的反向传播规则"""
    def bprop(x, y, out, dout):
        # 加法操作的梯度传播
        dx = dout  # 对x的梯度等于输出梯度
        dy = dout  # 对y的梯度等于输出梯度
        
        # 广播梯度处理
        dx = _sum_grad(dx, x.shape)
        dy = _sum_grad(dy, y.shape)
        
        return dx, dy
    return bprop

# 复杂算子微分规则
@bprop_getters.register(ops.Conv2D)
def get_bprop_conv2d(self):
    def bprop(x, w, out, dout):
        # 卷积操作的梯度计算
        dx = ops.conv2d_backprop_input(x.shape, w, dout, 
                                      stride=self.stride, 
                                      padding=self.padding)
        dw = ops.conv2d_backprop_filter(x, w.shape, dout,
                                       stride=self.stride,
                                       padding=self.padding)
        return dx, dw
    return bprop

04 动态图模式下的即时微分

4.1 即时微分执行机制

动态图模式下，MindSpore实现即时微分计算：

class DynamicGradientEngine:
    def __init__(self):
        self.tape = GradientTape()
    
    def compute_gradient(self, func, inputs):
        # 记录前向计算
        with self.tape:
            outputs = func(*inputs)
        
        # 即时计算梯度
        gradients = self.tape.gradient(outputs, inputs)
        return gradients

# 梯度带实现
class GradientTape:
    def __enter__(self):
        self.recording = True
        self.operations = []
    
    def __exit__(self, *args):
        self.recording = False
    
    def record_operation(self, op, inputs, outputs):
        if self.recording:
            self.operations.append({
                'op': op,
                'inputs': inputs,
                'outputs': outputs
            })
    
    def gradient(self, target, sources):
        # 构建反向计算图
        grad_graph = self._build_grad_graph()
        
        # 执行梯度计算
        gradients = grad_graph.execute(target, sources)
        return gradients

4.2 高阶微分支持

MindSpore通过递归微分实现高阶导数计算：

def nth_derivative(f, n, x):
    """计算n阶导数"""
    if n == 0:
        return f(x)
    
    # 递归计算高阶微分
    def grad_func(x):
        return ms.grad(f)(x)
    
    return nth_derivative(grad_func, n-1, x)

# 应用示例：计算sin(x)的三阶导数
def f(x):
    return ops.sin(x)

x = ms.Tensor([1.0], requires_grad=True)
third_derivative = nth_derivative(f, 3, x)  # -cos(1.0)

05 性能优化技术

5.1 计算图优化策略

MindSpore应用多种图优化技术提升微分计算效率：

# 梯度计算优化
def optimize_grad_graph(graph):
    # 1. 算子融合
    graph = fuse_operations(graph)
    
    # 2. 公共子表达式消除
    graph = eliminate_common_subexpr(graph)
    
    # 3. 内存优化
    graph = optimize_memory_usage(graph)
    
    # 4. 并行化优化
    graph = parallelize_operations(graph)
    
    return graph

# 梯度检查点技术
class GradientCheckpoint:
    def __init__(self, strategy='balanced'):
        self.strategy = strategy
   
    def checkpoint_selection(self, graph):
        # 基于内存和计算代价选择检查点
        nodes = graph.nodes
        costs = self._compute_recomputation_cost(nodes)
       
        # 动态规划选择最优检查点集合
        checkpoints = self._select_optimal_checkpoints(costs)
        return checkpoints

5.2 内存优化技术

# 梯度累积优化
class GradientAccumulation:
    def __init__(self, steps=4):
        self.accumulation_steps = steps
        self.gradient_buffer = {}
    
    def accumulate_gradients(self, gradients):
        for param, grad in gradients.items():
            if param not in self.gradient_buffer:
                self.gradient_buffer[param] = grad / self.accumulation_steps
            else:
                self.gradient_buffer[param] += grad / self.accumulation_steps
        
        return self.gradient_buffer

06 实验评估

6.1 性能对比分析

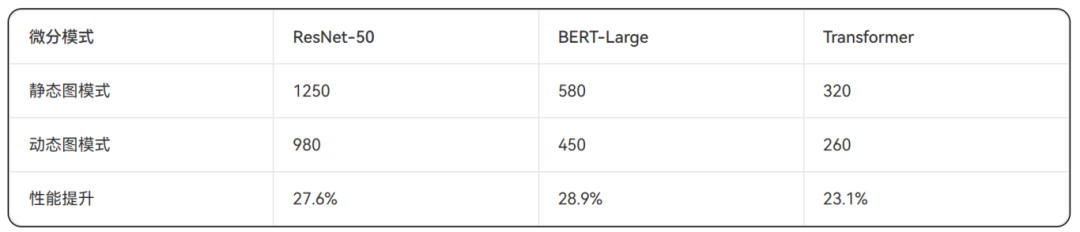
表1：自动微分模式性能对比（训练速度：samples/sec）

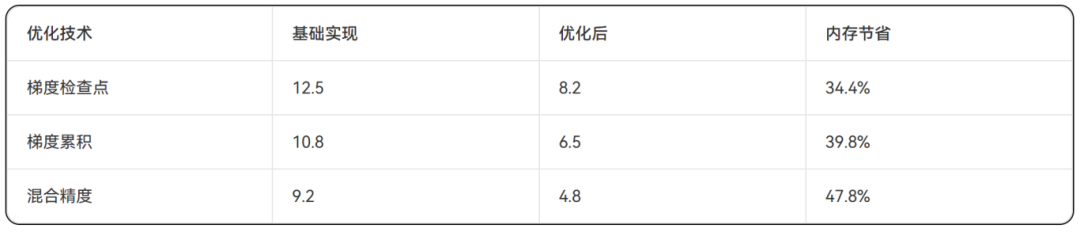
表2：内存使用效率对比（峰值内存：GB）

6.2 精度验证

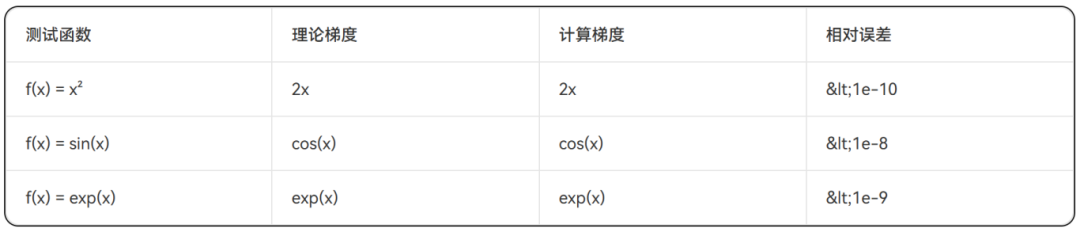
表3：自动微分数值精度验证

07 高级特性与扩展

7.1 自定义算子微分支持

# 自定义算子微分规则注册
class CustomOp(nn.Cell):
    def __init__(self):
        super().__init__()
    
    def construct(self, x):
        return custom_operation(x)

@bprop_getters.register(CustomOp)
def get_bprop_custom_op(self):
    def bprop(x, out, dout):
        # 自定义反向传播逻辑
        dx = custom_gradient_operation(x, dout)
        return (dx,)
    return bprop

7.2 微分策略扩展

# 前向模式自动微分
class ForwardModeAD:
    def __init__(self, primal_func):
        self.primal_func = primal_func
    
    def jacobian(self, x):
        # 前向模式计算雅可比矩阵
        jac = []
        for i in range(x.size):
            # 对每个输入维度计算导数
            x_dual = make_dual(x, i)
            y_dual = self.primal_func(x_dual)
            jac_col = get_dual_part(y_dual)
            jac.append(jac_col)
        return ops.stack(jac, axis=1)